Тензор леві-чевіта.
Тензор
Леві-Чевіта:
,
якщо i, j, k
створюють
парну перестановку;
,
якщо i, j, k
створюють
непарну перестановку;
,
якщо хоча б два індекси співпадають.
З допомогою тензора Леві-Чевіта можна визначити компоненти векторного добутку
.
.
Знайти компоненти Cx, Cy, Cz векторного добутку , а також подвійного векторного добутку
,
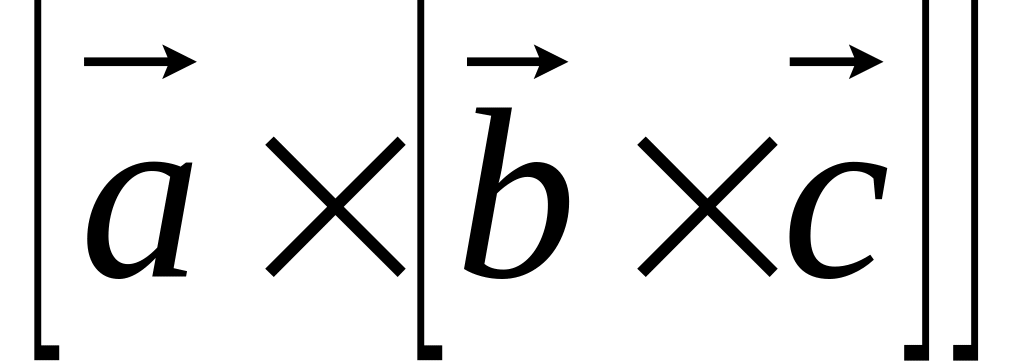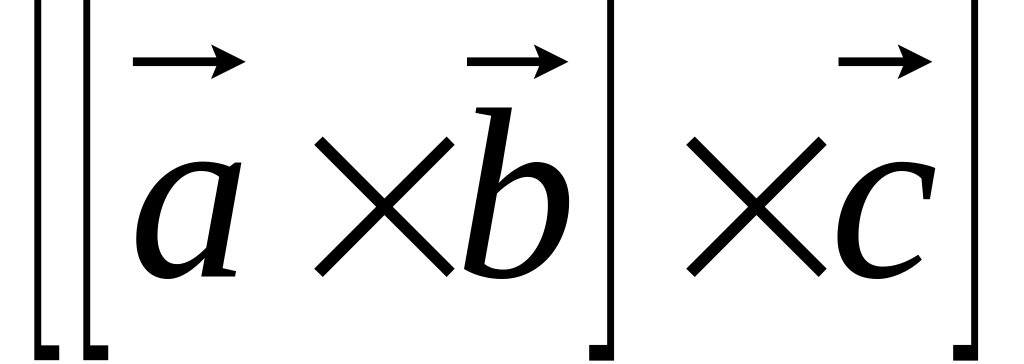(використовуючи вектор Леві-Чевіта).
Розв’язання.
.
Визначити зміну напрямку розповсюдження світла при переході із однієї інерціальної системи координат в іншу. Системи рухаються одна відносно одної із швидкістю
вздовж осі 0х.
Розв’язання.
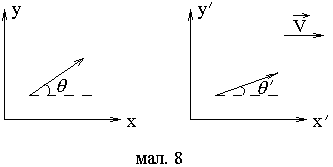
Згідно
з законом додавання швидкостей, швидкість
частинки в новій системі координат (
)
пов’язана з швидкістю частинки в старій
системі координат (
)
співвідношенням:
;
;
;
;
;
.
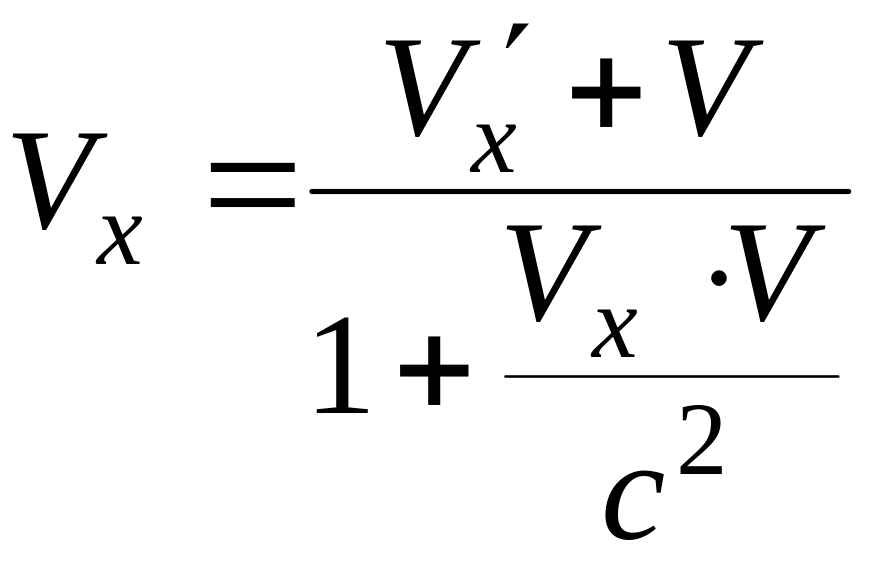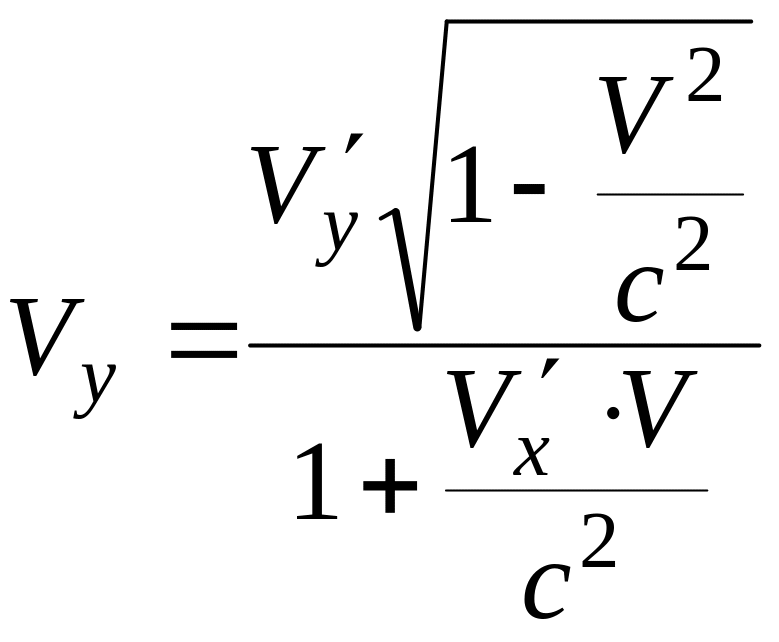Тоді:
;
;
.
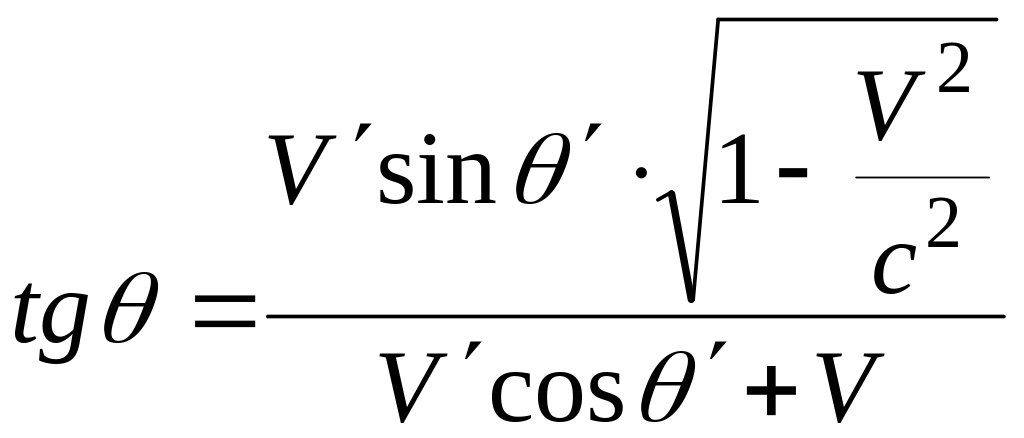Швидкість
світла однакова у всіх системах відліку
.
;
;
.
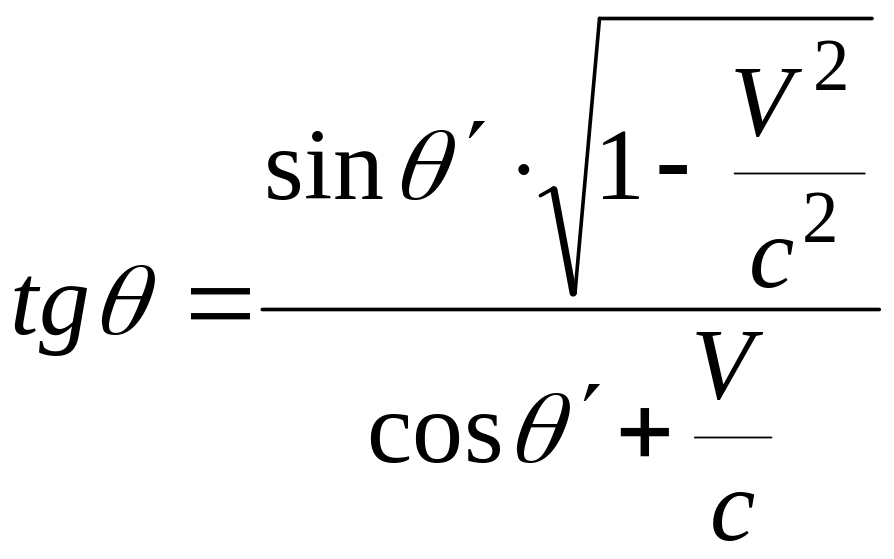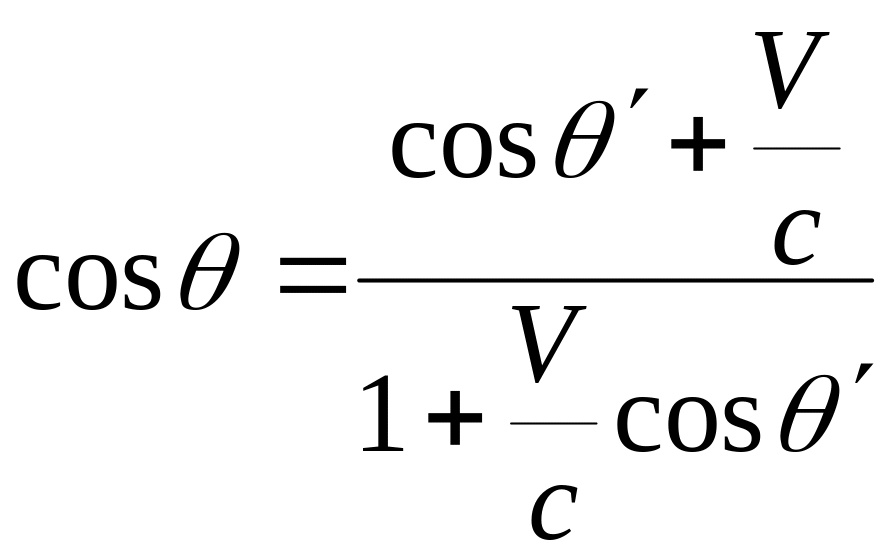Розглянемо
випадок
.
Тоді з точністю до членів, які лінійні
по
.
Введемо
кут аберації
.
Використовуючи
тригонометричні співвідношення,
отримаємо:
.
.
Використовуючи інтегральні рівняння Максвела знайти напруженість електричного поля, яке створюється однорідно зарядженою кулею з густиною зарядів ρ і радіусом R.
.
Розв’язання.
Досліджуване розподілення заряду має сферичну симетрію, тому створюване ним поле таж має таку симетрію. Виберемо сферичну систему координат з початком у центрі кулі.
Вектор
напруженості поля має вигляд
,
але із-за симетричного розподілу зарядів
.
Використаємо рівняння:
,
за поверхню інтегрування S виберемо поверхню кулі.
.
.
Так
як
і не залежить від θ
і φ,
то
.
,
де інтегрування ведеться по об’єму
кулі.
Тоді
З
допомогою вибраного рівняння Максвела
можна знайти лише
.
Для знаходження
і
необхідно використати рівняння
,
або в компонентах
.
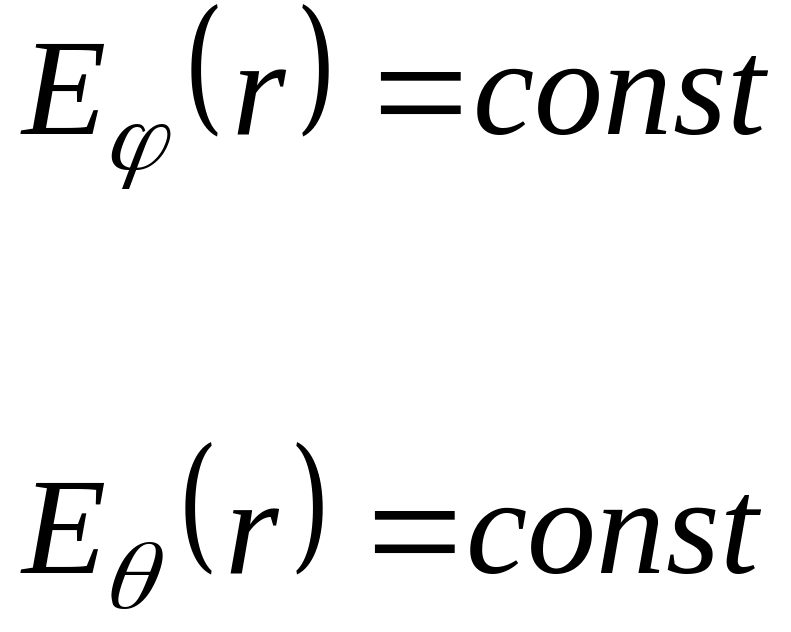Якщо
,
то поле не задовольняє умовам симетрії,
так як зафіксований напрямок стає
виділеним.
Таким
чином
;
.
.
Розглянути провідник, у якому додатні заряди рухаються вправо із швидкістю V0, а з від’ємним зарядом вліво з швидкістю V0. Лінійна густина зарядів в лабораторній системі λ. Паралельно провідникові рухається точковий заряд q із швидкістю V вправо. Знайти силу взаємодії точкового заряду з провідником в системі відліку, пов’язаною з рухомим зарядом.
Розв’язання.
В системі відліку, яка пов’язана з рухомим зарядом, заряд знаходиться в стані спокою, тому маємо задачу про взаємодію нерухомого заряду з зарядженим провідником.
В лабораторній системі провідник електронейтральний (так як густини від’ємних і додатних зарядів однакові), а в системі, яка пов’язана з точковим зарядом, умова електронейтральності порушується.
Для того, щоб знайти силу взаємодії визначимо густини зарядів q+ і q- в системі відліку, яка пов’язана з зарядом. Знайдемо швидкості руху цих зарядів в даній системі
;
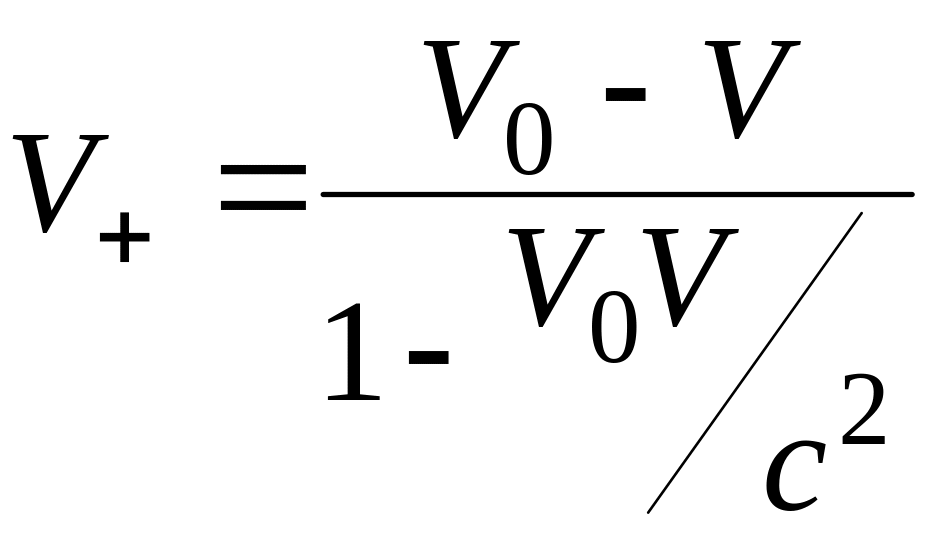Введемо коефіцієнти β+, γ+, β0 , γ0 , β- , γ- , β, γ наступним чином:
;
;
;
;
;
.
Знайдемо
густини зарядів
і
в новій системі відліку. Зміна густини
зарядів обумовлена Лоренцевим скороченням.
Густина зарядів Q/l,
де Q-
величина заряду, l-
довжина провідника. Густина зарядів в
лабораторній системі координат дорівнює
λ, тоді у власних системах відліку
;
.
В системі відліку, яка пов’язана з рухомим зарядом
;
.
Повна густина зарядів
;
;
.
Напруженість електричного поля, яке створюється однорідно зарядженою ниткою, дорівнює
.
Сила:
,
(
).
В лабораторній системі
-
сила струму в провіднику.
