5. Построение зависимостей спроса, дохода, прибыли и коэффициента эластичности от цены

Во всех расчетах этого пункта будем использовать теоретические значения спроса

• Еще раз скопировать исходные данные для цены на этот раз в столбец BI.

• В столбец BJ так же скопировать теоретические значения спроса.

• В столбце BL подсчитать коэффициент эластичности по формуле

Знаменатель можно не программировать, а использовать столбец теоретиче-

ских значений спроса.

• В столбце BN подсчитать величину дохода: Z = P ^ D(P).

• В ячейки BP23 и BP24 занести значения постоянных затрат C и переменных затрат V из вашего варианта исходных данных (дать ячейкам имена).

• В столбце BO подсчитать издержки: G =C + VD.

• В столбце BP подсчитать прибыль: F =Z – G.

• Построить графики полученных зависимостей (Мастер диаграмм, Точечная диаграмма с последующим редактированием):

• Зависимость коэффициента эластичности от цены.

Использовать столбцы BI, BL и клавишу Ctrl.

• На одном графике совместить зависимость дохода, издержек и прибыли от цены.

Использовать столбцы BI, BN, BO, BP и клавишу Ctrl. Отредактиро-

вать график, чтобы он выглядел следующим образом:

6. Расчет оптимальной цены при которой будут максимальными доход или прибыль

• Доход:

• В ячейках CC11:CE11 по коэффициентам регрессии находим коэффициенты квадратного уравнения для оптимальной цены.

• В ячейке CF11 подсчитаем дискриминант.

• В ячейках CC14:CD14 программируем известную формулу для корней квадратного уравнения.

• Ориентируясь на уже построенный график, выбираем из корней нужный и заносим его в ячейку CF.

• Прибыль:

• Совершенно аналогично находим оптимальную цену по прибыли. Используем соответствующие ячейки 11 и 14 строки.

7. Расчет оптимальных значений спроса , дохода и прибыли

• В ячейку CF21 заносим оптимальную цену (по прибыли).

• В остальных ячейках этого столбца подсчитываем по соответствующим формулам остальные величины.

8. Доверительные интервалы для оптимальных значений спроса , дохода и прибыли

• В ячейки CH21:CJ21 заносим последовательно: 1; оптимальную цену; квадрат оптимальной цены . Выделяем все три ячейки и присваиваем этому массиву имя (например Xp). Таким образом, получаем матрицу- cтроку Xp.

• В ячейку CM21 помещаем взятое из таблиц Стьюдента значение коэффициента . Даем имя (tg).

• В ячейку CM22 заносим стандартное отклонение остатков S_ост .

• В ячейке CM20 подсчитываем размах доверительного интервала для спроса, соответствующего оптимальной цене.

• Используем расчетную матричную формулу :

- это только что сформированный массив Xp

- трехстолбцовый массив, содержащийся в столбцах AI, AJ, AK. Он использовался при построении матрицы нормальной системы и уже имеет имя Xmatr.

• Программируем в ячейке CI22 матричную формулу, стоящую под корнем:

=1+МУМНОЖ(МУМНОЖ(Xp;МОБР(МУМНОЖ(ТРАНСП(Xmatr); Xmatr)));ТРАНП(Xp))

Завершаем ввод формулы сочетанием клавиш

• В ячейке CM20 программируем выражение для доверительного интервала = tg*S_ост*КОРЕНЬ(CI22).

• В ячейках CJ24 и CL24 к значению Dopt из ячейки CF24 прибавляем и вычитаем найденное .

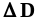• По найденным границам доверительного интервала для D пересчитываем границы доверительных интервалов для остальных величин - дохода Z=P∙D и прибыли F= Z - (V+C∙D).

Сохранить файл в своей личной папке:

Сохранить файл на дискете.

Исходные данные к лабораторной работе