27

Лабораторный практикум.

ИНСТРУКЦИЯ К ЛАБОРАТОРОЙ РАБОТЕ

Анализ монопольного рынка

Введение

Имеются статистические данные для цены P и для спроса D на монопольный товар. Требуется рассчитать оптимальные цены, при которых

будут максимальными доход или прибыль.

Если описать зависимость спроса D от цены P теоретической формулой D(P), то с помощью этой теоретической зависимости можно будет исследовать зависимость дохода Z и прибыли F от цены P .

Примем квадратичную зависимость D(P):

D(P) =a ₂·P ² + a ₁·P + a ₀

Тогда величина дохода Z равна произведению цены P на объем реализованного спроса:

Z = P·D(P) = a ₂·P ³ + a ₁·P ² + a ₀·P .

Прибыль F от реализации товара равна разности дохода Z и издержек G:

F = Z – G

В свою очередь, издержки G состоят из постоянных (C) и переменных затрат (V·D), которые пропорциональны объему произведенной продукции (V – затраты на единицу продукции):

G = C + V · D.

Таким образом, для прибыли получаем формулу:

F = P·D(P) - [C+V·D(P)] = a ₂·P ³ + (a ₁ -Va ₂) ·P ² + (a ₀ - Va ₁) · P + (–C – Va ₀)

Чтобы найти величину цены, при которой максимальны доход или прибыль, нужно взять производную от них по цене P приравнять ее нулю:

и

Решая эти квадратные уравнения и выбирая из двух корней то значение, которое соответствует максимуму, находим значение цены, при которой максимальны доход или прибыль.

Рассмотрим также величину, называемую коэффициентом эластичности спроса:

.

Это число показывает, на сколько процентов изменяется спрос D при росте цены на 1% .

Так как цена P и спрос D всегда положительны, знак K _d определяется знаком производной. Для подавляющего большинства товаров спрос падает с ростом цены, и значит производная D^′_p отрицательна. А значит, отрицательным будет и коэффициент эластичности.

Существует такое понятие, как эластичность и неэластичность спроса. При этом характер спроса определяется реакцией дохода на изменение цены.

О пределение:

• спрос неэластичен, если с ростом цены доход тоже растет;

• спрос эластичен, если с ростом цены доход убывает.

Рост или убывание дохода определяется знаком производной :

В зависимости от величины коэффициента эластичности K _d

возможны следующие случаи:

1. . Производная > 0  с ростом цены несмотря на

снижение спроса доход продолжает расти. Спрос неэластичен.

2. . Производная < 0  с ростом цены доход падает.

Спрос эластичен.

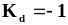3. . Производная = 0  Доход максимален.

Для выполнения работы необходимо :

1. Построить по имеющимся статистическим данным корреляционное

поле и найти выборочные числовые характеристики.

2. Составить нормальную систему уравнений для определения

коэффициентов параболической регрессии.

3. Решить систему и записать уравнения зависимости спроса от цены.

4. Проверить адекватность построенной корреляционной модели.

5. Построить зависимости спроса, дохода, прибыли и

коэффициента эластичности от цены.

6. Рассчитать оптимальную цену, при которой будут максимальными

доход или прибыль.

7. Для цены, обеспечивающей максимальную прибыль, рассчитать

соответствующие значения спроса, дохода и прибыли.

8. Найти доверительные интервалы для оптимальных значений этих

величин.

• В папке “трафареты” найти файл « л р № 2 трафарет. Xls ».

• Скопировать его в свою папку « Группа ***» и переименовать, вставив вместо слова “трафарет” свою фамилию: «Л.Р. № 2 Фамилия »

• Только после этого открыть файл и приступить к работе

1. Корреляционное поле и выборочные числовые характеристики.

• Из таблицы исходных данных выбрать свой номер варианта. Столбец цен P у всех один и тот же, столбец спроса D – выбирается по номеру варианта.

• Занести исходные данные (выборку) в отведенные ячейки: (столбцы N, O). Каждому из этих столбцов дать имя, напр. P,D ).

• По исходным данным построить корреляционное поле с помощью «Мастера диаграмм», «Точечная диаграмма».

• По выборке найти ее объем n (ячейка O23)

(функция СЧЕТ). Ячейке присвоить имя (например "объем" или n).

• в отведенных для этого ячейках 25, 27 и 30 строк подсчитать числовые характеристики факторов P и D:

• средние (СРЗНАЧ)

• дисперсии (диспр)

• стандартные отклонения ( )

ячейкам присвоить соответствующие имена (Напр. Pср, Dср; Dp, Dd; Sp, Sd).

2. Нормальная система уравнений для коэффициентов параболической регрессии

• Уравнение параболической регрессии имеет вид . Для коэффициентов составляется нормальная система линейных уравнений с матрицей

Для заполнения этой матрицы используем два способа.