4. Стаціонарні і квазістаціонарні струми і магнітні поля

Рівняння Максвела мають вигляд

, ,

де - магнітна індукція, - напруженість магнітного поля, - густина об’ємного струму.

де - магнітна проникливість середовища.

Елемент струму створює в вакуумі, або однорідному середовищі магнітне поле

.

Граничні умови для векторів і на межі двох областей 1 і 2

, ,

де - нормаль до межі розділу областей, - густина поверхневого струму.

Магнітне поле можна задати за допомогою векторного потенціалу

.

З додатковою умовою

.

В однорідних магнетиках

.

Енергія магнітного поля, яка локалізована усередині об’єму V виражається

.

ЗАДАЧІ

158. Сферичний заземлювач радіусом знаходиться в середовищі з відносно невеликою провідністю γ. До нього підводиться струм I. Визначити опір розтікання. Заземлювач, заритий на глибину, яка набагато більша від його радіуса.

159. Плоский конденсатор з двошаровим діелектриком вмикається на постійну напругу U. Товщини шарів діелектрика, їх діелектричні проникливості та питома провідності постійні та відповідно рівні 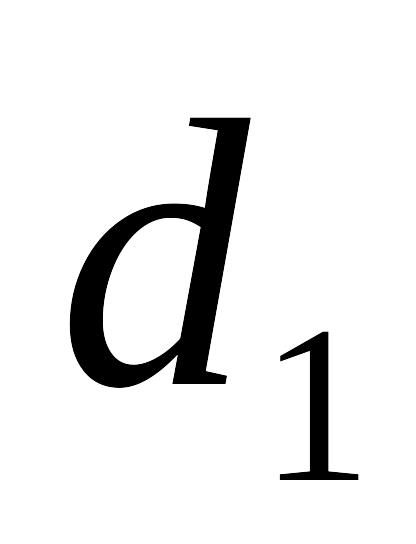, , 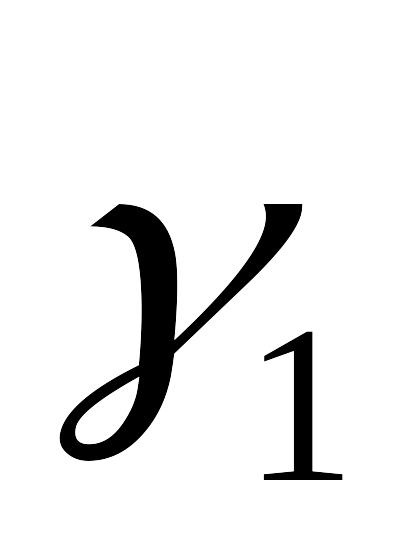та 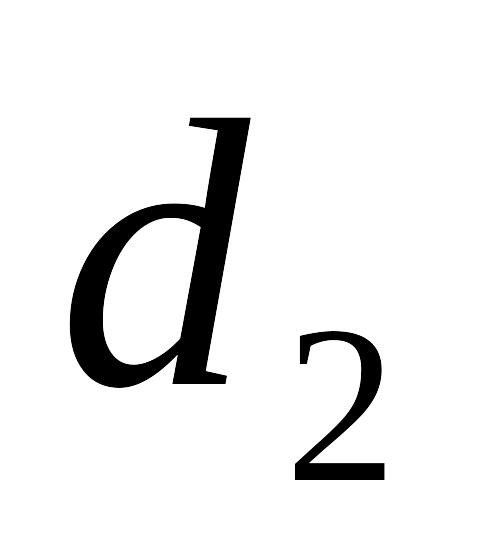, , 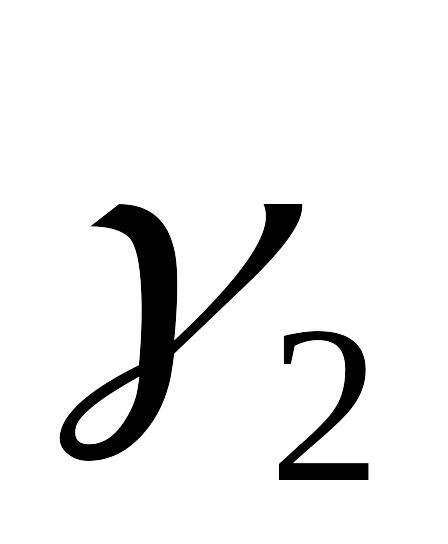. Вивести загальне рівняння зміни в часі напруженостей електричного поля в кожному шарі.

160. Між обкладками сферичного конденсатора з радіусами і 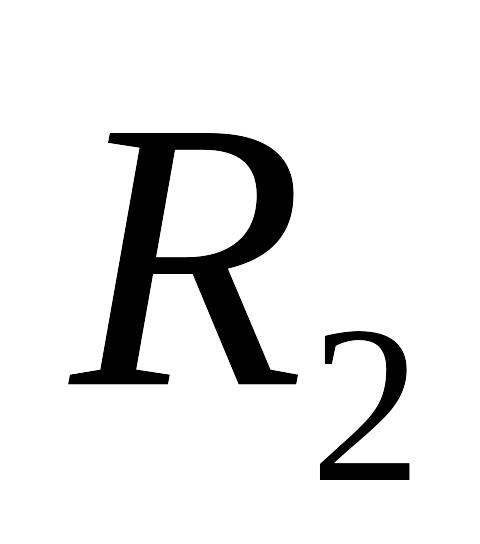підтримується постійна різниця потенціалів U. Простір між обкладками заповнений однорідним середовищем з питомою провідністю σ. Знайти опір між обкладками, силу струму та потужність теплових втрат.

161. Знайти опір заземлення між двома електродами з ємностями і , якщо вони зариті в землю на велику глибину і знаходяться на великій відстані. Питома провідність землі біля електродів і .

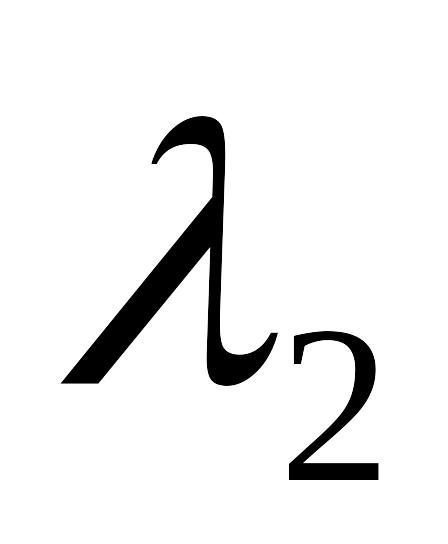162. Знайти напруженість магнітного поля, яке створюється в вакуумі тонким прямолінійним провідником довжиною 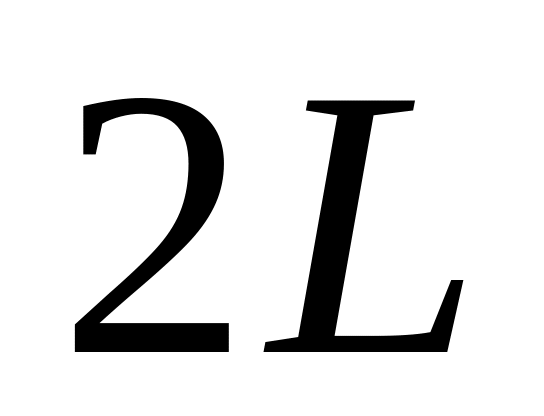. Сила струму в провіднику I. Розглянути випадок, коли → ∞.

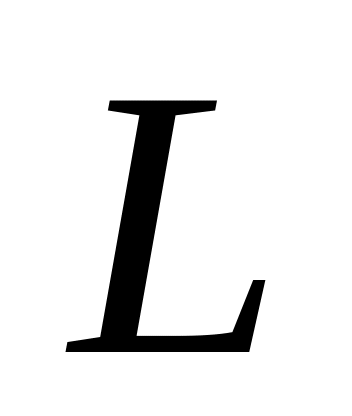163. Визначити магнітні силові лінії поля, розглянутого в попередній задачі.

164. Знайти напруженість магнітного поля на вісі кільцевого струму радіусом 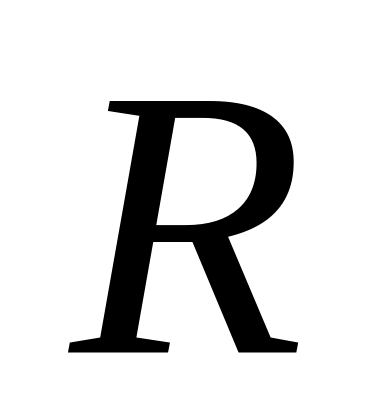та силою струму I.

165. Визначити векторний потенціал магнітного поля, яке створюється в вакуумі прямолінійним струмом I довжиною . Розглянути випадок, коли →∞.

166. Знайти потенціал та напруженість магнітного поля, яке створюється струмом I, який рівномірно розподілений по перетину нескінченно довгого циліндричного провідника радіусом . Магнітна проникливість середовища 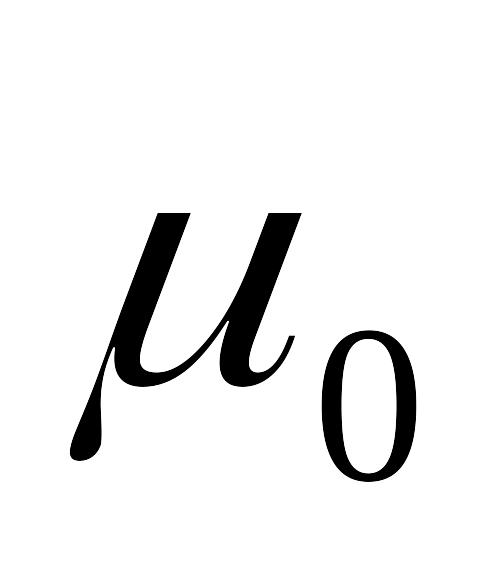, провідника - .

167. Струм I проходить по нескінченному провіднику у формі порожнього циліндру з зовнішнім та внутрішнім радіусами a і b відповідно. Магнітна проникливість провідника , середовища - . Визначити векторний потенціал та напруженість магнітного поля.

168. Вивести рівняння для напруженості магнітного поля і векторного потенціалу в коаксіальному кабелі шляхом інтегрування рівнянь Пуассона–Лапласа для векторного потенціалу. Радіус внутрішнього провідника , зовнішнього і 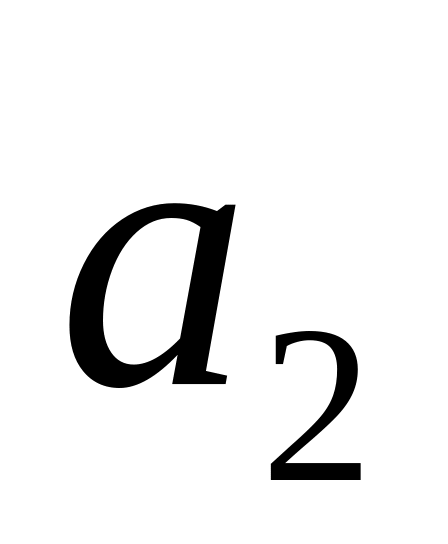відповідно ( ).

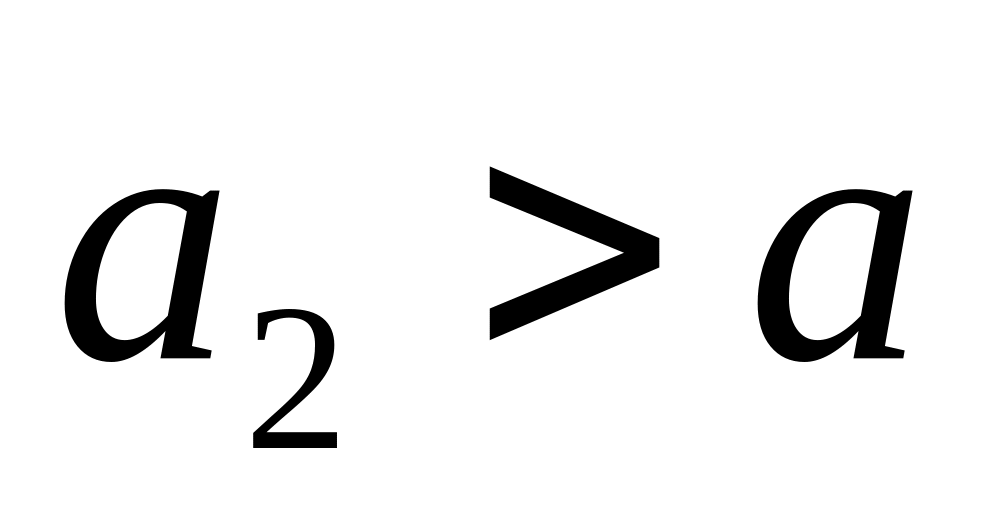169. В однорідне магнітне поле з напруженістю 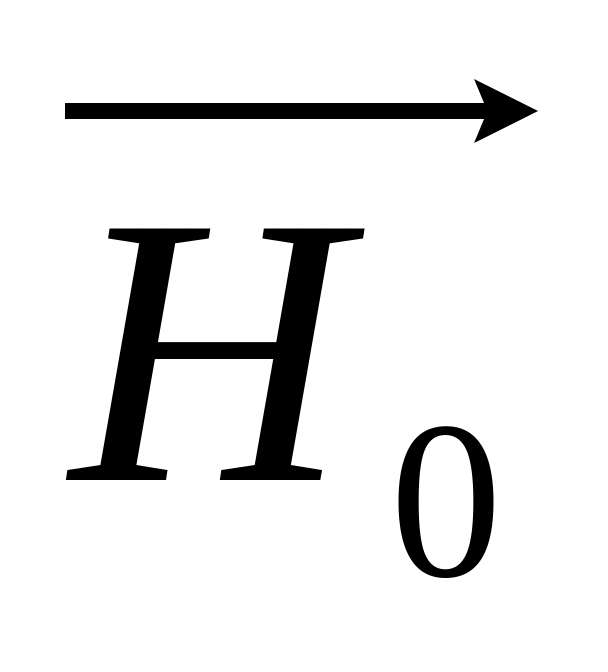внесли круглий прямий циліндр з радіусом так, що його вісь перпендикулярна вектору . Магнітна проникливість матеріалу циліндра , навколишнього середовища . Визначити поле всередині та зовні циліндра. Краєві ефекти не враховувати.

170. В однорідне магнітне поле з напруженістю внесли кулю радіусом а. Магнітна проникливість кулі , навколишнього середовища . Визначити поле всередині та зовні кулі.

171. По тонкій проволоці у вигляді тонкого кільця з радіусом , тече постійний струм I. Визначити векторний потенціал та напруженість магнітного поля в точці, яка знаходиться на відстані l від кільця не на його вісі (l>>a).

172. По нескінченно довгому циліндричному провіднику з радіусом а проходить струм I, який рівномірно розподілений по площі поперечного перетину. Знайти за допомогою рівнянь Максвела напруженість поля, яке створюється цим струмом в однорідному середовищі.

173. На залізний тор з магнітною проникливістю , намотано густо і рівномірно N витків тонкої ізольованої проволоки, по якій тече струм I. Визначити напруженість магнітного поля всередині тора.

174. Однорідна немагнітна куля ( 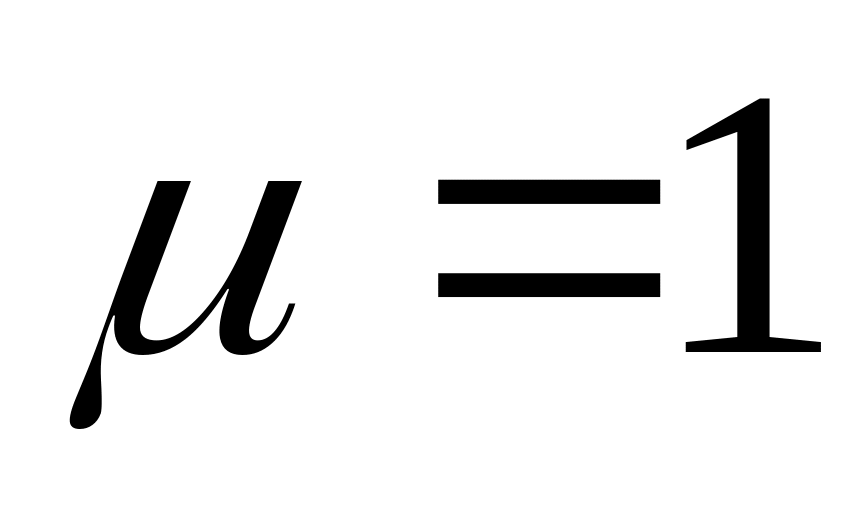) радіусом рівномірно заряджена по об’єму. Куля обертається з кутовою швидкістю навколо осі, яка проходить через центр кулі. Заряд кулі q. Визначити магнітний момент кулі.

175. Немагнітний циліндр ( ) радіусом a і висотою h рівномірно заряджений по об’єму і обертається навколо своєї геометричної вісі з кутовою швидкістю ω. Заряд циліндра q. Визначити магнітний момент циліндра.

176. Знайти силу взаємодії в повітрі між двома паралельними нескінченними прямолінійними струмами силою 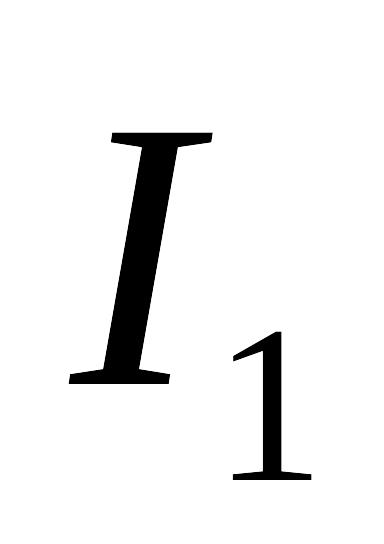і 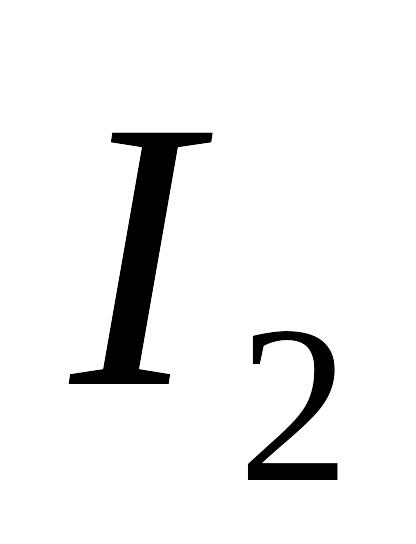. Відстань між ними 2a.

177. Розв’язати попередню задачу за допомогою тензора натягу Максвела.

178. Визначити самоіндукцію одиниці довжини нескінченної круглої котушки з радіусом a. Число витків на одиницю довжини n; магнітна проникливість сердечника .

179. Визначити рух нерелятивістського електрона в однорідному магнітному полі з напруженістю . Початкова швидкість електрона 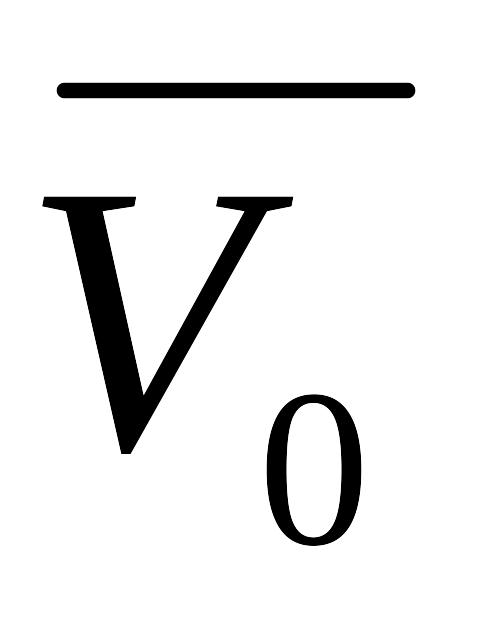складає кут з напрямком поля.

180. Плоский контур обертається кутовою швидкістю в однорідному магнітному полі навколо вісі, яка перпендикулярна полю. Індукція поля . Визначити електрорушійну силу в контурі. Площа контуру .

181. Визначити силу струму в контурі із попередньої задачі. Самоіндукція контуру , опір .

182. Заряджений конденсатор з ємністю 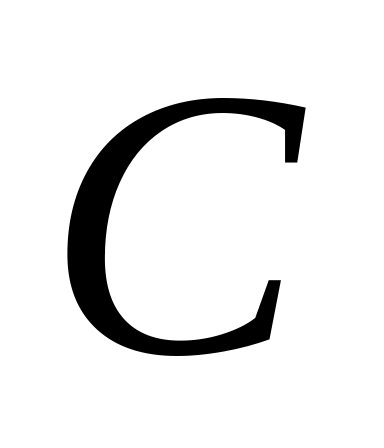замкнутий на опір з самоіндукцією . Визначити заряд на обкладках конденсатора як функцію часу. Початковий заряд .

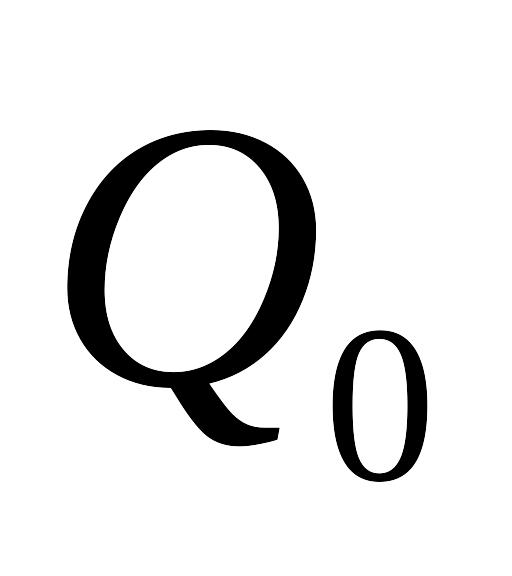183. Батарея з е.р.с. і внутрішнім опором , конденсатор з ємністю і котушка з індуктивністю з’єднані паралельно. Визначити силу струму в батареї після замикання. Опором котушки і проводів з’єднання знехтувати.

184. Визначити магнітне поле в циліндричному отворі в нескінченно довгому циліндричному провіднику, по якому тече струм рівномірно розподілений по його перерізу.

185. Знайти активний опір тонкого циліндричного провідника для випадку скін-ефекту. Довжина провідника , радіус , провідність , магнітна проникливість μ. Дослідити випадки великих та малих частот.

186. Стержень ОА обертається з кутовою швидкістю навколо точки О в площині, яка перпендикулярна до напрямку однорідного магнітного поля . Визначити е. р. с. індукції між точками О і А, якщо довжина стержня .