3. Постійне електричне поле

Напруженість електричного поля задовольняє рівнянням Максвелла:

; .

Електростатична теорема Гаусса:

Напруженість і потенціал електричного поля пов’язані співвідношенням:

Потенціал задовольняє рівнянню Пуассона:

На зарядженій поверхні, яка розділяє дві області 1 і 2

Нормаль направлена з області 1 в область 2, - поверхнева густина зарядів.

Енергія електростатичного поля

;

ЗАДАЧІ

Знайти за допомогою закону Кулона потенціал і напруженість поля в вакуумі, яке створюється нескінченною прямолінійною ниткою, рівномірно зарядженою з лінійною густиною .
Знайти за допомогою закону Кулона потенціал і напруженість поля в вакуумі, яке створюється нескінченною площиною, рівномірно зарядженою з поверхневою густиною .
Знайти за допомогою закону Кулона потенціал і напруженість поля в вакуумі, яке створюється нескінченним круглим циліндром, рівномірно зарядженим з лінійною густиною . Радіус циліндра R.
Поле створюється в вакуумі рівномірно зарядженим колом радіусом R і зарядом Q. Знайти потенціал та напруженість поля на осі кола.
Знайти потенціал та напруженість електричного поля кулі , яка рівномірно заряджена по об’єму. Радіус кулі R, заряд q. Діелектрична проникливість навколишнього середовища .
Знайти потенціал та напруженість електричного поля сфери, яка рівномірно заряджена по поверхні. Заряд сфери q. Діелектрична проникливість навколишнього середовища .
Визначити за допомогою теореми Остроградського-Гаусса поле, яке створюється рівномірно зарядженою поверхнею нескінченного циліндра радіусом R в діелектричному середовищі з проникливістю . Поверхнева густина зарядів =const.
Визначити за допомогою теореми Остроградського-Гаусса поле, яке створюється нескінченною рівномірно зарядженою площиною (=const), по обидві сторони якої простір, заповнений однорідним діелектриком з проникливістю .
Знайти потенціал поля, яке створюється в вакуумі прямолінійним рівномірно зарядженим відрізком довжиною 2l і лінійною густиною зарядів . Визначити еквіпотенціальні поверхні цього поля.
Потенціал електростатичного поля в вакуумі

Визначити якою системою електричних зарядів створюється це поле.

Потенціал поля в вакуумі

R₀ і a - постійні. R - відстань до вісі. Визначити відповідний розподіл зарядів.

Потенціал поля в вакуумі

r-відстань до початку системи координат, q і a – постійні. Визначити відповідний розподіл зарядів.

За допомогою рівняння Лапласа визначити потенціал поля, яке створюється в вакуумі рівномірно зарядженою нескінченно довгою поверхнею круглого циліндра радіуса R. Знайти напруженість цього поля.
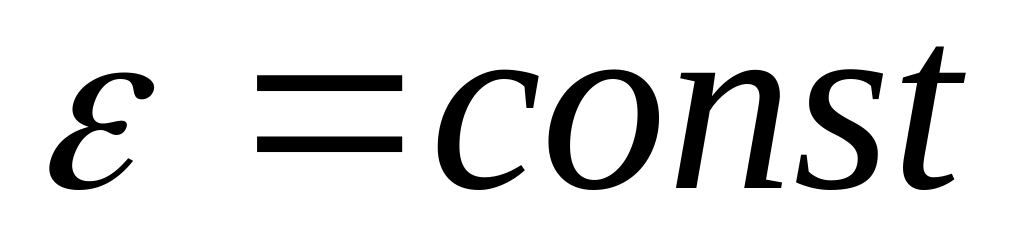За допомогою рівняння Пуассона визначити потенціал та напруженість поля, яке створюється нескінченним плоским шаром товщиною ₂_a, який рівномірно заряджений з об’ємною густиною . Діелектрична проникливість . Навколишнє середовище – вакуум.
За допомогою рівняння Пуассона визначити потенціал та напруженість поля, яке створюється кулею радіусом R рівномірно зарядженою з об’ємною густиною . Діелектрична проникливість . Навколишнє середовище – вакуум.
За допомогою рівняння Пуассона визначити потенціал та напруженість поля, яке створюється однорідним нескінченним круглим циліндром радіусом R рівномірно зарядженим з об’ємною густиною . Діелектрична проникливість циліндра . Навколишнє середовище – вакуум.
Площина xy несе заряд неперіодичною поверхневою густиною 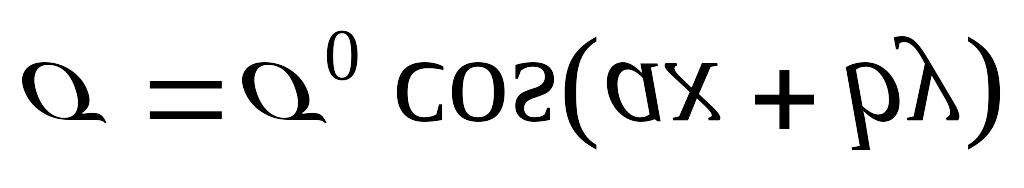. Знайти потенціал  електричного поля в необмеженому просторі.
Заряд, розподілений в просторі по неперіодичному закону 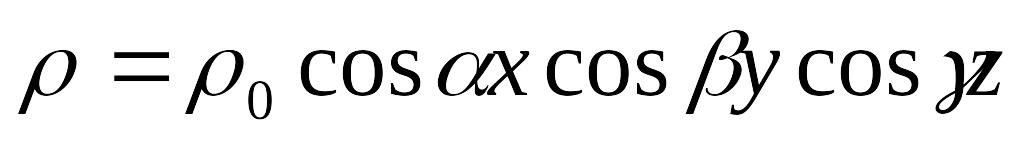, створює нескінченну просторову неперіо-дичну систему. Знайти потенціал електричного поля.
В однорідне електростатичне поле з напруженістю 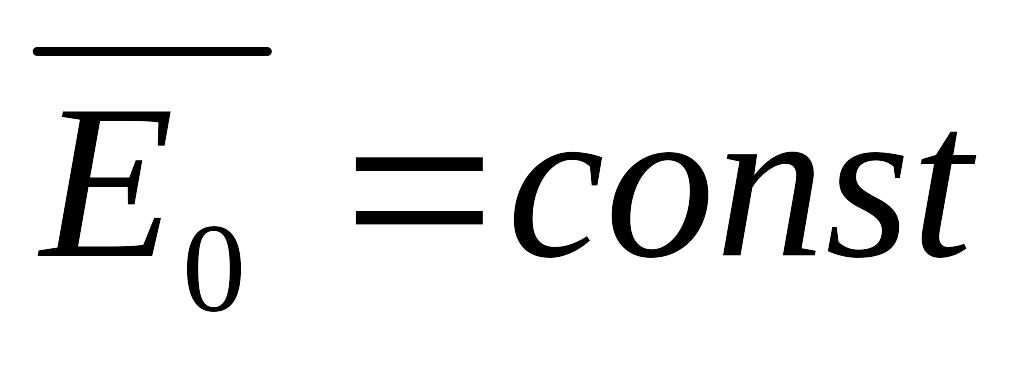внесли металеву кулю радіусом R. Діелектрична проникливість середовища .
В однорідне електричне поле з напруженістю 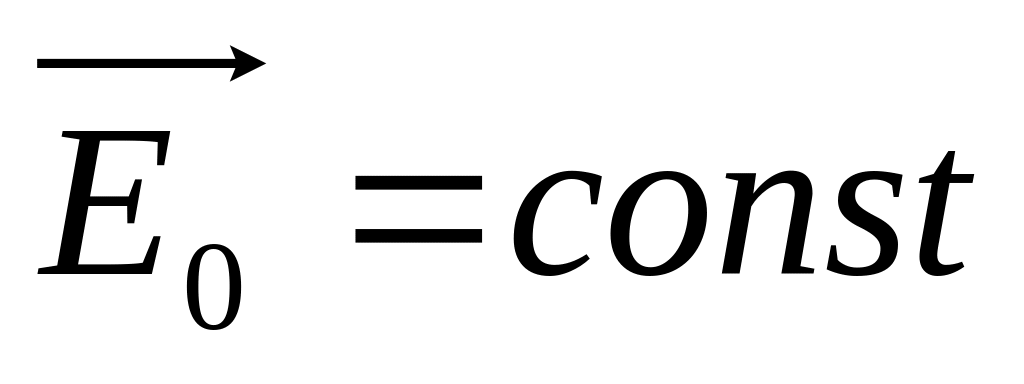внесли однорідний нескінченно довгий провідник у формі циліндра радіусом R. Вісь циліндра перпендикулярна полю. Визначити поле навколо циліндра.
Визначити поле навколо точкового заряду q, який розташований на відстані h від плоскої межі розподілу двох різних середовищ.
Точковий заряд q знаходиться на відстані h від нескінченної плоскої поверхні провідника. Знайти потенціал електричного поля та густину заряду на поверхні провідника.
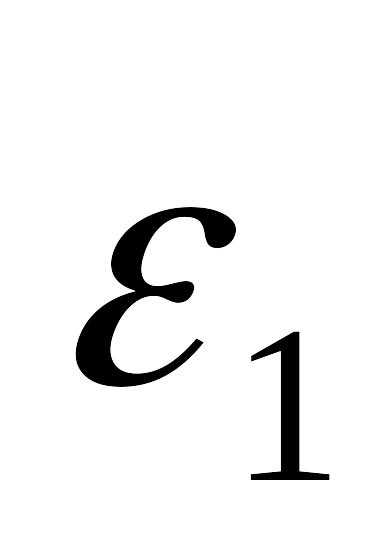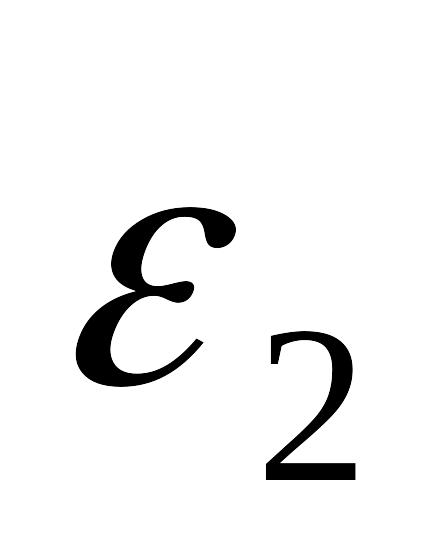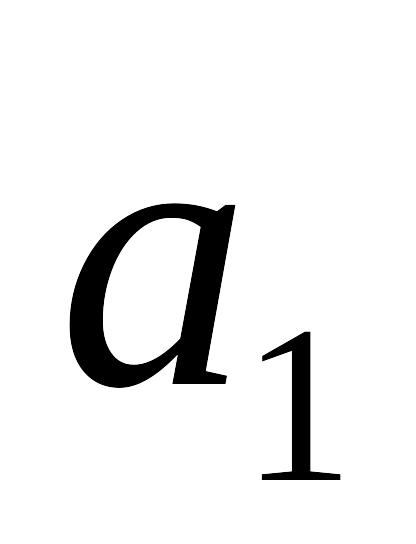Дослідити поле циліндричного конденсатора довжиною l , який складається з двох шарів та визначити його ємність. Діелектрична проникливість внутрішнього шару , зовнішнього - . Радіуси шарів і 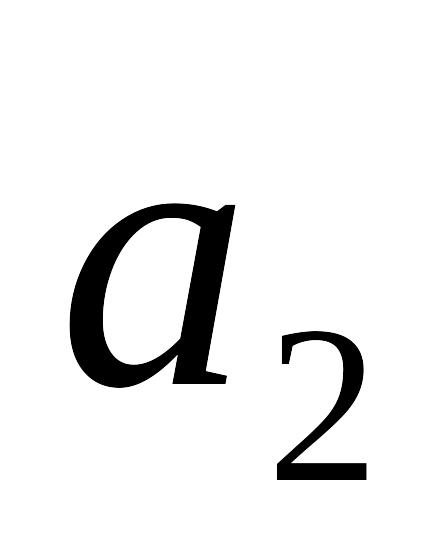відповідно. Заряд конденсатора Q.
Навколо кулі із провідника радіусом a знаходиться концентричний шар діелектрика радіусом _b. Знайти ємність конденсатора, якщо проникливість середовища .
Знайти ємність плоского конденсатора. Площа поверхні обкладок S, між ними два плоскопаралельних шари однорідних діелектриків з проникливостями та відповідно. Товщина першого шару d₁, другого –d₂. Краєві ефекти не враховувати.
Знайти енергію зарядженої кулі радіусом R з провідника в однорідному середовищі з проникливістю . Заряд кулі q.
Знайти енергію рівномірно зарядженої по об’єму діелектричної кулі радіусом R. Діелектрична проникливість кулі , навколишнє середовище – вакуум. Заряд кулі q.
Побудувати картину електростатичного поля коаксіального кабелю, в якого радіус внутрішнього циліндричного провідника r₁=1мм, внутрішній радіус трубчатого провідника r₂=4мм.
Два однакових та протилежних по знаку точкових зарядів +q і –q знаходяться на відстані 2h один від одного. Визначити потенціал та напруженість поля в точці М, яка знаходиться на відстанях r₁ та r₂ від зарядів.
Побудувати картину електростатичного поля диполя.
Два однакових та протилежних по знаку точкових зарядів +q і –q розміщені на кулях з провідника з радіусами R₁ і R₂ відповідно. Відстань між кулями 2h ( , 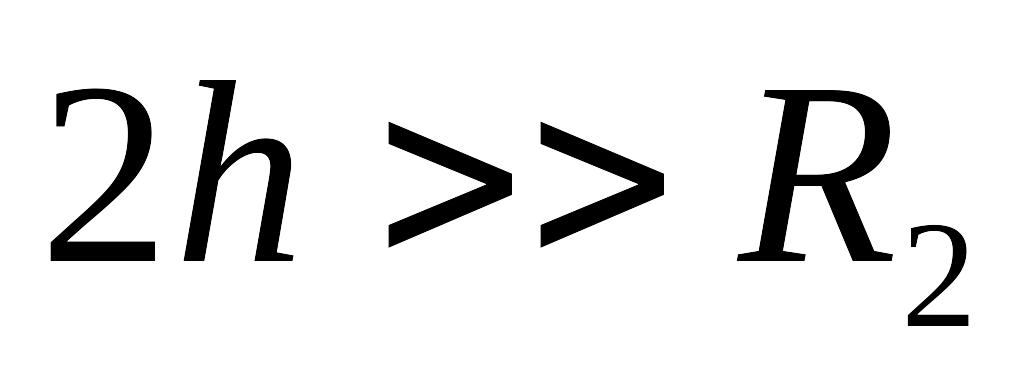). Знайти потенційні коефіцієнти та ємність системи.
Точковий заряд q знаходиться в вакуумі на відстані l від центру заземленої сфери із провідника радіусом R (R<l). Визначити індуційований на сфері заряд, напруженість електростатичного поля біля поверхні сфери та місцезнаходження заряду зображення.
Знайти енергію рівномірно зарядженої по об’єму діелектричної кулі радіусом a та зарядом q. Діелектрична проникливість кулі , навколишнє середовище вакуум.
Знайти енергію зарядженого циліндричного конденсатора з зарядом q довжиною l₀. Радіуси обкладок R₁ та R₂. Між обкладками знаходяться два шари однорідних діелектриків з проникливостями та . Поверхня розподілу між ними – циліндр радіусом R₀. Краєві ефекти не враховувати.
Відстань між обкладками плоского конденсатора d, площа обкладок S. Між обкладками знаходиться діелектрична пластинка. Різниця потенціалів на обкладинках . Яку роботу необхідно виконати, щоб витягти з конденсатора діелектричну пластинку?
Плоский конденсатор у якого відстань між обкладками d, різниця потенціалів на них , вертикально занурили в рідкий діелектрик. На яку висоту підійметься діелектрик між пластинами? Капілярністю знехтувати.
Два конденсатори з ємностями і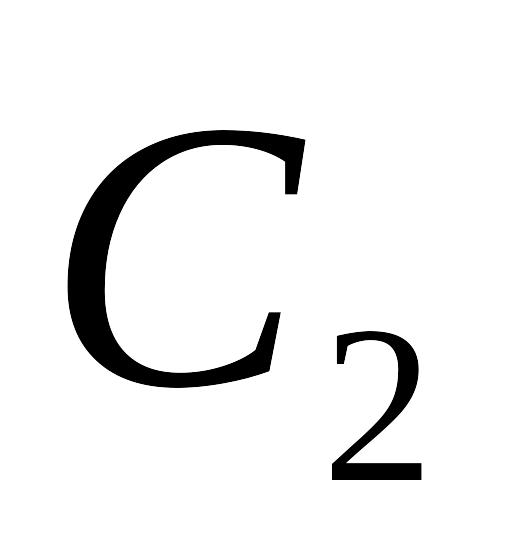 заряджаються до напруги 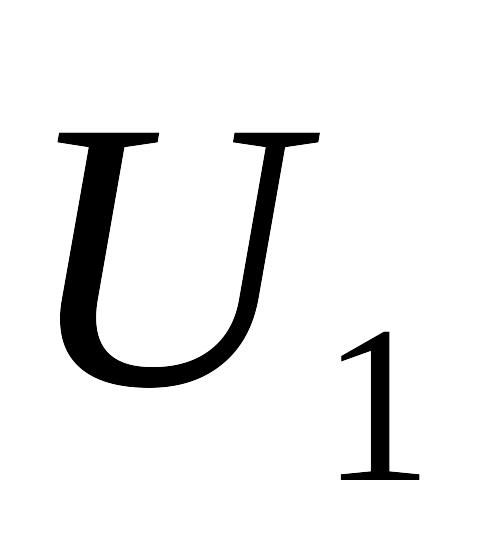і 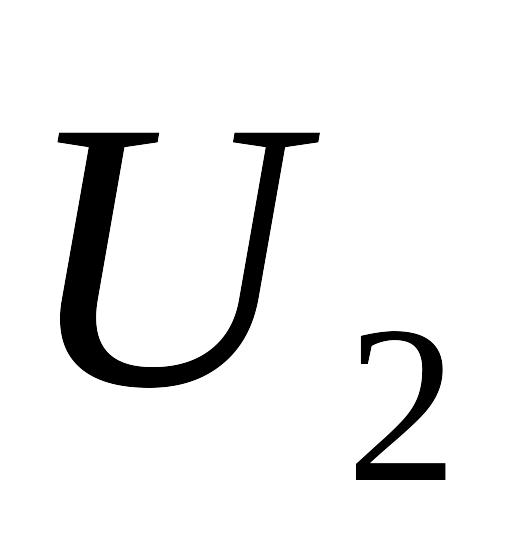. Потім вони з’єднуються між собою. Знайти роботу розряду при а) паралельному; б) послідовному з’єднанні конденсаторів.
Знайти енергію і силу взаємодії двох паралельних нескінченних ниток, рівномірно заряджених з лінійними густинами  та  і розташованих на відстані одна від одної в однорідному середовищі з діелектричною проникливістю .
Визначити силу взаємодії ниток з попередньої задачі за допомогою максвелівського тензора натягу.
Визначити силу взаємодії двох електричних диполів в вакуумі.
Заряджена куля з провідника радіусом і зарядом q розрізана на дві половини. Знайти силу відштовхування між ними в вакуумі.
Точковий заряд q знаходиться в вакуумі на відстані від заземленої площини з провідника. Знайти потенціал, який ним створюється, та напруженість поля.
Два однорідних діелектрика з проникностями і мають спільну границю у вигляді нескінченної площини. В одному діелектрику на відстані від границі знаходиться точковий заряд q. Знайти поле, яке ним створюється.
Визначити поле поблизу кінця тонкого конічного виступу на поверхні провідника.
Знайти взаємну ємність одиниці довжини двох паралельних провідників з радіусами а і b. Відстань між ними R.
Границя провідника являє собою необмежену площину з виступом у вигляді напівсфери. Знайти розподіл зарядів на поверхні.
Знайти поле зарядженого диску радіусом . Виразити його в циліндричних координатах.
Куля рівномірно заряджена по об’єму з густиною ρ. Всередині кулі ексцентрично розташована сферична порожнина. Відстань між центрами кулі та порожнини l. Знайти напруженість електричного поля в порожнині.
Система складається з двох провідників, які віддалені від усіх інших провідників. Провідник 1, розташований всередині порожнистого провідника 2. Виразити ємності конденсатора і провідників, які створюють цю систему через коефіцієнти ємності.
Коефіцієнти ємності системи двох провідників дорівнюють 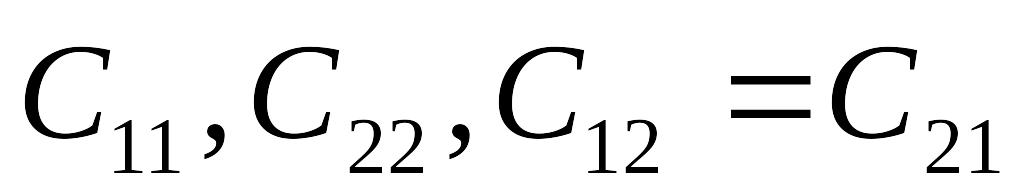. Знайти ємність конденсатора, обкладки якого є ці два провідники.