1.2. Выбор метода решения
Цель данного этапа – определить теоретическую возможность решения и, в таком случае, нахождение формального правила получения решения.
Данный этап плохо формализуется. Это связано с чрезвычайно широким многообразием задач и методов их решения.
Метод решения может быть представлен
в виде системы формул (безусловной или условной)
в виде словесного изложения последовательности действий
в виде их комбинаций.
Описание метода может содержать ограничения на исходные данные, накладываемые методом.
Приведем примеры.
Пример 1. Метод решения задачи «Решение квадратного уравнения» сводится к системе формул:
Применять их можно только при условии, что
Пример 2. Метод решения задачи «Расчет электрической цепи»
Метод можно представить в виде следующей системы формул:
(1)
при
,
а
при
имеет место короткое
замыкание и расчет невозможен.
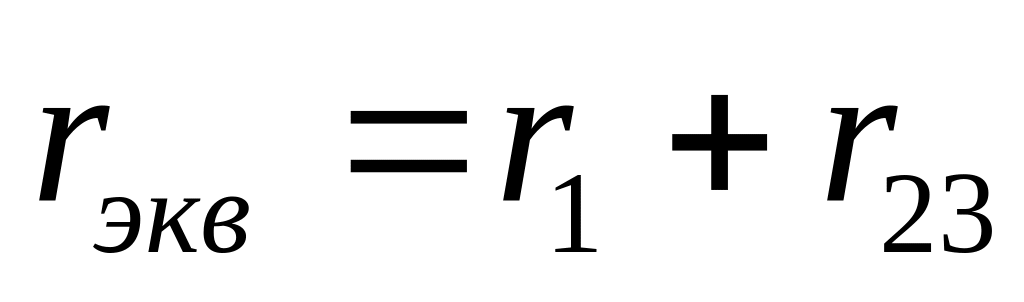
при
при
Примечание. Поскольку это не алгоритм, здесь не обязательно указывать формулы в порядке их вычисления. Важно только, чтобы искомая величина W за счет их применения могла быть вычислена как некая функция от заданных значений напряжения и трех сопротивлений.
Пример 3. Метод решения задачи нахождения наибольшего общего делителя (НОД) двух целых чисел.
В математике известно несколько способов решения этой задачи. Наиболее популярный – разложение исходных чисел на простые сомножители и затем выбор сомножителей, присутствующих в разложении как первого, так и второго чисел.
Реализовать этот метод в виде алгоритма для ЭВМ для начинающих не очень просто. Разработать его самостоятельно будет предложено после получения определенного практического опыта в разработке алгоритмов, а сейчас приведем другой, более простой для понимания и реализации метод – метод Эвклида.
Метод Эвклида позволяет найти НОД двух натуральных чисел и заключается в следующем:
Проиллюстрируем метод на примере.
Пусть заданы числа a=20 и b=34. Тогда:
Шаг |
a |
b |
Действие |
Исходное состояние |
20 |
34 |
|
1 |
20 |
34 |
Уменьшить b на 20 |
2 |
20 |
14 |
Уменьшить a на 14 |
3 |
6 |
14 |
Уменьшить b на 6 |
4 |
6 |
8 |
Уменьшить b на 6 |
5 |
6 |
2 |
Уменьшить a на 2 |
6 |
4 |
2 |
Уменьшить a на 2 |
7 |
2 |
2 |
Остановка: НОД найден |
Обратите внимание, что величина НОД, в принципе, беззнаковая, в связи с чем НОД для чисел (-20, 36) также равен 2. Однако применить описанный метод Эвклида непосредственно нельзя – процесс вычитания меньшего из большего становится бесконечным. Посмотрим, что получится, если применить метод Эвклида для указанных чисел:
Шаг |
a |
b |
действие |
Исходное состояние |
–20 |
34 |
|
1 |
–20 |
34 |
Уменьшить b на –20 |
2 |
–20 |
54 |
Уменьшить b на –20 |
3 |
-20 |
74 |
Уменьшить b на -20 |
4 |
-20 |
94 |
. . . |
Как видно из таблицы, процесс получается бесконечный, и равенства значений a и b не будет никогда. Это связано с тем, что число (–20) является целым, но не натуральным. Однако если взять исходные числа по абсолютной величине, никаких проблем не будет.
Особый случай имеет место, когда хотя бы одно из исходных чисел равно нулю. Ноль входит во множество целых чисел, и поэтому также может быть предъявлен в качестве исходного при программной реализации вычисления НОД. Как видно из алгоритма, НОД в этом случае вычислить невозможно, да в этом и нет необходимости, из-за особого статуса нуля.
С учетом изложенного можно предложить следующий метод решения задачи:
Если оба числа не равны нулю, взять их абсолютные величины и применить алгоритм Эвклида. В противном случае – сообщить об отсутствии решения (Например, выдав сообщение «НОД не определен»).