2.5. Управляющие структуры

Для организации разнообразной последовательности действий в алгоритме используются три вида управляющих структур, обеспечивающих требуемую последовательность. Это – следование, альтернативный выбор и циклическое повторение. При их использовании рекомендуется применять определенные правила записи, которые позволят наглядно представить структуру алгоритма. Такая запись получила название структурной. Далее, при рассмотрении управляющих структур будут излагаться и правила структурной записи.

Рассмотрим их.

Следование. Данное правило определяет следующее: два действия (в частности, например, две операции) связаны отношением следования в том случае, если второе действие выполняется после окончания первого, начинает выполняться в момент завершения первого и выполняется вне зависимости от результата первого действия.

При структурной записи следования двух действий в алгоритме их тексты должны располагаться друг под другом, и начинаться они должны с одинаковым отступом от края листа. Если для записи некоторого действия требуется более одной строки, все строки кроме первой должны записываться с отступом вправо по отношению к первой строке. Это позволит сделать более наглядной структуру алгоритма.

Н иже приведены графическое и текстовое изображение двух действий, связанных отношением следования.

Два действия, связанные отношением следования, при изображении алгоритма можно рассматривать как одно, имеющее одну точку входа и одну точку выхода.

Конкретные примеры использования как данной, так и других структур будут приведены ниже.

Альтернативный выбор. Данная конструкция применяется в случае, когда в процессе выполнения алгоритма дальнейшие действия связываются с выполнением некоторого условия. Различают следующие варианты данной конструкции: одноальтернативная (а), двухальтернативная (б) и многоальтернативная (в).

При записи данной конструкции используются специально зарезервированные (ключевые) слова – если, то, инес (от слов иначе-если), иначе и все. Для того чтобы в тексте алгоритма эти слова выделялись, они будут изображаться подчеркнутыми. Ниже приведены типовые формы их записи.

(а)

В

если <условие> то

действие-1

все

ариант (а) изображает конструкцию, в которой действие-1 выполняется, если истинно условие. В противном случае ничего не выполняется, но в любом случае после этого выполняется действие, следующее за данной конструкцией.

(б)

если <условие> то

действие-1

иначе

действие-2

все

Вариант (б) используется, когда действие-1 выполняется при истинности условия, а во всех остальных случаях выполняется действие-2.

(в)

В

если <условие1> то

действие-1

инес <условие2> то

действие-2

иначе

действие-3

все

ариант (в) представляет наиболее общий случай. Он изображает ситуацию, когда выполнение любого действия, кроме последнего, связано с истинностью (выполнением) соответствующего условия. Из этой конструкции можно построить структуру с произвольным числом альтернатив. Для этого достаточно повторить элемент инес требуемое число раз: 0, 1, 2, …, а элемент иначе, при необходимости, можно опустить.

Любой вариант конструкции “альтернативный выбор” имеет одну точку входа (слово если) и одну точку выхода (слово все). И в этом смысле она может быть связана отношением следования с любым другим действием алгоритма. Точно так же любая из альтернатив может рассматриваться не как единое действие, а как несколько действий, связанных отношением следования.

Циклическое повторение. Данная конструкция предназначена для задания многократного повторения одного и того же действия (или группы действий). В программировании эту конструкцию называют просто конструкцией цикл, а повторяющиеся действия – телом цикла.

Можно выделить три основных варианта данной конструкции: “цикл с предусловием”, “цикл с постусловием” и “цикл со счетчиком”. Рассмотрим их.

(

цикл-пока <условие>

тело-цикла

кцикл

а) Цикл с предусловием записывается следующим образом:

Принцип выполнения конструкции:

Вначале проверяется условие, записанное после ключевого слова цикл-пока, и если оно истинно, выполняется тело цикла. После достижения ключевого слова кцикл (аббревиатура от слов “конец цикла”) происходит возврат на повторную проверку условия, записанного в начале конструкции. В случае нарушения истинности условия выполнение конструкции завершается и происходит переход к действию алгоритма, следующему за циклом.

Из изложенного следует, что тело цикла может быть не выполнено ни разу, если в первый момент условие не выполняется, и может повторяться неопределенное число раз. Если условие выполняется всегда, выхода из данной конструкции может не произойти никогда. Такая ситуация называется зацикливанием, и разработчик алгоритма должен сам позаботиться о том, чтобы избежать ее. Очевидно, что для ограничения числа повторений в теле цикла должны происходить изменения переменных, которые используются в условии.

Пример конструкции “цикл с предусловием” (ее иногда называют “цикл-пока”) во фрагменте алгоритма:

Здесь тело цикла составляют две операции присваивания, связанные отношением следования. Их выполнение повторяется до тех пор, пока истинно условие “S<35”, а поскольку значение переменной S монотонно возрастает, то в некоторый момент условие перестанет выполняться и, соответственно, прекратится выполнение всей конструкции.

(б) Цикл с постусловием записывается следующим образом:

Принцип выполнения:

Вначале выполняется тело цикла, затем проверяется условие, записанное после ключевого слова кцикл-до. Если условие не выполняется (ложно), происходит возврат на начало, и тело цикла выполняется вновь. Этот процесс повторяется до тех пор, пока при очередной проверке условие не примет истинного значения, и в этом случае выполнение конструкции завершается и происходит переход к действию алгоритма, следующему за циклом. Здесь также возможно зацикливание.

Описываемая конструкция, как и предыдущая, является конструкцией с неопределенным числом повторений тела цикла. Основное отличие этой конструкции от предыдущей заключается в том, что в ней тело цикла выполняется хотя бы один раз.

Пример конструкции “цикл с постусловием” (ее иногда называют “цикл-до”) во фрагменте алгоритма:

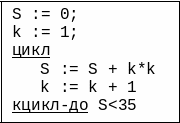
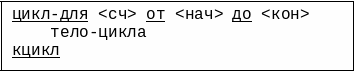
(в) Цикл со счетчиком записывается следующим образом:

Здесь

сч - имя скалярной переменной целого типа, выполняющей функции счетчика числа повторений тела цикла (ее называют счетчиком или параметром цикла)

нач - целочисленное выражение, которое задает начальное значение счетчика цикла

кон - целочисленное выражение, которое задает конечное значение счетчика цикла.

Полагается, что с каждым повторением тела цикла значение счетчика изменяется (увеличивается или уменьшается ) на единицу. Отсюда, данная конструкция такова, что число повторений тела цикла в ней всегда конечно и его можно точно вычислить. Поэтому ее называют конструкцией цикла с определенным числом повторений.

Принцип выполнения: Изложим его для случая, когда с каждым повторением тела цикла значение счетчика увеличивается на 1. Вначале счетчику цикла присваивается начальное значение. Затем производится проверка, не превысило ли текущее значение счетчика конечной величины. Если это условие истинно, выполняется тело цикла. После этого значение счетчика увеличивается на 1, и производится возврат в начало цикла, где вновь проверяется, как соотносятся между собой текущее значение счетчика цикла и конечного значения. Процесс повторений прекращается и происходит переход к действию, записанному после рассматриваемой конструкции цикла, когда текущее значение счетчика превысит конечное значение.

Анализ описанной логики исполнения показывает, что, во-первых, тело цикла может быть не выполнено ни разу, и, во-вторых, что здесь невозможно зацикливание.

Имеется одно существенное замечание: счетчик цикла можно использовать, но нельзя изменять в теле цикла.

Пример конструкции “цикл со счетчиком” во фрагменте алгоритма:

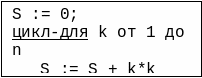
Здесь k – счетчик цикла, и он принимает последовательно значения: 1, 2, . . ., n. За счет этого, после завершения цикла, переменная S примет значение суммы квадратов указанных выше значений счетчика цикла: .