2.22 Импульсные системы

Импульсными называют системы, в которых хотя бы одна из величин, характеризующих состояния системы, квантуется по времени.

Импульсные САУ содержат в своем составе один или несколько импульсных элементов (ИЭ) и непрерывную часть (НЧ). Функциональная схема импульсной системы может иметь, например, вид, представленный на рис. 2.22.1.

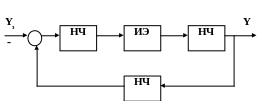
Рис. 2.22.1 Пример функциональной схемы импульсной системы

Преобразование непрерывного сигнала в импульсный называется импульсной модуляцией.

Существуют три вида импульсной модуляции: амплитудно-импульсная модуляция (АИМ), широтно-импульсная модуляция (ШИМ) и время-импульсная модуляция (ВИМ). Время-импульсная модуляция, в свою очередь, подразделяется на фазоимпульсную модуляцию (ФИМ) и частотно-импульсную модуляцию (ЧИМ).

При амплитудно-импульсной модуляции амплитуда (высота) А импульсов изменяется в зависимости от изменения входного непрерывного сигнала Х, период Т следования импульсов и их длительность t остаются неизменными (рис. 2.22.2).

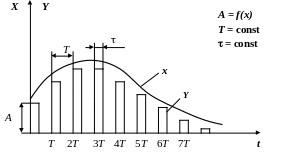
Рис. 2.22.2 Амплитудно-импульсная модуляция:

Х  входной непрерывный сигнал; Y  выходной импульсный сигнал

При широтно-импульсной модуляции длительность t следования импульсов изменяется в зависимости от изменения входного непрерывного сигнала Х, период Т следования импульсов и их амплитуда (высота) А остаются неизменными (рис. 2.22.3).

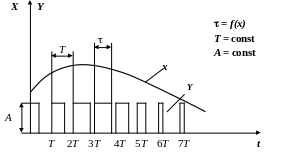
Рис. 2.22.3 Широтно-импульсная модуляция:

Х  входной непрерывный сигнал; Y  выходной импульсный сигнал

При фазоимпульсной модуляции сдвиг по времени (по фазе) a импульсов относительно моментов времени квантования 0, Т, 2Т, 3Т… изменяется в зависимости от изменения входного непрерывного сигнала Х, период Т следования импульсов, их длительность t и амплитуда (высота) А остаются неизменными (рис. 2.22.4).

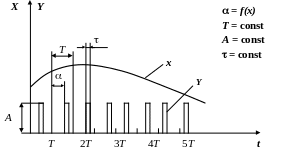
Рис. 2.22.4 Фазоимпульсная модуляция:

Х  входной непрерывный сигнал; Y  выходной импульсный сигнал

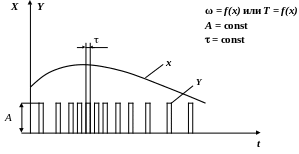При частотно-импульсной модуляции частота следования w (период Т) импульсов изменяется в зависимости от изменения входного непрерывного сигнала Х, длительность импульсов t и их амплитуда (высота) А остаются неизменными (рис. 2.22.5).

Рис. 2.22.5 Частотно-импульсная модуляция:

Х  входной непрерывный сигнал; Y  выходной импульсный сигнал

В системы автоматического управления и регулирования импульсные элементы вводятся для повышения надежности, точности, помехозащищенности, упрощения систем, управления скоростью исполнительных механизмов постоянной скорости путем импульсного прерывания сигнала, управляющего движением исполнительного механизма, и т.д.

Импульсные элементы легко сопрягаются с цифровыми устройствами. Кроме того, импульсные элементы вводятся в системы автоматического регулирования с объектами управления, обладающими большим транспортным запаздыванием для прерывания изменения управляющего воздействия на объект, что существенно улучшает динамические качества таких систем.

Подробно с математическим описанием и методами исследования импульсных систем можно познакомиться в литературе по автоматическому управлению и регулирования, например [6, 7]. Универсальным методом исследования является моделирование на ЭВМ.