2.16 Устойчивость систем. Условия и критерии устойчивости линейных систем
Устойчивость это свойство системы возвращаться в исходный или близкий к нему установившийся режим после снятия воздействия, вызвавшего выход из установившегося режима.
Выходная величина устойчивой системы остается ограниченной в условиях действия на систему ограниченных по величине воздействий.
Неустойчивая система является неработоспособной, поэтому проверка устойчивости является обязательным этапом анализа системы, а обеспечение устойчивости обязательным условием синтеза.
В общем случае качество нелинейных систем зависит от величины воздействий. Системы устойчивые при одних воздействиях могут быть неустойчивы при других воздействиях. В связи с этим существуют понятия устойчивости в малом, в большом и в целом (абсолютная устойчивость).
Устойчивость в малом устойчивость при бесконечно малых отклонениях от исходного режима.
Устойчивость в большом устойчивость при конечных отклонениях от исходного режима, возможных в данной системе по условиям работы.
Устойчивость в целом устойчивость при неограниченных отклонениях.
В линейных системах таких градаций устойчивости не существует. Линейная система либо неустойчива, либо находится на границе устойчивости, либо устойчива в целом. При этом будут устойчивы не только положения равновесия системы, но и любые вынужденные процессы.
Движение системы имеет две составляющие:
, (2.16.1)
где
свободная составляющая
движения, когда воздействия на систему
отсутствуют;Yвын
вынужденная
составляющая установившегося движения
системы при наличии воздействия.
Из определения устойчивости, следует, что у устойчивых систем свободная составляющая затухает.
Ниже приведены примеры реакции устойчивых и неустойчивых систем на импульсное и ступенчатое воздействия.
t
а)
t
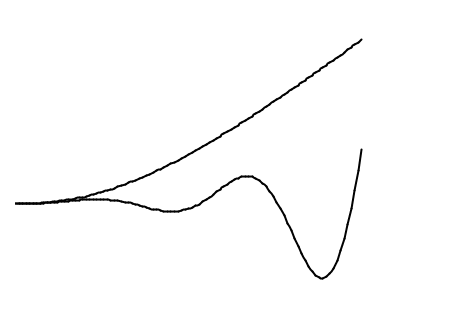
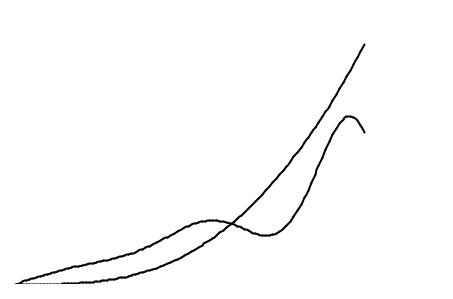
б)
Рис. 2.16.1 Примеры реакций неустойчивых систем на импульсное (а)
и ступенчатое (б) воздействия
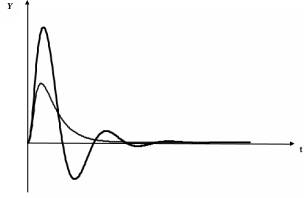
а
t
t
б)
Рис. 2.16.2 Примеры реакций устойчивых систем на импульсное (а)
и ступенчатое (б) воздействия