5. Импульсная переходная функция звена:

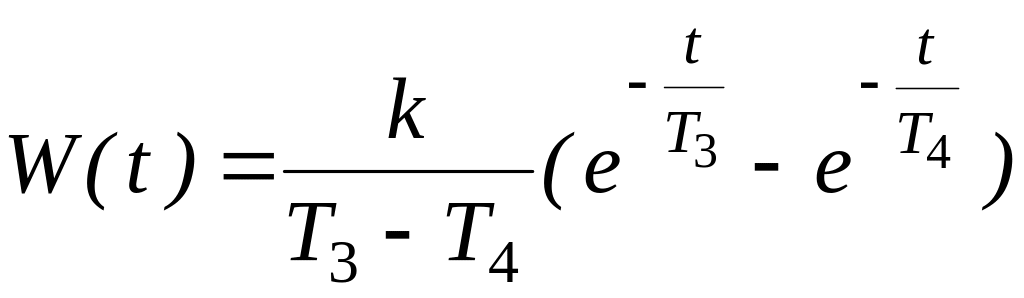. (2.10.26)

W(t)

t

0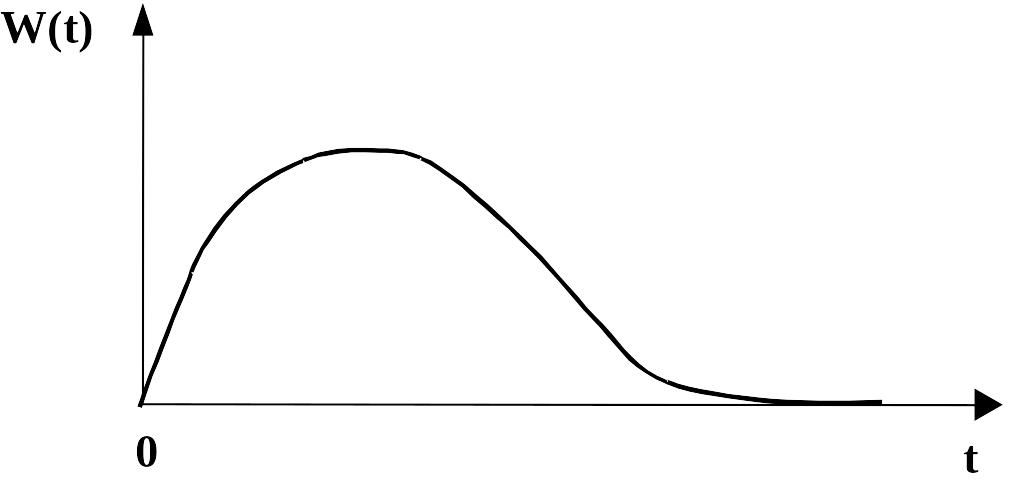

Рис. 2.10.13 Импульсная переходная функция апериодического звена 2-го порядка

6. Частотные характеристики звена:

; (2.10.27)

; (2.10.28)

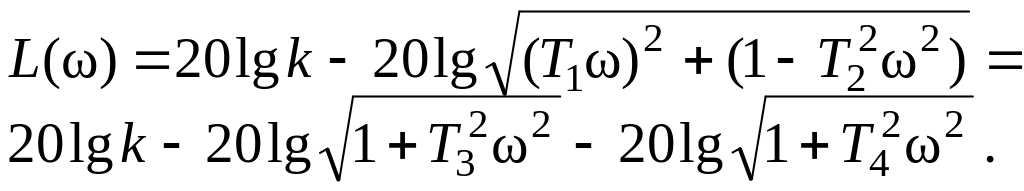(2.10.29)

()

наклон – 20 дБ/дек

наклон – 40 дБ/дек

L()

20lgk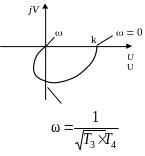

lg

_с1=1/T₃ _с2=1/T₄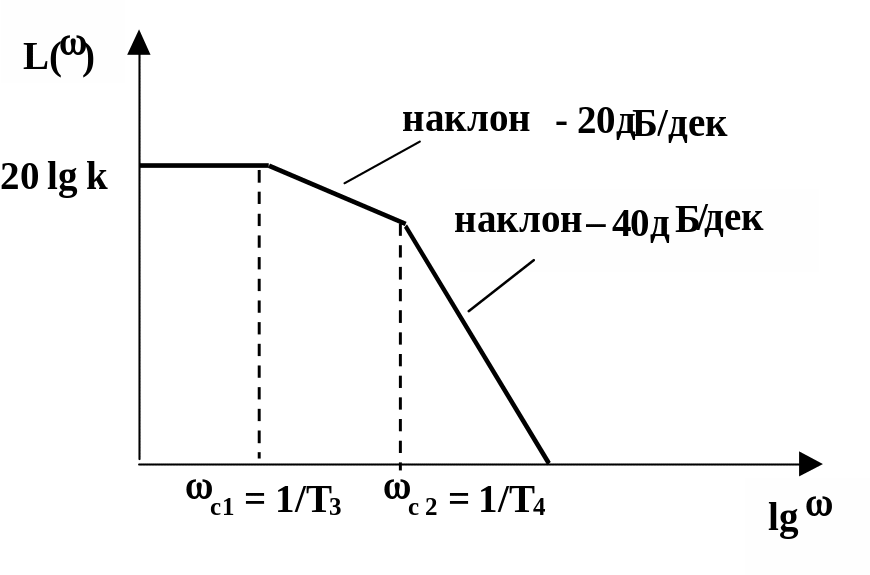

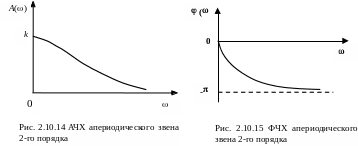
Рис. 2.10.16 АФЧХ апериодического Рис. 2.10.17 ЛАХ апериодического

звена 2-го порядка звена 2-го порядка (сплошной линией

показана асимптотическая ЛАХ)

Колебательное звено

1.Уравнение звена:

. (2.10.30)

Постоянные времени T₁ 2T₂, или .

2. Статическая характеристика звена: Y = kx . (2.10.31)

3. Передаточная и частотная передаточная функции звена:

; (2.10.32)

(2.10.33)

4. Переходная функция звена:

_, (2.10.34)

г

k

Y₁

Y₂

h(t)



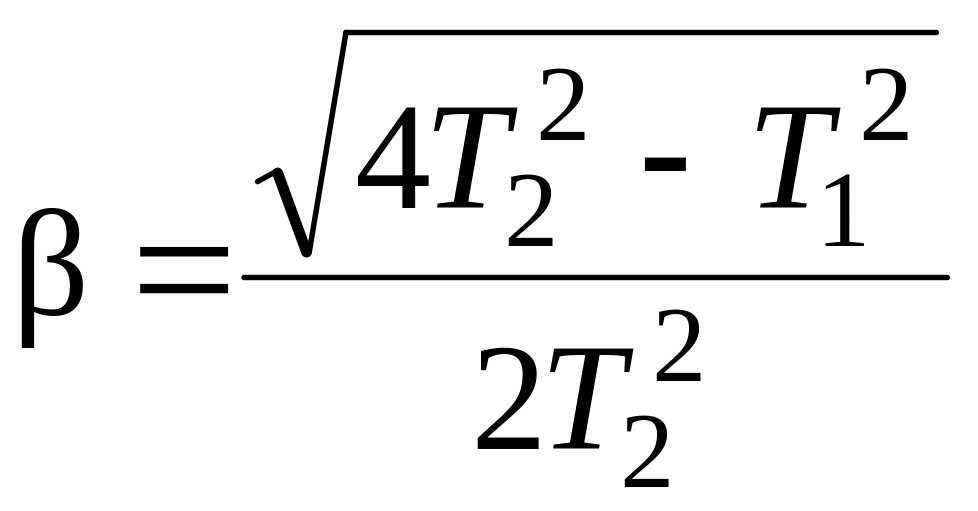де ,  действительная и мнимая части корней характеристического уравнения звена.

t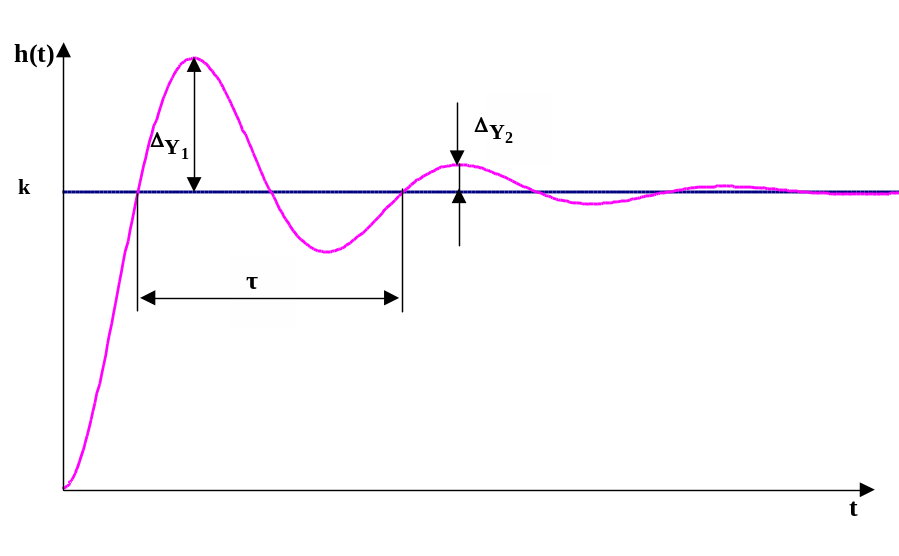

Рис. 2.10.18 Переходная функция колебательного звена

Величина  является частотой колебаний и может быть определена из графика переходной функции:

=2/. (2.10.35)

Величина  характеризует степень затухания колебаний и может быть найдена из графика переходной функции:

; (2.10.36)

. (2.10.37)

5. Импульсная переходная функция звена:

. (2.10.38)

6. Частотные характеристики звена:

; (2.10.39)

(2.10.40)

. (2.10.41)

W(t)

t

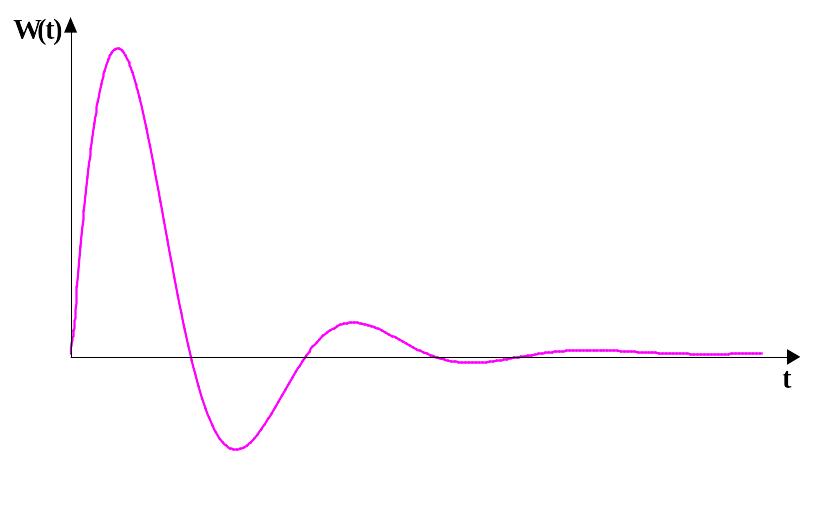
Рис. 2.10.19 Импульсная переходная функция колебательного звена

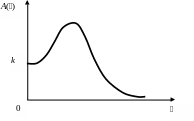
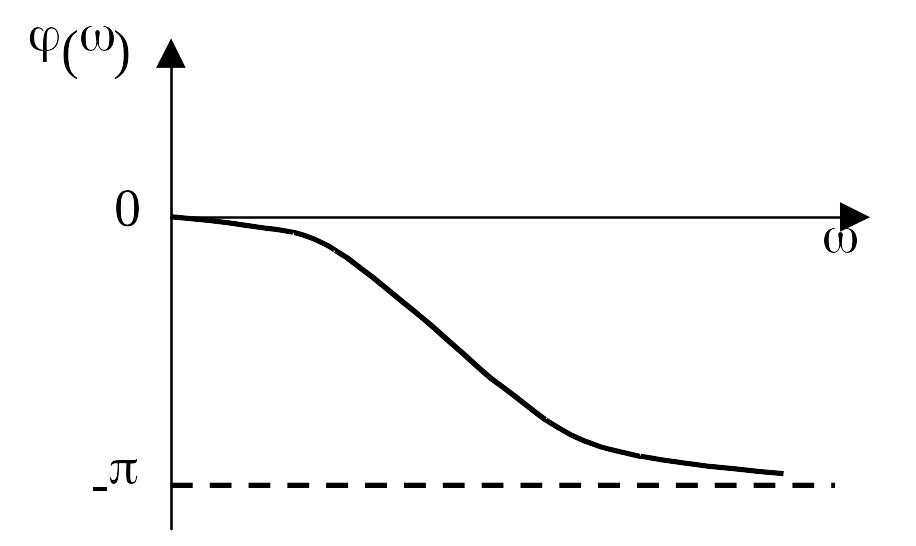
Рис. 2.10.20 АЧХ колебательного звена Рис. 2.10.21 ФЧХ колебательного звена

jV

k

L()

20lgk

наклон – 40 д Б/дек

U

lg

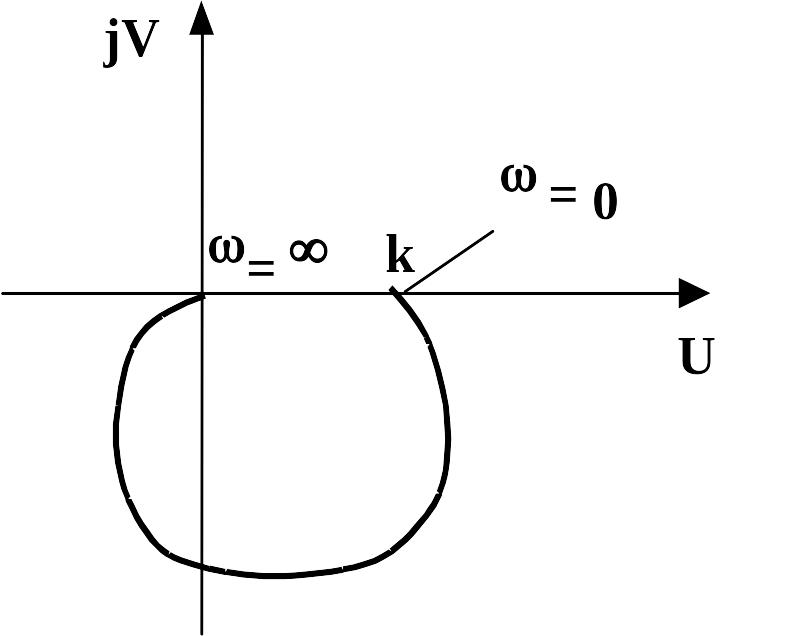
Рис. 2.10.22 АФЧХ колебательного звена

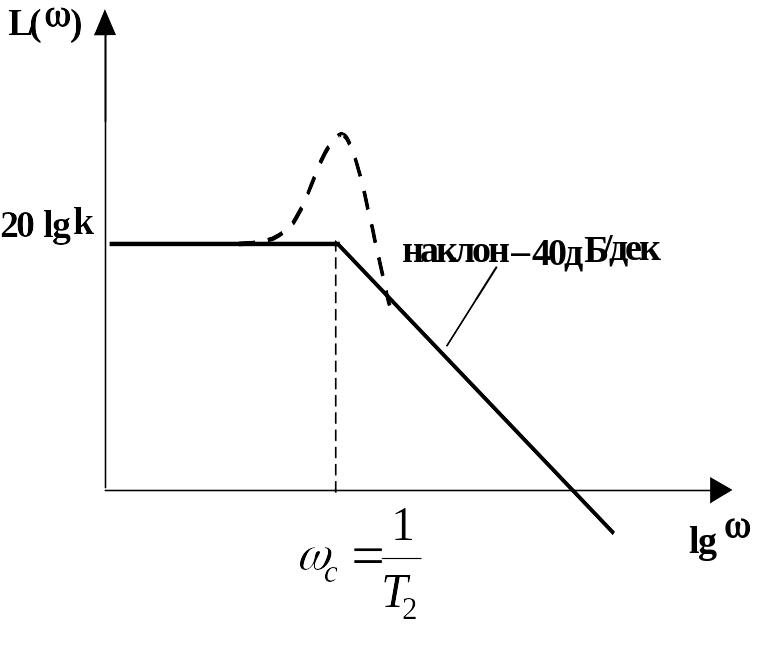
Рис. 2.10.23 ЛАХ колебательного звена (сплошной линией показана асимптотическая ЛАХ)

В окрестностях частоты _с асимптотическая ЛАХ существенно отличается от действительной ЛАХ, поэтому в учебниках и справочниках имеются графики поправок к асимптотической ЛАХ.

Интегрирующее звено

1.Уравнение звена:

, или . (2.10.42)

2. Статическая характеристика звена.

У звена нет статической характеристики, поскольку при постоянном входном воздействии х выходная величина Y постоянно нарастает: . Это звено относится к астатическим звеньям.

Примечание.

Ранее рассмотренные звенья относятся к статическим звеньям.

3. Передаточная и частотная передаточная функции звена:

; (2.10.43)

. (2.10.44)

4. Переходная функция звена:

h(t) = kt. (2.10.45)

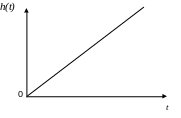
Рис. 2.10.24 Переходная функция Рис. 2.10.25 Импульсная переходная

интегрирующего звена функция интегрирующего звена

5. Импульсная переходная функция звена:

. (2.10.46)

6. Частотные характеристики звена:

(2.10.47)

; (2.10.48)

. (2.10.49)

A()

0



Р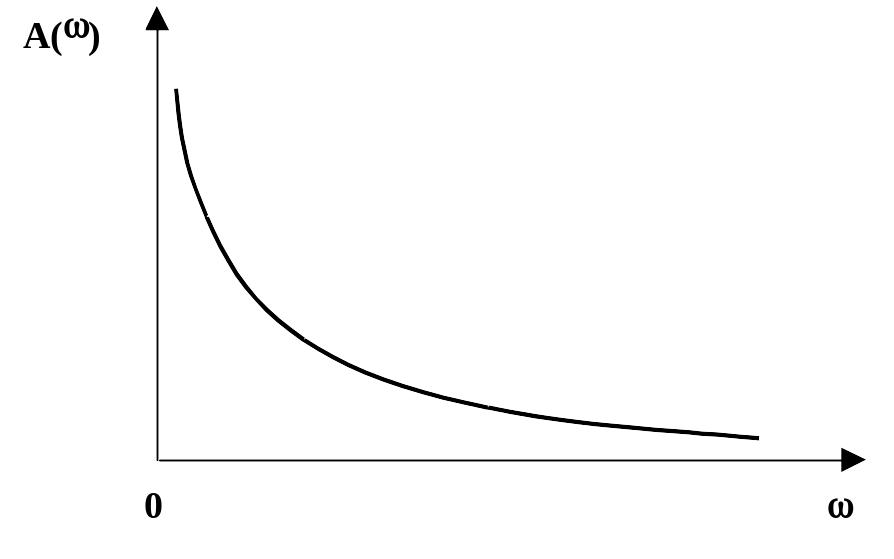 ис. 2.10.26 АЧХ интегрирующего звена

jV

U

 = 

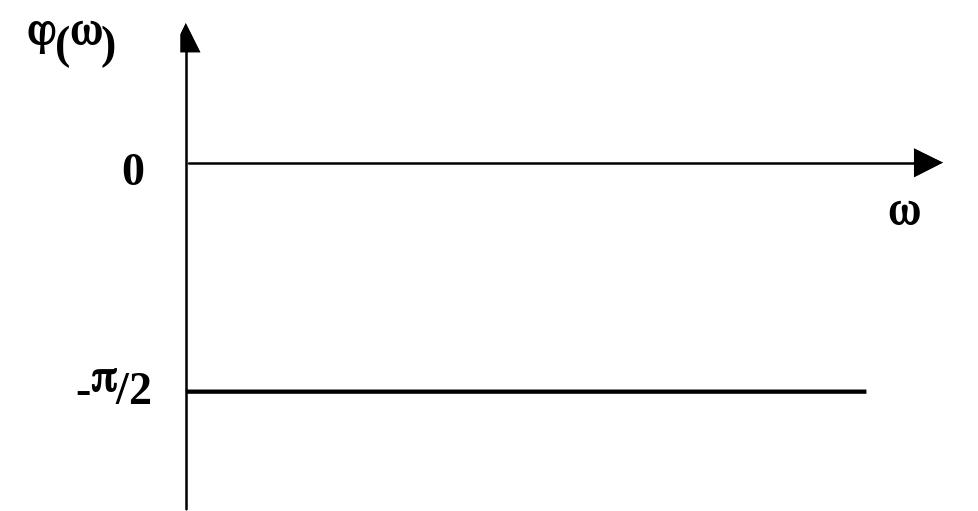
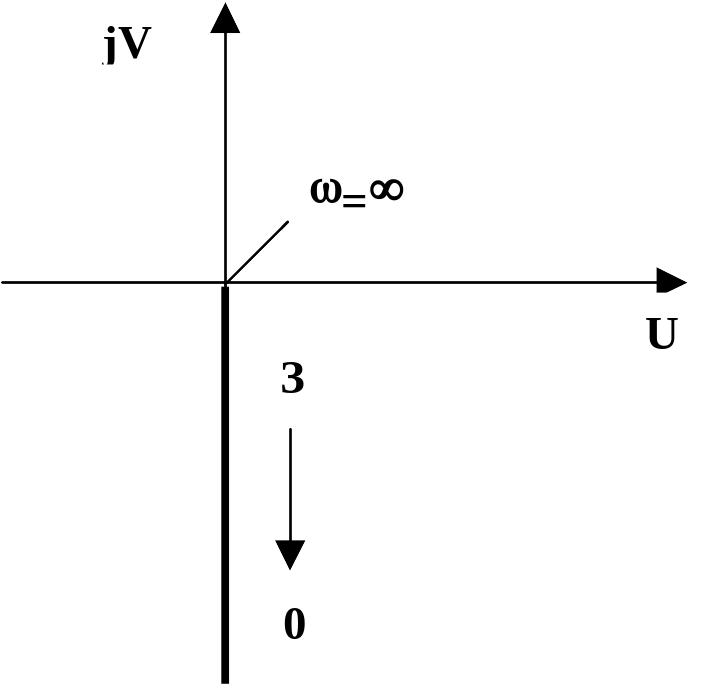
Рис. 2.10.27 ФЧХ интегрирующего звена Рис. 2.10.28 АФЧХ интегрирующего звена

L()

_c = k

наклон-20 дБ/дек

lg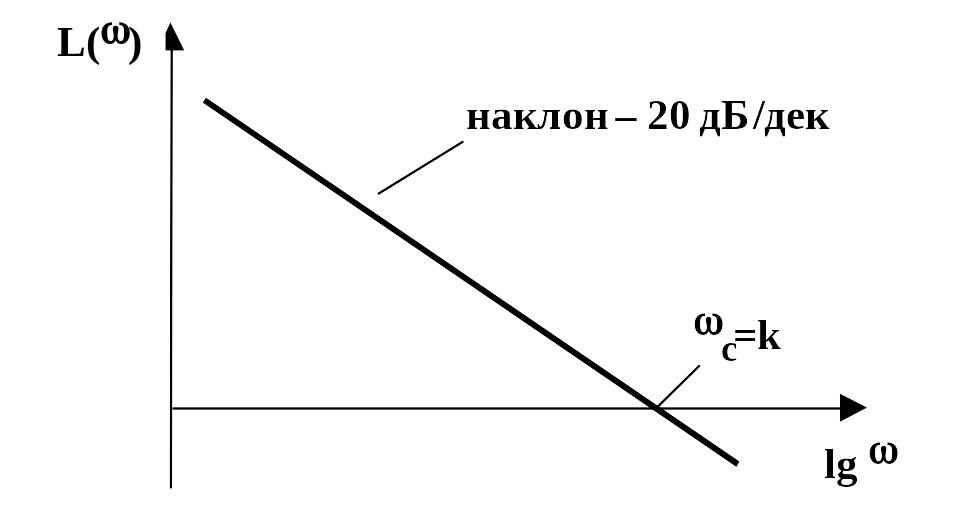

Рис. 2.10.29 ЛАХ интегрирующего звена

Дифференцирующее звено

1. Уравнение звена: . (2.10.50)

2. Статическая характеристика звена: Y=0. (2.10.51)

3. Передаточная и частотная передаточная функции звена:

; (2.10.52)

. (2.10.53)

4

h(t)

. Переходная функция звена: . (2.10.54)

t

0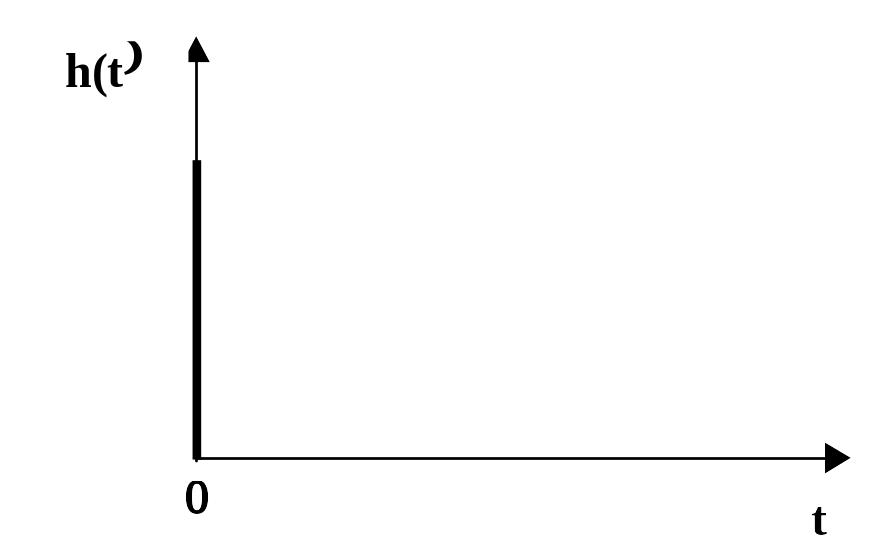

Рис. 2.10.30 Переходная функция дифференцирующего звена

5. Импульсная переходная функция звена:

. (2.10.55)

W(t)

t

0

Рис. 2.10.31 Импульсная переходная функция дифференциального звена

6. Частотные характеристики звена:

(2.10.56)

; (2.10.57)

. (2.10.58)

A()



0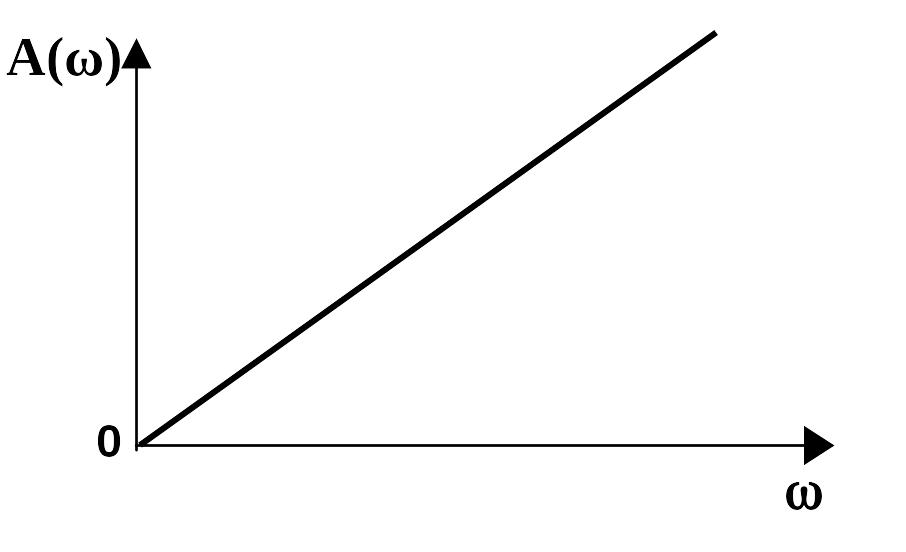

Рис. 2.10.32 АЧХ дифференцирующего звена

/2

Рис. 2.10.33 ФЧХ дифференцирующего звена

jV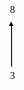

 = 0

U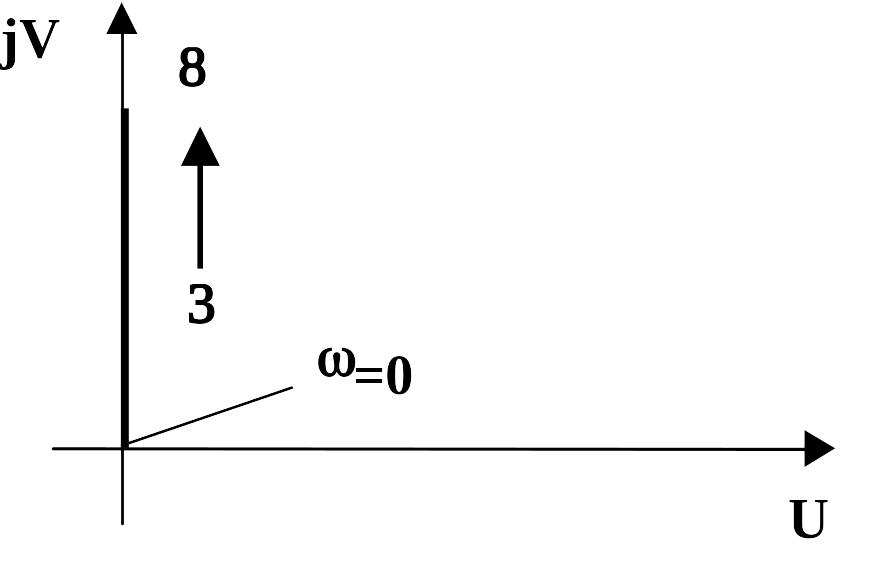

Рис. 2.10.34 АФЧХ дифференцирующего звена

L()

_c = 1/k

lg

наклон + 20 дБ/дек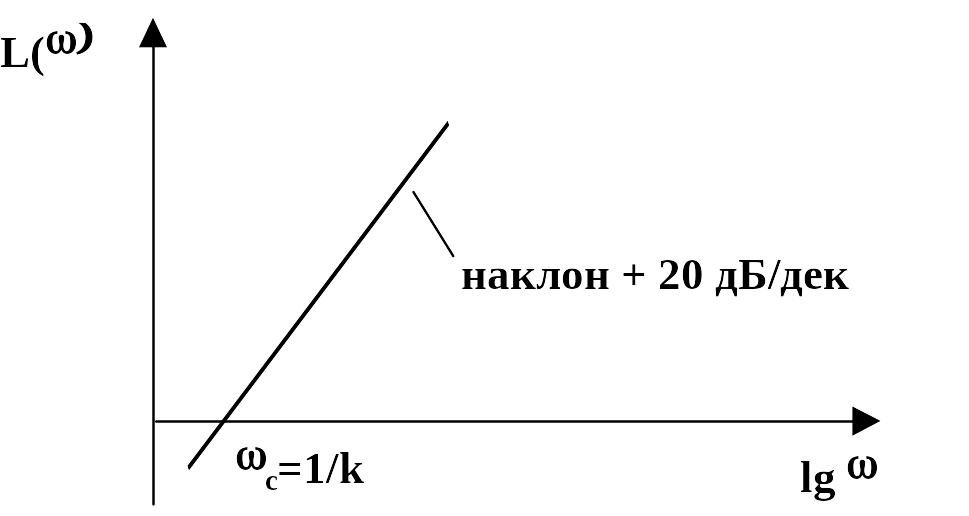

Рис. 2.10.35 ЛАХ дифференцирующего звена