Контрольные вопросы

1. Направления технической подготовки производства.

2. Основные этапы научно-исследовательских работ и их содержание.

3. Понятия «патент» и «лицензия».

4. Этапы конструкторской подготовки производства.

5. Задачи технологической подготовки производства.

6. Назначение пилотной установки.

7. Содержание технологического регламента.

8. Содержание материальной подготовки.

9. Какую роль выполняют ЕСКД и ЕСТД в ходе подготовки производства.

10. Задачи организационной подготовки производства.

11. Методы перехода на выпуск новой продукции и их характеристика.

12. Методы планирования работ по подготовке производства.

13. Элементы сетевого графика и их характеристика.

14. Что показывает критический путь на сетевом графике.

15. Цель оптимизации сетевого графика.

Практическое занятие №3

ТЕХНИЧЕСКАЯ ПОДГОТОВКА ПРОИЗВОДСТВА

Цель занятия: 1. Овладение методикой построения и расчета сетевой модели.

2. Приобретение навыков по экономическому обоснованию организационно-технических мероприятий.

Вопросы для обсуждения

1. Основные задачи комплексной технической подготовки производства

2. Пути ускорения конструкторской подготовки производства

3. Пути ускорения технологической подготовки производства

4. Какие факторы влияют на организацию работ по подготовке производства

5. Преимущества системы СПУ

6. Что отражает сетевой график?

7. Управление комплексом работ с помощью СПУ.

Методические указания для решения задач

1) Сетевое планирование и управление

Правила построения сетевого графика.

При построении графиков разные работы не должны обозначатся одной и той же цифрой. В сети не должно быть тупиковых событий, от которых не начинается ни одна работа, “хвостовых” событий, когда событию не предшествует ни одна работа, за исключением исходного события, “замкнутых” контуров, т.е. путей, которые соединяют начальное событие с ним же самими.

При построении сетевого графика необходимо придерживаться ряда правил и рекомендаций:

• каждая работа должна иметь начальное и конечное событие;

• ни одна работа не может начинаться, пока не наступило событие, предшествующее ей, ни одно событие не может считаться завершенным, пока не закончены все работы, ведущие к нему;

• если к одному событию подходит несколько работ разной продолжительности, то целесообразно вводить дополнительную фиктивную работу;

• ни одна работа и ни один путь не могут дважды проходить через одно событие.

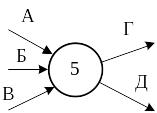
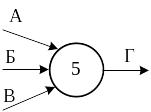
Рассмотрим некоторые правила построения сетевых графиков (рис. 3.2).

а)

б) в) г)

д) е)

Рис. 3.2. Сочетание событий и работ на сетевом графике

При выполнении следующих друг за другом работ каждая последующая работа может быть начата только после выявления результатов предшествующих работ, т. е. после свершения определенного события. На сети это изображается так, как показано на рис. 3.2а. На рис. 3.2б, 3.2в, 3.2г, 3.2д, 3.2е изображены различные варианты сочетания событий и работ.

График строят без учета временной шкалы, но на его основе определяют конкретные сроки проведения работ. Зная продолжительность выполнения каждой работы, суммированием легко определить продолжительность выполнения каждой последовательности работ.

Расчет сетевого графика

После вычисления продолжительности работ по формулам (3.9, 3.10) рассчитываются остальные параметры сетевой модели:

- ранний и поздний срок событий i;

- ранние сроки начала и окончания работ (i,j);

- поздние сроки начала и окончания работ (i,j);

R(i) – резерв времени события i;

R(z) – резерв времени пути z;

- полный резерв времени работы (i,j).

Расчет указанных параметров студентов должен уметь осуществить любым из рассмотренных ниже методов расчета сети.

Аналитический метод расчета

1. Определение ранних сроков

Ранний срок свершения события – срок, необходимый для выполнения всех работ, предшествующих данному событию; определяется продолжительностью максимального из путей, ведущих от исходного события к данному:

(3.24)

Ранний срок начала работы характеризуется ранним сроком свершения начального для данной работы события i:

(3.25)

Ранний срок окончания работ :

(3.26)

2. Определение поздних сроков

Поздний срок свершения события – срок, превышение которого вызовет соответствующую задержку свершения завершающего события:

(3.27)

Последний срок окончания работы:

(3.28)

Последний срок начала работы

(3.29)

3. Определение резервов времени

Резерв времени события:

(3.30)

Резерв времени пути показывает предельно допустимое увеличение этого пути:

(3.31)

Полный резерв времени работы показывает предельно допустимое увеличение продолжительности этой работы:

(3.32)

или

(3.33)

Свободный резерв времени работы:

(3.34)

Графический метод расчета сетевой модели

Графический метод предполагает расчет модели по событиям: непосредственно на графике определяется ранний срок , поздний срок и резерв времени события . Для расчета по этой методике каждое событие разбивается на 4 сектора (рис. 3.3): в верхний сектор заносится номер события, а левый – ранний срок свершения события, в правый – поздний срок свершения события, в нижний – резерв времени события.

Рис.3.3. Расчет модели по событиям

При определении ранних сроков свершения событий расчет ведется последовательно от начального события к конечному, при определении же поздних сроков порядок обратный – от конечного события к начальному.

Расчет сетевого графика с помощью теории графов

Для расчета сети на основе этого метода следует заполнить матрицу связей между событиями. Матрица связей представляет собой шахматную таблицу с числом столбов (j) и строк (i), равным количеству событий в сетевом графике, на пересечении i-ой строки и j-ого столбца проставляется продолжительность работы (i,j).

Указанный метод позволяет определить

Ранний срок определяется величиной максимального пути, ведущей от начального события к данному, т.е. максимальный из парных сумм, где первое слагаемое - предшествующего события, а второе – продолжительность работы, соединяющей данное событие с предыдущим.

Поздний срок определяется как минимальная из парных разностей, где уменьшаемое является последующего события, а вычитаемым – продолжительность работы, соединяющей данное -е событие с последующим.

Резервы событий определяют непосредственно в таблице как разницу позднего и раннего сроков свершения событий.

Критический путь определяется величиной раннего или позднего срока свершения конечного события.

Все эти параметры следует научиться рассчитывать, не прибегая к графику, а пользуясь только его матричной формой записи.