1. Линейчатые поверхности.

Линейчатая поверхность в общем случае однозначно определяется тремя направляющими линиями. Действительно, пусть даны три пространственные кривые линии , и (рис. 1). Возьмем на кривой произвольную точку М, примем ее за вершину конической поверхности , а за направляющую этой поверхности примем дугу кривой . Если N – точка пересечения дуги кривой с поверхностью , то (MN) пересечет дугу кривой в точке L. То , что (MN) обязательно пересечет дугу кривой , не вызывает сомнения, так как (MN) и кривая принадлежат одной и той же плоскости . Из рис. 1 видно, что через точку М, взятую на направляющей , проходит прямолинейная образующая g, пересекающая две другие направляющие и . Задавая другое положение точки М  М₁, и принимая точку M₁ за верши­ну конической поверхности, мы получим при той же направляющей отсек новой конической поверхности ₁, которую дуга кривой пересе­чет в точке N₁. Точки M₁ и N₁ определяют прямую (M₁ N₁) , которая пе­ресечет третью направляющую в точке L₁. (M₁ L₁) — новая обра­зующая g₁ линейчатой поверхности.

Описанным способом можно построить любое число прямолиней­ных образующих, которые выделят в пространстве одну единственную линейчатую поверхность. Следует иметь в виду, что нельзя за направ­ляющие брать три различные по форме и произвольно расположен­ные линии. Произвольно можно задавать только две направляющие, форму и положение третьей направляющей выбирают так, чтобы она находилась внутри конгруенции прямых, определяемой двумя уже взятыми направляющими.

Чтобы третья направляющая принадлежала линейчатой поверхности, она должна входить внутрь конгруенции, определяемой первыми двумя направляющими. Иными словами, задав дуги двух направляющих линейчатой поверхности, мы определяем область ее существования. На рис.2 эта область ограничена линиями красного цвета. Очевидно, дуга кривой , ограниченная точками L и L_n , будет принимать участие совместно с дугами кривых () и (NN_n) в образовании линейчатой поверх­ности (LL_n лежит внутри конгруенции). Кривая может быть исполь­зована в качестве третьей направляющей только на участке FF_n (т.е. в той части, которая лежит внутри конгруенции).

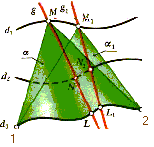
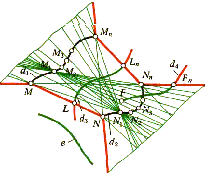
Рис. 1 Рис. 2

Кривая е, не погруженная в область конгруенции прямых, не бу­дет принадлежать линейчатой поверхности и, следовательно, не мо­жет быть принята за третью направляющую.

Теперь, после того как мы познакомились с требованием к зада­нию третьей направляющей линейчатой поверхности, можно перейти к рассмотрению различных групп этих поверхностей и, в частности, рассмотреть задание их на чертеже, а также возможности использова­ния в технике.

2. Линейчатые поверхности с тремя направляющими (группа аii).

Классификация линейчатых поверхностей и их распределение по группам и подгруппам в рамках общей схемы классификации поверх­ностей в зависимости от вида определителя, содержащего информацию о числе направляющих, показаны на рис. 3.

Из рис. 3 видно, что все многообразие линейчатых поверхностей может быть отнесено к трем группам:

группа А_II - линейчатые поверхности с тремя направляющими;

группа Б_II - линейчатые поверхности с двумя направляющими;

группа В_II - линейчатые поверхности с одной направляющей. Рас­смотрение линейчатых поверхностей начнем с группы А_II. Определитель этой наиболее общей группы линейчатых поверхностей имеет вид

Ф (; d₁, d₂ , d₃); [ { d₁, d₂ , d₃}  ];

где — прямая, образующая, d₁, d₂ , d₃ - направляющие.

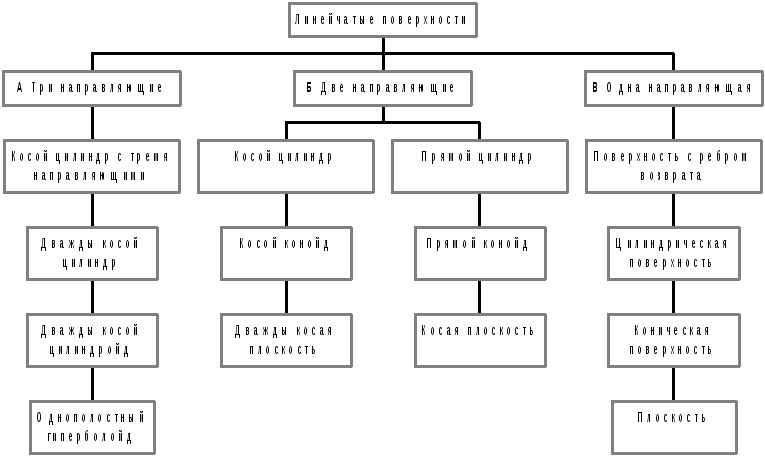
Рис. 3

Таблица 1. Линейчатые поверхности с тремя направляющими.

Группа А_II ; Ф (; d₁, d₂ , d₃); [ { d₁, d₂ , d₃}  ]

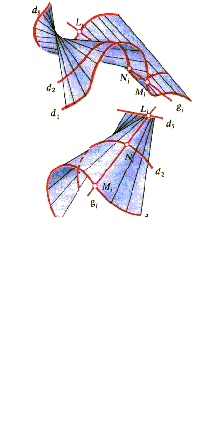
Рис. 4 Поверхность общего вида (косой

цилиндр с тремя направляющими )

Рис. 5 Дважды косой цилиндроид

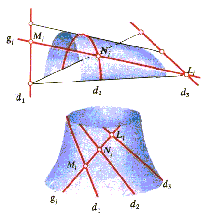
Рис. 6 Дважды косой коноид

Рис. 7 Однополостный гиперболоид

В зависимости от формы направляющих и их расположения в про­странстве можно получить различные поверхности этой группы, которые могут быть отнесены к четырем подгруппам (табл. 1, рис. 4 ... 7).

1. Поверхность косого цилиндра с тремя направляющими ( табл. 1, рис. 4). Эта поверхность может быть задана на эпюре Монжа проек­циями трех криволинейных направляющих и пересекающей их прямо­линейной образующей.

2. Поверхность дважды косого цилиндроида (см. табл. 4, рис.5). Она образуется в том случае, когда две из трех направляющих кривые, а третья — прямая линия. В инженерной практике находят примене­ние частные случаи поверхностей этого вида.

Поверхность косого клина. Эта поверхность получается в том слу­чае, когда все три направляющие расположены в параллельных плос­костях, причем криволинейные направляющие — гладкие кривые. По­верхность косого клина используется при конструировании поверхности. крыла летательного аппарата (рис. 8). При этом достигаются хорошие технологические условия изготовления его каркаса.

Поверхность косого перехода. Для образования поверхности ко­сого перехода в качестве криволинейных направляющих берут дуги окружностей одинакового радиуса, расположенные в параллельных плоскостях, а в качестве третьей направляющей — прямую, перпен­дикулярную к плоскостям окружностей и проходящую через середи­ну отрезка, который соединяет центры окружностей (рис. 9). Поверх­ности косого перехода применяются в архитектуре и строительной практике.

3. Поверхность дважды косого коноида (см. табл. 1, рис.6). Эта поверхность образуется в том случае, когда одна из трех направ­ляющих кривая, а две другие — прямые линии.

4. Поверхность однополостного гиперболоида (см. табл.1, рис.7). Поверхность однополостного гиперболоида может быть получена при движении прямолинейной образующей по трем скрещивающимся пря­мым, не параллельным одной плоскости.

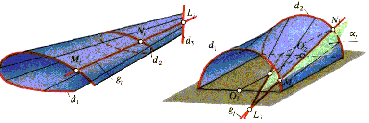
Рис. 8 Рис. 9

На рис. 10 поверхность однополостного гиперболоида задана пря­мыми направляющими , , показаны образующие , , . Определение положения образующей рассмотрим на примере пост­роения прямой . На направляющей , отмечаем произвольную точку 1 (1', 1").

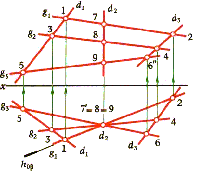
Рис. 10 Рис. 11

Эта точка совместно с направляющей (прямая для упрощения геометрических построений принята горизонтально проеци­рующей) определяет плоскость . Находим точку 2 =  h_{0 }.

Точки 1 и 2 определяют образующую . Аналогично находят проекции прямых , .

Поверхность однополостного гиперболоида обладает одним замеча­тельным свойством: направляющие , , можно принять за обра­зующие, а образующие , , считать направляющими, при этом получится та же самая поверхность, т.е. определители

Ф (; , , ); [ { , , }  ],

Ф (;, , ); [ { , , }  ]

тождественны. Иными словами, в однополостном гиперболоиде име­ются два семейства прямолинейных образующих, причем образую­щие одного семейства не пересекаются между собой, но каждая из образующих одного семейства пересекает все образующие другого семейства.

Можно представить случай, когда три прямолинейные образующие могут быть совмещены друг с другом путем вращения вокруг неко­торой оси. В этом случае вся поверхность может быть образована враще­нием только одной из трех образующих вокруг этой оси. Покажем, что при этом получается поверхность однополостного гиперболоида.

Пусть прямая g (рис. 11) вращается вокруг оси i (прямая g и ось i скрещиваются ). Приведем прямую а, пересекающую ось i в точке A. Прямые а и i определяют меридиональную плоскость поверхности, которая образуется вращением прямой g, При вращении прямой а вок­руг оси i образуется коническая поверхность вращения, заданная на чертеже двумя положениями образующей а₁ , а₂ и осью i. Прямая g, не параллельная этой конической поверхности, пересечет ее в двух точках. Допустим, что этими точками будут М и N. При вращении прямая g пересечет прямые а₁ и а₂ в точках М₁,N₁ и М₂,,N₂, т.е. произвольная прямая меридиональной плоскости пересекает меридиан поверхности в двух точках. Это говорит о том, что меридиан этой поверхности — кри­вая второго порядка.

Ось i меридиана не пересекает, но является для него осью симмет­рии. Это, в свою очередь, говорит о том, что меридиан поверхности — кривая второго порядка - гипербола, а прямая i - ее мнимая ось. Мы показали, что в частном случае линейчатая поверхность с тремя скрещи­вающимися прямолинейными направляющими пересекается плоскостью, проходящей через ось поверхности, по гиперболе; отсюда и произошло название этой поверхности - однополостный гиперболоид вращения. Плоскость, перпендикулярная к оси однополостного гиперболоида, пересекает его по эллипсу, и частном случае — по окружности (при пересечении однополостного гиперболоида вращения).

Практически для построения проекций однополостного гиперболои­да вращения необходимо: построить проекции двух окружностей, распо­ложенных в двух параллельных плоскостях; разделить проекции окруж­ностей на произвольное равное число частей (рис. 12); затем соединить прямой линией точку 1₁” нижней окружности с любой (кроме 1₂”) точкой верхней окружности. Па чертеже 12 точка 1₁” соединена с точкой 3₂”, точ­ка 2₁” с 4₂” и т.д. Соединив все точки деления нижней окружности с точ­ками деления верхней окружности, получим проекции каркаса

Рис. 12

поверх­ности. Второе семейство линий каркаса этой поверхности может быть образовано, если соединить первую точку верхней окружности с третьей точкой нижней окружности (1₁” с 3₁”) точку 2₂” с точкой 4₁”, 3₂” с 5₁” и т.д.

Поверхность однополостного гиперболоида вращения широко ис­пользуется в технике, в частности, для передачи вращения при скре­щивающихся осях с помощью зубчатых или фрикционных гипербоидальных колес. Особенно широкое применение эта поверхность нашла в строительстве. Одним из примеров может служить башня Шухова, построенная в Москве для установки антенны радиостанции "Комин­терн" - первой мощной радиостанции в Советском Союзе.

Гиперболический параболоид. В частном случае, когда прямолиней­ная образующая скользит по трем скрещивающимся прямым (нап­равляющим), параллельным одной плоскости, получается поверхность, называемая гиперболическим параболоидом. Такому названию эта поверхность обязана тем, что при пересечении ее плоскостями в сече­ниях получаются гипербола и парабола.

Поверхность гиперболического параболоида обладает одним заме­чательным свойством, состоящим в том, что не только ее направляю­щие параллельны одной плоскости, но и образующие, скользящие по этим направляющим, также параллельны некоторой плоскости.