ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
КУМЕРТАУСКИЙ ФИЛИАЛ
Кафедра «Промышленная автоматика»
КУРСОВАЯ РАБОТА
по дисциплине «Математические основы дискретной логической системы»
Вариант 10
Выполнил: студент гр. АТПП-209
Р. С. Кутушев
Проверил: ст. преподаватель
А.Р. Фаткуллин
Кумертау – 2008
Содержание
Введение
Традиционно к дискретной математике относят такие области математического знания, как комбинаторика, теория чисел, математическая логика, теория алгебраических систем, теория графов и сетей и т.д. Дискретная математика всегда оставалась наиболее динамичной областью знаний. Сегодня наиболее значимой областью применения методов дискретной математики является область компьютерных технологий. Это объясняется необходимостью создания и эксплуатации электронных вычислительных машин, средств передачи и обработки информации, автоматизированных систем управления и проектирования. На грани дискретной математики и программирования появляются новые дисциплины, такие как разработка и анализ вычислительных алгоритмов, нечисленное программирование, комбинаторные алгоритмы, алгоритмизация процессов. Дискретная математика и примыкающие к ней дисциплины изучаются во всех университетах и институтах, где осуществляется подготовка специалистов в области программирования, математики, а также по экономическим, техническим и гуманитарным направлениям.
Задание № 1
Доказать, что:
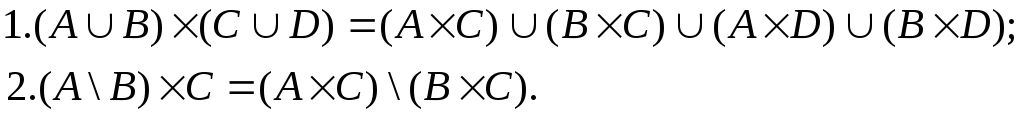
Решение для первого уравнения.
Решение для второго уравнения.
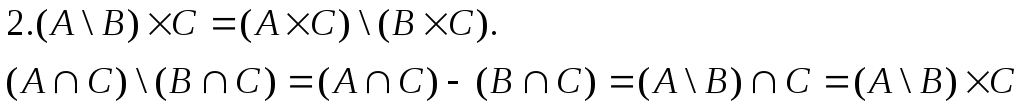
Задание № 2
При каких условиях на А и В выполняется равенство (А\В) U В = А.
Решение:
В U (А\В) = В ∩ (А U В) = А (1)
В U (А\В) = (В U А) \ (В U В) = В ∩ (А\В)
Отсюда доказать что В ∩ (А U В) = А Если Х є В ∩ (А U В), то
Х є В ∩ Х є А U В и, следовательно,
В ∩ (А U
В)
А
(2)
Если же Х є В, то Х є А U В, а значит, Х є В ∩ (А U В), т.е.
А
В ∩ (А U
В).
(3)
Из (2) и (3) следует второе из равенств (1).
Задание № 3
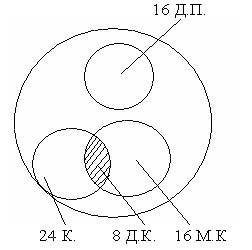
На экскурсии были семиклассники и восьмиклассники. Все они были либо с комсомольцами значками, либо в пионерских галстуках. Мальчиков – комсомольцев было 16, а комсомольцев 24, девочек – пионерок было ровно столько, сколь мальчиков – комсомольцев. Сколько учащихся было на экскурсии?
Решение:
а) определим число девочек комсомольцев
24 – 16 = 8
б) определим, сколько всего учащихся было на экскурсии.
24 + 16 = 40
Задание № 5
Представить в СДНФ
следующие функции
:
а) с помощью таблицы истинности;
б) с помощью эквивалентных преобразований:
1.
2.
а) представим
функцию
в СДНФ, с помощью таблицы истинности.
|
|
x1 |
x2 |
x3 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
2 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
|
3 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
|
6 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
|
7 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
Из значения функции выбираем элементы равные единице и выписываем соответствующие им комбинации значений х.
Этими комбинациями являются: (000), (001), (010), (011), (101), (110), (111). Исходя из полученных значений комбинаций, составляем СДНФ.
Путем
замены х
с нулевыми значениями на их отрицания,
переходим к нормальному виду СДНФ.
а) представим
функцию
в СДНФ, с помощью таблицы истинности.
|
|
x1 |
x2 |
x3 |
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
|
2 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
|
3 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
|
4 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
|
6 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
|
7 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
Из значения функции выбираем элементы равные единице и выписываем соответствующие им комбинации значений х.
Этими комбинациями являются: (101), (110). Исходя из полученных значений комбинаций, составляем СДНФ.
Путем замены х с нулевыми значениями на их отрицания, переходим к нормальному виду СДНФ.
Задание № 7
Методом неопределенных
коэффициентов найти полиномы Жегалкина
для следующих функций:
Этот метод применяется если функция задана в виде таблицы.
Решение:
Составим таблицу истинности
|
|
Подставляем
полученные данные в формулу общего вида
полинома Жегалкина. Решение имеет вид:
Задание № 8
Методом треугольника
Паскаля построить полином Жегалкина
для этой функции, если:
Решение:
Многочлен Жегалкина можно получить с помощью треугольника Паскаля по единицам его левой стороны.
Составляем таблицу истинности и строим треугольник Паскаля.
|
x1 |
x2 |
x3 |
x4 |
|
∆ Паскаля |
|
|
0 |
0 |
0 |
0 |
0 |
0 0 1 1 1 1 1 0 0 1 0 1 0 1 0 0 |
0 |
|
0 |
0 |
0 |
1 |
0 |
0 1 0 0 0 0 1 0 1 1 1 1 1 1 0 |
0 |
|
0 |
0 |
1 |
0 |
1 |
1 1 0 0 0 1 1 1 0 0 0 0 0 1 |
1 |
|
0 |
0 |
1 |
1 |
1 |
0 1 0 0 1 0 0 1 0 0 0 0 1 |
0 |
|
0 |
1 |
0 |
0 |
1 |
1 1 0 1 1 0 1 1 0 0 0 1 |
1 |
|
0 |
1 |
0 |
1 |
0 |
0 1 1 0 1 1 0 1 0 0 1 |
0 |
|
0 |
1 |
1 |
0 |
0 |
1 0 1 1 0 1 1 1 0 1 |
1 |
|
0 |
1 |
1 |
1 |
0 |
1 1 0 1 1 0 0 1 1 |
1 |
|
1 |
0 |
0 |
0 |
0 |
0 1 1 0 1 0 1 0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
1 0 1 1 1 1 1 |
1 |
|
1 |
0 |
1 |
0 |
0 |
1 1 0 0 0 0 |
1 |
|
1 |
0 |
1 |
1 |
1 |
0 1 0 0 0 |
0 |
|
1 |
1 |
0 |
0 |
0 |
1 1 0 0 |
1 |
|
1 |
1 |
0 |
1 |
1 |
0 1 0 |
0 |
|
1 |
1 |
1 |
0 |
1 |
1 1 |
1 |
|
1 |
1 |
1 |
1 |
1 |
0 |
0 |
Левая сторона содержит 8 единиц, поэтому полином Жегалкина будем составлять из 9 слагаемых.
Решение имеет вид:
