Медленные активационные межфазные переходы

Теперь рассмотрим более медленные конформационные переходы, связанные с крупномасштабными изменениями, с деформацией белковой структуры, которые часто связаны с преодолением энергетического барьера, подобного барьеру, разделяющему две фазы при фазовых переходах I рода. Как уже указывалось этот барьер отличается от активационного барьера, так как имеет как энергетическую, так и энтропийную составляющие (т.1, с.176–180). Например, барьер может создаваться за счет уменьшения энтропии при сближении и реакции между отдаленными участками цепи.

Рассмотрим самый простой случай (рис.3–92 а) перехода системы, состоящей из n молекул, из состояния 0 в состояние 1, когда отсутствуют кинетические ловушки (состояния более стабильные, чем исходное состояние 0, но менее стабильные, чем конечное состояние 1), типа стабильного интермедиата L (б), или типа побочной ловушки O (в).

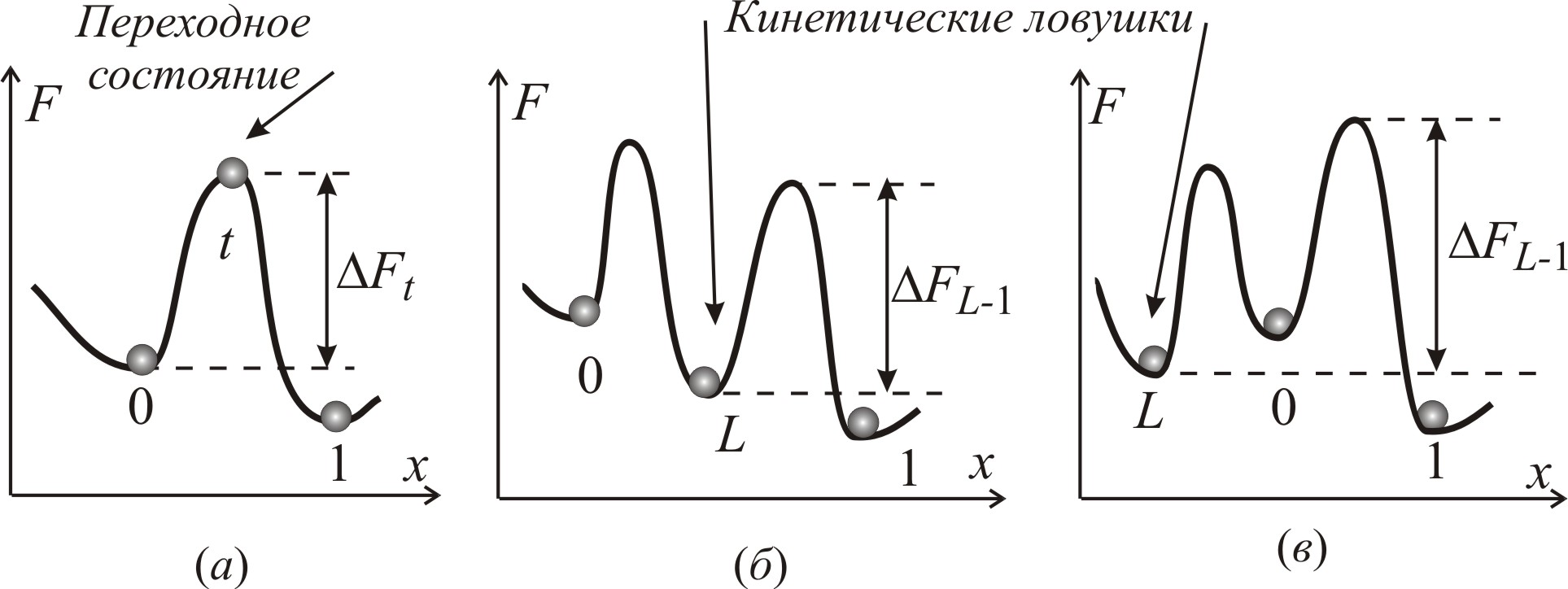
Рис. 3–92. Преодоление энергетического барьера (а) в отсутствие кинетических ловушек L и при их наличии (б, в). – высота энергетического барьера: свободная энергия переходного состояния (а); – высота барьера при переходе из ловушки в конечное состояние, отсчитываемая от энергии самого глубокого из всех предшествующих состояний (б, в). х – координата реакции

Скорость процесса 0→1 в случае (а) определяется, во-первых, населенностью переходного состояния, то есть числом молекул , энергия которых в результате конформационных переходов превышает энергию молекул в состоянии 0 на величину , и, во-вторых, скоростью перехода из этого состояния t в забарьерное состояние 1. Среднее число молекул в состоянии t согласно распределению Больцмана описывается выражением:

(3.24)

Здесь – сводная энергия барьера, отсчитанная от энергии исходного состояния 0, причем . Пусть τ – время перехода молекулы из переходного состояния t в состояние 1. Скоростью перехода 0→1 называется величина, обратная времени перехода , необходимого для перехода всех n частиц из состояния 0 в состояние 1. Поскольку за время τ все молекулы, находящиеся в переходном состоянии, перейдут в состояние 1, то перехода всех частиц можно оценить по формуле

(3.25)

и . (3.26)

При наличии ловушки (рис.3–92 б) общее время находится как сумма: , причем всегда отсчитывается от энергии состояния 0.

Перенос лигандов в белковых молекулах

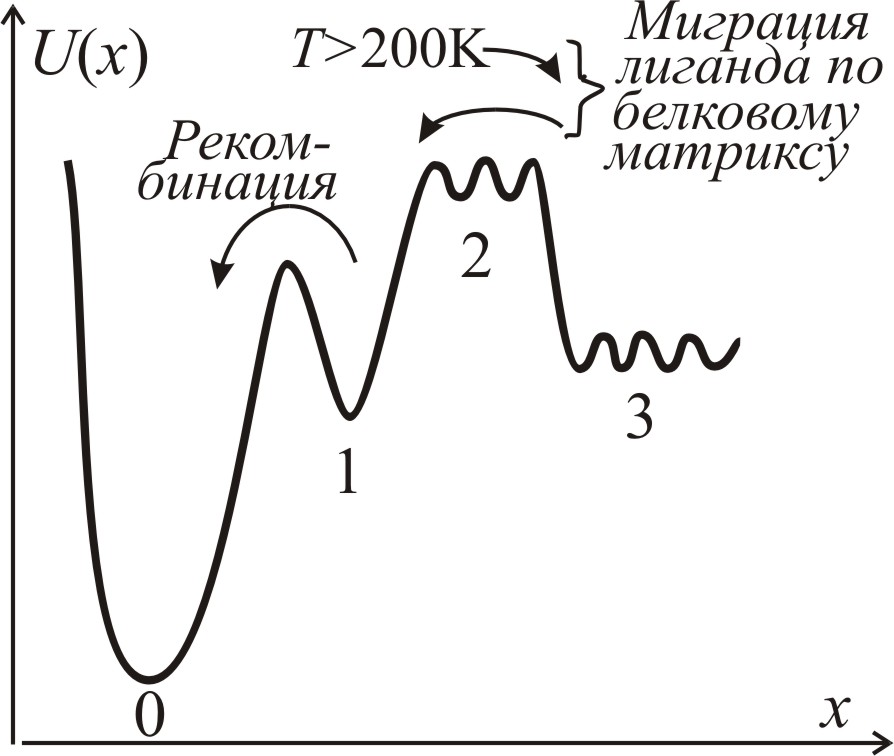
Ограниченные структурные флуктуации обеспечивают возможность переноса лигандов внутри белковых молекул. Иллюстрацией может служить конформационные смещения белковых групп внутри молекулы миоглобина, которые обеспечивают возможность диффузионного движения лигандов внутри матрицы белка. Наиболее изучен в настоящее время процесс связывания моноокиси углерода СО с атомом железа гемовой группы миоглобина Mb. На рис. 3–93 схематически представлен энергетический профиль состояний лиганда СО: 0 – связанное состояние СО с гемовым железом миоглобина (MbСО), 1 – СО в гидрофобном кармане гема, 2 – в белковой матрице, 3 – в растворителе.

Рис. 3–93. Энергетический профиль состояний окиси углерода в миоглобине: в связанном с гемовым железом (0), в гемовом кармане (после фотодиссоциации) (1), в матриксе белка (2), в растворителе (вне белка) (3). Стрелками показаны процессы рекомбинации (связывания) СО с гемовым железом миоглобина (1→0) и процессы миграции лиганда по белковому матриксу. При Т>200 К происходит растормаживание конформационных флуктуаций белкового матрикса и появляется возможность для выхода лиганда из гемового кармана (1) в растворитель (3). х – координата реакции

Гемовый карман образован в основном гидрофобными аминокислотами. Он имеет размер порядка 5Å. Вход в гемовый карман блокируется пропионовой кислотой гема. На краю гемового кармана локализован атом железа.

Рассмотрим сначала процесс выхода СО из гемового кармана (0) в растворитель (3). Если подвергнуть миоглобин со связанной моноокисью углерода СО действию лазерного облучения, то происходит фотодиссоциация: разрыв связи СО с гемовым железом. После фотодиссоциации лиганд находится между двумя энергетическими барьерами (состояние 1 на рис. 3–93). Если преодолевается барьер связывания с железом, то происходит процесс рекомбинации, преобладающий при температурах ниже 200 К. Выше 210 К, за счет конформационных флуктуаций белковой матрицы, значительно возрастает вероятность выхода лиганда из молекулы белка в растворитель.

Торсионные (винтовые) вращения боковых цепей гистидина Е7, валина Е11 и тирозина Е10 (рис. 3–56, с.428), требующие затрат энергии (30÷45)кДж/моль, создают возможность движения лиганда по системе локальных минимумов, разделенных потенциальными барьерами ~20 кДж/моль и, таким образом открывают энергетические «долины» для диффузии лиганда в белке при обычных температурах.

Обратный процесс движения СО из растворителя в гемовый карман показан стрелками на рис. 3–93. Кинетика проникновения (диффузии) лигандов в гемовый карман может быть описана в рамках теории диффузии в вязких жидкостях, когда скорость диффузии определяется энергией образования полостей (дырок) в вязкой среде. В жидкостях среднее время ожидания возникновения дырки составляет величину порядка , где E_A – энергия образования (активации) дырки, ₀ ~ 10^–13 c – характерное время колебаний молекул около локального положения равновесия.

Будем считать, что энергия активации при движении лиганда в системе локальных минимумов, возникающих в результате конформационной подвижности белка, составляет ~20 кДж/моль. При обычных функциональных температурах (~36°) . Тогда, полагая , находим , то есть диффузия происходит достаточно быстро.