Быстрые тепловые конформационные переходы

Для описания кинетики динамической подвижности белков можно использовать модифицированную модель диффузионного движения молекул в жидкости (см. ч.III, с. 215–217). Напомним, что диффузионное движение молекулы в жидкости складывается из ее колебательного (с частотой ₀) движения в потенциальной яме, создаваемой молекулами, окружающими данную молекулу, и перескоков с характерной частотой _п из одного равновесного положения в другое – образующуюся рядом флуктуационную полость.

Однако, в отличие от жидкостей диффузионное движение жестких фрагментов белков в вязкой среде имеет ряд принципиальных особенностей.

1. Атомы в каждом фрагменте ковалентно связаны и совершают высокочастотные колебания, соответствующие внутренним степеням свободы, с малыми амплитудами, как в обычных молекулах. Поскольку пространственная структура белка гетерогенна, то различные фрагменты обладают различными подвижностями, отличающимися характерными временами и амплитудами смещений. При переходе белковой глобулы из одного конформационного состояния в другое, фрагменты белка смещаются в определенных направлениях на расстояния порядка 0,1 нм. Смещения каждого фрагмента принято описывать конформационной координатой х. Так как предельная величина смещения ограничена, то фрагменты при конформационном переходе смещаются лишь в ограниченной области пространства.

2. Фрагменты в цепи белка связаны ковалентными связями и поэтому не могут перемещаться независимо. Смещение отдельного фрагмента в направлении х вызывает деформацию цепи и возникновение упругой силы F_упр(x), стремящейся вернуть фрагмент в первоначальное положение. Поскольку всякая сила связана с изменением потенциальной энергии системы, то удобно ввести конформационный потенциал , связанный с силой F_упр(x) соотношением:

. (3.15)

Конформационный потенциал описывает форму потенциальной ямы для данного фрагмента, в которой он совершает ограниченное движение при переходе белка из одной конформации в другую. В общем виде зависимость имеет вид:

. (3.16)

Для квадратичной зависимости U(x) коэффициент .

3. Если бы фрагмент мог свободно перемещаться в пространстве, то переход из состояния с конформационной координатой ( ) в состояние с координатой ( ) совершался бы, при соответствующей температуре, по горизонтальной прямой (см. рис. 3–91). Но, поскольку среднее расстояние между фрагментами в белковой молекуле и амплитуда колебаний атомов внутри фрагментов существенно меньше , то переход по прямой линии невозможен.

Чтобы некоторый фрагмент белка мог переместиться как целое на расстояние нм (превышающее амплитуду колебаний составляющих его атомов (0,01÷0,1)Å), рядом должна образоваться полость в результате флуктуационных смещений молекулярных групп, окружающих данный фрагмент, то есть перемещение фрагмента имеет диффузионный характер. Поэтому реально переход фрагмента между состояниями и может осуществляться путем серии термически активированных перескоков между локальными потенциальными ямами, в которых фрагменты белка совершают колебательное движение с собственными частотами в течение времени между двумя последовательными перескоками. Прыжковая диффузия по локальным конформационным подсостояниям (обозначенными светлыми точками) иллюстрируется рис. 3–91.

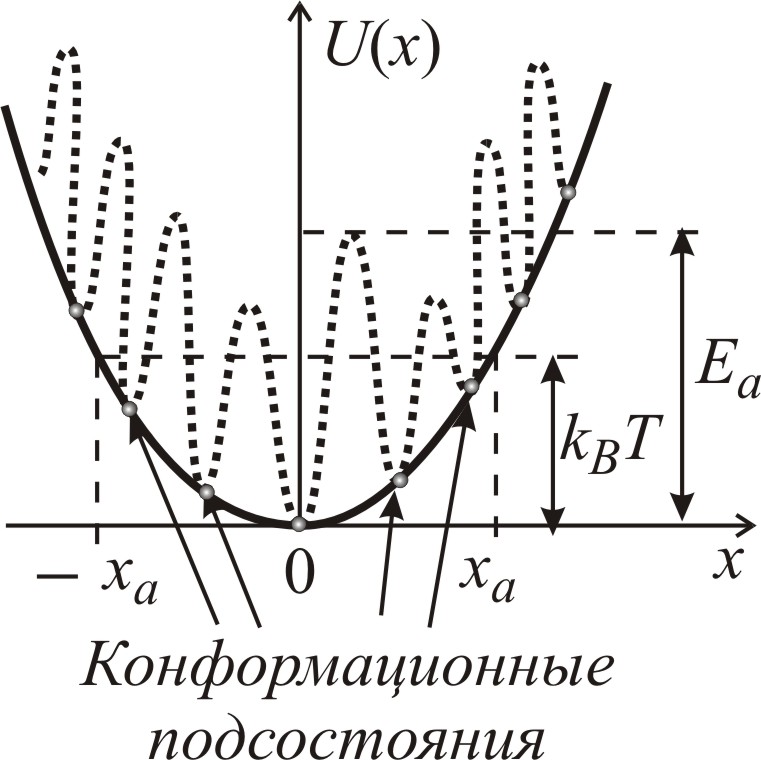
Чтобы переместиться из одного конформационного подсостояния в другое, фрагмент должен израсходовать часть своей кинетической энергии для смещения соседних групп. Следовательно, для движения фрагмента требуется энергия активации Е_а. Таким образом, движение фрагмента представляет сбой последовательное преодоление локальных потенциальных барьеров.

Рис. 3–91. Профиль потенциальной энергии U(x) (сплошная линия). Флуктуации энергии (пунктир) приводят к образованию локальных минимумов и барьеров, высота Еа и положение которых флуктуируют за счет взаимодействия с другими степенями свободы. ха – среднеквадратичная амплитуда ограниченной диффузии при температуре Т

Отсюда следует, что движение фрагмента характеризуется двумя пространственными масштабами. Во-первых, – микросмещениями между конформационными подсостояниями, происходящими при благоприятном перемещении соседних групп белка. Это диффузионное движение характеризуется коэффициентом конформационной диффузии D(x), зависящим от конфигурации окружающей среды. Здесь х – конформационная координата, указывающая положение системы на пути конформационных преобразований. Второй пространственный масштаб ( ) характеризует существенно более медленную перестройку конформации белковой молекулы при переходе из одного биологически активного состояния ( ) в другое ( ). Такой перестройке соответствует движение всей системы вдоль конформационной координаты – оси реакции – по профилю плавно изменяющегося конформационного потенциала U(x) (рис. 3–91).

4. Учтем теперь, что конформационные перестройки белковых макромолекул происходят в жидкой среде, которую можно характеризовать микровязкостью . При движении фрагментов в жидкой среде на них действует сила вязкого трения

, (3.17)

где – коэффициент силы вязкого трения, - скорость движения фрагментов. Коэффициенты и связаны соотношением Стокса

, (3.18)

где – эффективный линейный размер фрагмента (1÷10)Å.

Кроме силы терния на фрагменты действует сила , обусловленная столкновениями фрагментов с молекулами жидкости, как при броуновском движении:

, (3.19)

где – случайные моменты времени. Амплитуда силы также является случайной величиной.

С учетом всех, действующих на фрагмент сил, движение фрагмента описывается уравнением Ланжавена (M – масса фрагмента):

. (3.20)

Это стохастическое (вероятностное) уравнение, требующее задания функции распределения . Его решением также являются функции распределения: и .

Если считать, что для перехода макромолекулы из одного конформационного состояния в другое отдельные фрагменты должны сместиться в среднем на расстояние х₀, то зависимость от времени среднего квадратичного смещения фрагментов можно приближенно описать формулой

. (3.21)

Здесь – среднее квадратичное смещение, необходимое для перестройки белка, – время релаксации, определяющееся величиной коэффициента трения или микровязкостью среды:

, (3.22)

Из (2) следует, что при t = 0 смещение равно нулю , а при смещение стремится к среднему значению .

Поскольку микровязкость белка экспоненциально зависит от температуры

, (3.23)

где Е_а – энергия активации вязкого движения), то время релаксации экспоненциально уменьшается при повышении температуры. Соответственно скорость диффузии при повышении температуры увеличивается, и, наоборот, при понижении температуры – замедляется.

Для белков при Т = 300 К коэффициент вязкости составляет , что много больше вязкости воды ( ), средней вязкости биологической мембраны (0,1÷1)Па∙с и вязкости глицерина ( ); энергия активации ; среднеквадратичная амплитуда смещения .

Элементы вторичной структуры белков ( и ) совершают ограниченное диффузионное движение со средней амплитудой, зависящей от их массы и микровязкости среды. Амплитуда изгибных флуктуаций -спиралей достигает нескольких ангстрем.