МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ЭКОНОМИКИ И УПРАВЛЕНИЯ «НИНХ»

Институт заочного обучения

Кафедра ___________________________

Контрольная работа

Учебная дисциплина: Экономико-математические методы и модели

Номер варианта контрольной работы: №1245

Наименование направления (специальности, профиля подготовки):

Менеджмент организации

Ф.И.О студента: Сай Анастасия Сергеевна

Номер группы: МОП12

Номер зачетной книжки: 111938

Дата регистрации контрольной работы кафедрой ____________

Проверил:________________________________

(Ф.И.О.)

Оценочное заключение:

Новосибирск 2013

Оглавление

Задача 1 2

Задача 3 7

Задача 4 15

Задача 5 20

Задача 6 24

Задача 1

Для изготовления продукции двух видов А и Б предприятие расходует ресурсы, а от реализации этой продукции получает доход. Информация о нормах затрат ресурсов на единицу выпускаемой продукции, запасах расходуемых ресурсов, имеющихся в распоряжении предприятия, и выручки от реализации готовой продукции приведены в таблице:

Наименование ресурсов	Норма затрат на		Объем
	Продукт А	Продукт Б	ресурса
Сырье (кг)	3	1	277
Оборудование (ст.час)	1	2	381
Трудоресурсы (чел.час)	7	1	537
Цена реализации (руб)	507	101

Задача предприятия заключается в том, чтобы разработать программу выпуска, обеспечивающую получение максимальной выручки от реализации готовой продукции.

Требуется:

1. Построить математическую модель оптимизации выпуска продукции в форме задачи линейного программирования.

2. Используя графический метод решения задачи линейного программирования, найти оптимальную программу выпуска продукции и максимум ожидаемой выручки.

3. Составив задачу, двойственную к задаче оптимизации выпуска продукции, найти ее оптимальное решение, используя условия «дополняющей нежесткости». Дать экономическую интерпретацию этого решения.

Решение:

1. Введем обозначения: 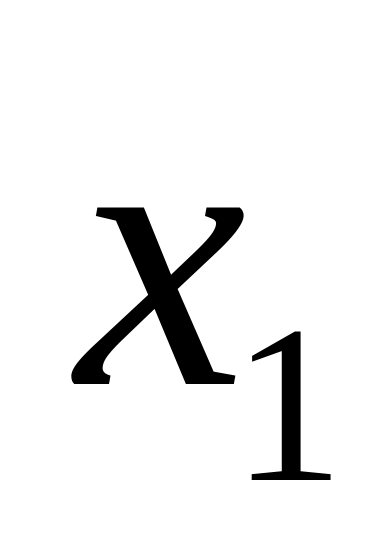- объем производства продукта А, - объем производства продукта Б. Условия и ограничения задачи:

• ограничения по использованию сырья:

• ограничения по использованию оборудования:

• ограничения по использованию трудоресурсов:

• Объемы производств не могут быть отрицательными: .

• Выручка предприятия:

Получили математическую модель оптимизации выпуска продукции в форме задачи линейного программирования:

2. Решим задачу графическим методом:

А

В

С

D

Градиент целевой функции: .

Так как нужно получить максимум целевой функции, то будем перемещать ее график в направлении градиента. Последней точкой пересечения графика целевой функции с областью допустимых решений OABCD будет точка С, то есть в этой точке целевая функция достигнет максимума. Эта точка является пересечением прямых и , найдем ее координаты:

Получили оптимальную программу выпуска:

,

Максимальное значение выручки, соответствующее этой программе:

(руб.)

3. Составим задачу, двойственную к задаче оптимизации выпуска продукции:

Найдем решение двойственной задачи через решение исходной, пользуясь условием «дополняющей нежесткости»:

При оптимальных значениях , система примет вид:

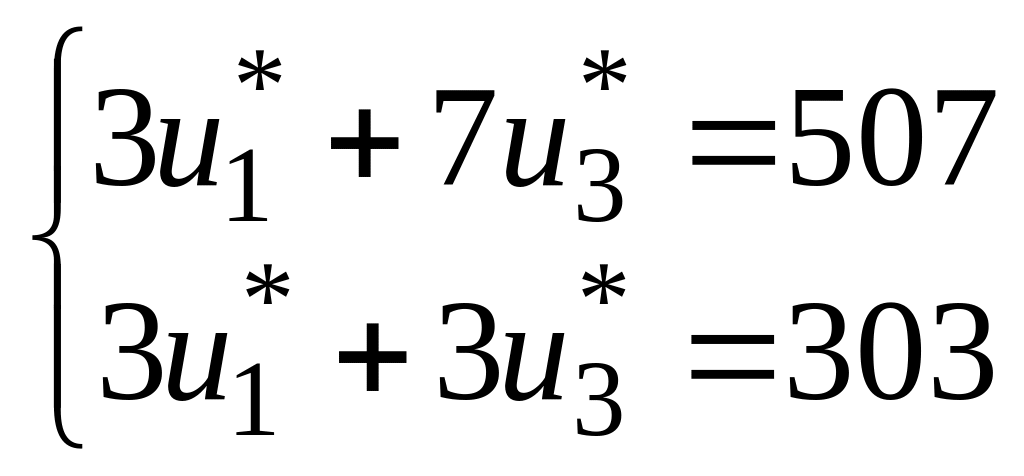
Получили оптимальное решение , , , .

Дадим экономическую интерпретацию полученного решения. Переменные , и обозначают условные двойственные оценки единицы ресурсов. Оценки и не равны нулю, значит, сырье и трудовые ресурсы полностью используются при оптимальном плане производства продукции. Двойственная оценка оборудования равна нулю, значит, этот ресурс не полностью используется при оптимальном плане производства продукции. Увеличение месячных запасов сырья на 1 кг увеличит максимальную суммарную выручку на 50 рублей. Увеличение месячного фонда трудовых ресурсов на 1 чел. час увеличит максимальную суммарную выручку на 51 рубль.

Предприятию целесообразно сократить объем используемого при производстве оборудования, но не более чем на станко-часов в месяц. Предприятию выгодно приобретение дополнительного сырья, если связанные с этим затраты не превышают 50 руб. за 1 кг. Предприятию выгодно увеличение трудовых ресурсов, если затраты на эти ресурсы не будут превышать 51 руб. за один человеко-час.