2.2. Приложение определённого интеграла
а) Вычисление площадей плоских фигур.
П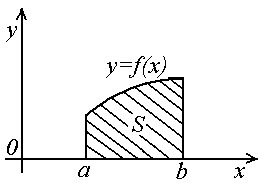
лощадь
криволинейной трапеции, ограничена
прямыми x
= a,
x
= b,
(a
< b),
осью ox
и непрерывной кривой
.
Вычисляется по формуле
(4)
П
a
b
xy = 4; x+y=5
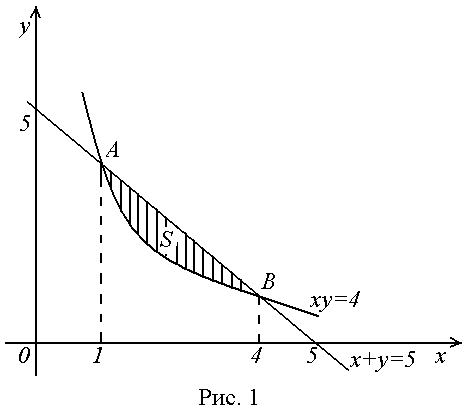
Решение: Построим область S (рис.4) и найдём абсциссы точек пересечения А, В:
Пример 5.
Найти площадь области, ограниченной
линиями
.
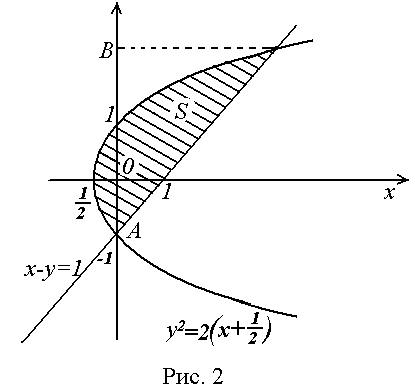
Решение: Построим область S (рис.2) и найдём ординаты точек пересечения А, В:
2.3 Несобственные интервалы.
Пример:
,
чего не может быть, так как интеграл от
положительной функции должен быть
положительным. Ошибка от незаконного
применения формулы Ньютона-Лейбница.
Действительно,
при х=0
не является непрерывной
.
Понятие определённого интеграла дано для конечного отрезка и непрерывной на нём функции . Оно теряет смысл, если интервал интегрирования бесконечен или функция в интервале интегрирования имеет точки разрыва 2го рода.
Интеграл называется несобственным, если функция не ограничена на , или неограниченна сама область интегрирования.
2.4. Интегралы с бесконечными пределами (I рода)
Е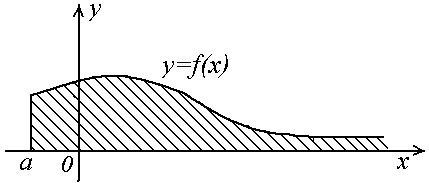
сли
f(x)
непрерывна,
,
то по определению
(3.1)
Если существует конечный предел в правой части формулы (3.1.), то несобственный интеграл называется сходящимся, если же этот предел бесконечен, или не существует, то – расходящимся и значения не имеет.
Аналогично определяются интегралы:
Если оба предела в правой части конечны, то интеграл называется сходящимся, если же хотя бы один из них бесконечный или не существует, то – расходящимся.
Итак, несобственные интегралы с бесконечными пределами – пределы определённых интегралов с переменными верхними или нижними пределами при стремлении этих пределов к бесконечности.
Вычислить несобственные интегралы, или установить их расходимость:
интеграл сходится и его значение равно 1.
интеграл расходится и значений не имеет
-
предел не существует
интеграл расходится.
2.5. Интегралы от неограниченных функций (II рода)
Р
ассмотрим
функции с бесконечными разрывами на
отрезке
.
Пусть функция
непрерывна
в точке x
=
b
– разрыв 2го
рода, т.е.
,
то по
определению
(1)
Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, а если он не существует или равен бесконечности, то интеграл называется расходящимся.
А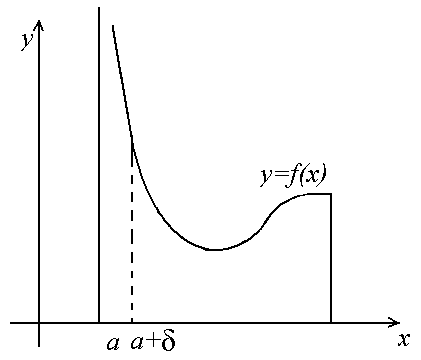
налогично
определяются интегралы:
а)
- непрерывна
,
,
то по определению
(2)
б)
f(x)
терпит разрыв 2го рода в точке x=c,
(a<c<b).
Тогда по
определению: (3)
ε и δ стремятся к нулю произвольно, независимо друг от друга.
Если хотя бы один из пределов правой части (3) бесконечен, или не существует, то интеграл называется расходящимся и значения не имеет, в противном случае – сходящимся.
Вычислить несобственные интегралы или установить их расходимость:
б) Геометрический смысл несобственного интеграла от неограниченных функции.
Если несобственные интегралы II рода сходятся, то они определяют площадь криволинейной трапеции с бесконечной высотой.