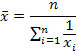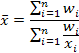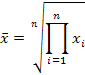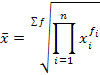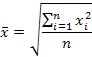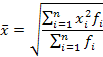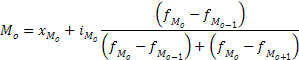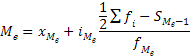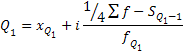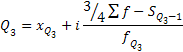3.3 Построение средних величин
3.3.1 Виды средних величин
Формулы для расчета степенных средних можно представить в виде следующей таблицы:
Наименование |
Формула |
Условия применения |
средняя гармоническая простая |
|
(k=-1) вычисляется в тех случаях, когда приходится суммировать не сами варианты, а обратные им величины |
средняя гармоническая взвешенная |
|
|
средняя геометрическая простая |
|
(k=0) используется в тех случаях, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин |
средняя геометрическая взвешенная |
|
|
средняя арифметическая простая |
|
(k=1) исчисляется в тех случаях, когда объем варьирующего признака для всей совокупности образуется как сумма значений признака отдельных ее единиц |
средняя арифметическая взвешенная |
|
|
средняя квадратическся простая |
|
(k=2) применяется в тех случаях, если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин |
средняя квадратическся взвешенная |
|
Формулы для расчета структурных средних можно представить в виде следующей таблицы:
Наименование |
Формула |
Мода в дискретном ряду |
варианта с наибольшей частотой |
Мода в интервальном ряду |
|
Медиана в дискретном ряду |
признак приходящееся на середину упорядоченной (ранжированной) совокупности |
Медиана в интервальном ряду |
|
Нижний квартиль |
|
Верхний квартиль |
|
где: 
-
нижняя граница модального интервала;
-
величина модального интервала;
-
частота модального интервала;
-
частота следующая за модальным интервалом;
-
частота предшествующая модальному
интервалу;
-
начальное значение медианного интервала;
-
величина модального интервала;
-
сумма частот ряда;
-
накопленная частота интервала
предшествующая медианному интервалу;
-
частота медианного интервала;
- нижняя граница интервала, содержащего
нижний (верхний) квартиль;
i - величина интервала;
- накопленная частота интервала,
предшествующего интервалу, содержащему
нижний (верхний) квартиль;
- частота интервала, содержащего нижний
(верхний) квартиль.
3.3.2 Типовой пример со средними величинами
В качестве примера рассмотрим динамику валового сбора зерна (в весе после доработки, в хозяйствах всех категорий; тысяч тонн) по Южному федеральному округу
Субъекты |
2005 |
2006 |
2007 |
2008 |
2009 |
2010 |
Южный федеральный округ |
18796,4 |
18539,4 |
15556,0 |
26709,2 |
20322,2 |
18818,8 |
Республика Адыгея |
303,6 |
302,3 |
383,5 |
543,0 |
471,5 |
437,5 |
Республика Калмыкия |
343,8 |
359,5 |
170,2 |
437,4 |
401,5 |
275,4 |
Краснодарский край |
8257,9 |
8196,4 |
8103,8 |
11634,4 |
9486,0 |
9942,6 |
Астраханская область |
42,7 |
39,0 |
29,6 |
40,2 |
48,1 |
43,6 |
Волгоградская область |
3581,4 |
3334,9 |
2774,1 |
5183,2 |
3317,1 |
1498,7 |
Ростовская область |
6266,9 |
6307,2 |
4094,8 |
8871,1 |
6598,0 |
6620,9 |
Вначале оценим средний валовой сбор за весь период по каждому субъекту:
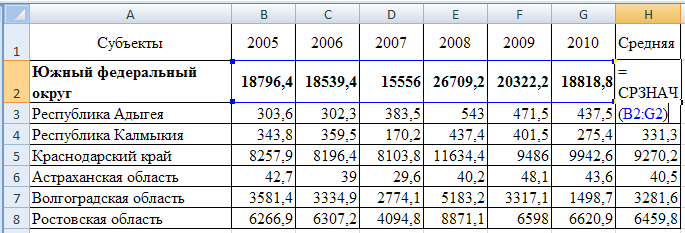
Рисунок 3.5 – Результаты оценок среднего валового сбора для каждого субъекта
Согласно приведенным данным, лидером в данном округе является Краснодарский край со средним валовым сбором за период 9270 тыс. тонн.
Если перейти к относительному показателю динамики (цепная схема), то можно оценить среднею геометрическую:
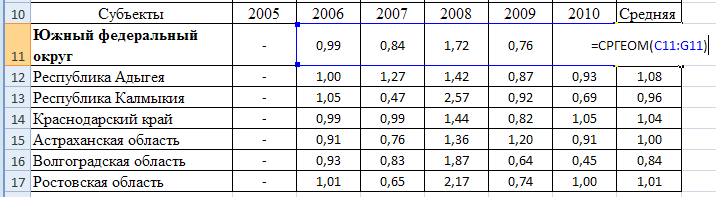
Рисунок 3.6 – Результаты оценок относительного показателя динамики (темпа роста) валового сбора для каждого субъекта
Наибольший средний темп роста наблюдается все также у Краснодарского края – 4 % в год.