Лекция IV-Д-3

Глава VIII. Теоремы об изменении количества движения материальной точки и количества движения механической системы

§ 46. Импульс силы и его проекции на координатные оси

Если постоянная по модулю и направлению сила действует в течение промежутка времени то ее импульсом за этот промежуток времени является вектор (46.1)

Направление этого вектора совпадает с направлением силы, а его модуль равен произведению модуля силы на время ее действия.

Импульс силы характеризует передачу материальной точке механического движения со стороны действующих на нее тел за данный промежуток времени.

Единицами импульса являются: в системе МКС импульс силы в один ньютон за время в одну секунду, т. е. один ньютон секунда (кг∙м/с), в системе СГС - одна дина∙секунда (г∙см/с), а в системе МКГСС—1 кгс∙с, в системе СИ: 1 Н∙сек.

Чтобы найти импульс переменной силы за промежуток времени , этот промежуток разбивают на п элементарных промежутков и определяют элементарные импульсы силы за эти промежутки. Модуль элементарного импульса равен произведению модуля силы в момент на , а направление совпадает с направлением силы в этот момент (рис. 107): (46.2)

И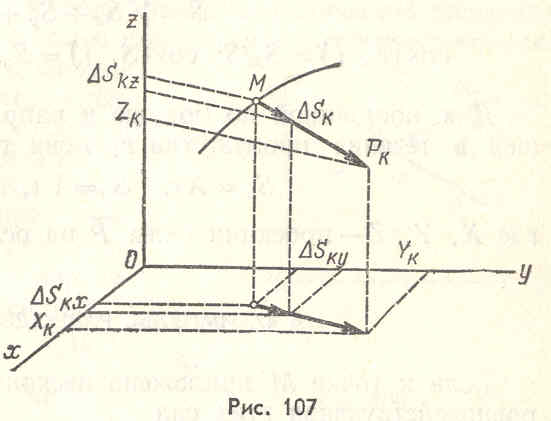 мпульс силы за промежуток определяется как предел геометрической суммы элементарных импульсов при и при :

Предел векторной суммы бесчисленного множества бесконечно малых слагаемых при называется векторным интегралом от вектора по скалярному аргументу t. Таким образом, (46.3)

Модуль и направление импульса переменной силы можно определить по способу проекций. Импульс переменной силы за промежуток времени представляет собой предел геометрической суммы элементарных импульсов . Поэтому проекция импульса на каждую координатную ось равна пределу алгебраической суммы проекций элементарных импульсов на эту ось.

Проекции элементарного импульса на оси координат (рис. 107):

;

аналогично

, ,

где - проекции силы на оси координат.

Просуммировав проекции элементарных импульсов и перейдя к пределу, получим определенные интегралы по переменной , представляющие собой проекции импульса на оси координат:

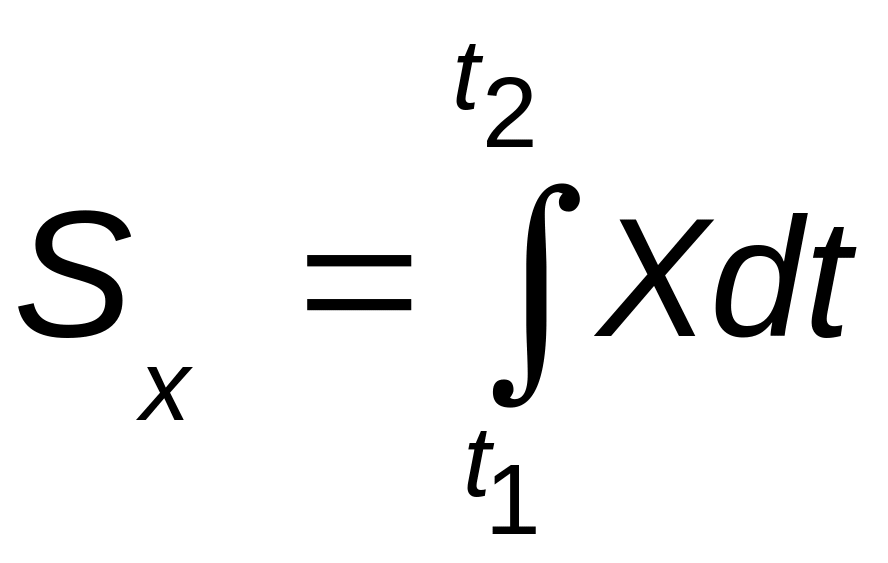, , . (46.4)

Здесь X = f₁(t); Y = f₂(t); Z = f₃(t) — проекции переменной силы на оси координат.

Модуль и направление импульса определяются по его проекциям:

cos(S, i) = S_X/S; cos(S, j)=S_y/S; cos (S, k)=S_z/S. (46.5)

Для постоянной по модулю и направлению силы , действующей в течение промежутка времени τ, формулы (46.4) имеют вид , (46.6)

где X, Y, Z — проекции силы на оси координат.

Покажем доказательство теоремы импульсов по методике профессора Фролова:

Умножим обе части уравнения № 5 на dt: или окончательно:

, где

- элементарный импульс k-той внешней силы, приложенный к материальной точке системы.

Импульс силы характеризует передачу материальной точке, посредством приложенной к ней силы , механического движения со стороны действующих на нее тел за данный промежуток времени . Направление вектора импульса силы совпадает с направлением приложенной к точке силы , а его модуль равен произведению модуля силы на время ее действия .

или

- элементарный импульс главного вектора внешних сил, приложенных к системе материальных точек;

Окончательно:

Теорема импульсов (механической системы):

Изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме элементарных импульсов внешних сил, приложенных к системе, за тот же промежуток времени.

Или, после приведения системы сил к ее Главному вектору:

(Изменение количества движения механической системы за некоторый промежуток времени равно элементарному импульсу Главного вектора внешних сил, приложенных к системе, за тот же промежуток времени).