4.4. Точечные дефекты и пластическая деформация

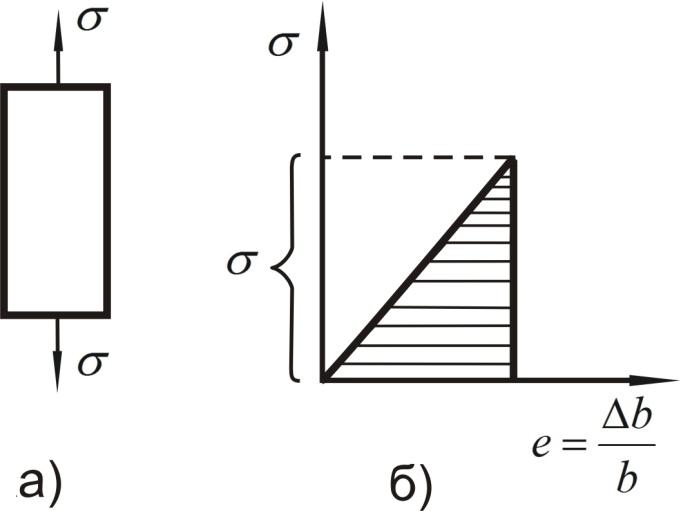
Допустим, что к металлическому бруску приложено растягивающее напряжение σ (рис.4.5, а). Согласно закону Гука в теле произойдет упругая деформация. Чтобы определить энергию (работу), затраченную на это, необходимо подсчитать площадь заштрихованного треугольника на рис.4.5, б. Она составит А=σ·∆b/2b, где b - параметр кристаллической решетки.

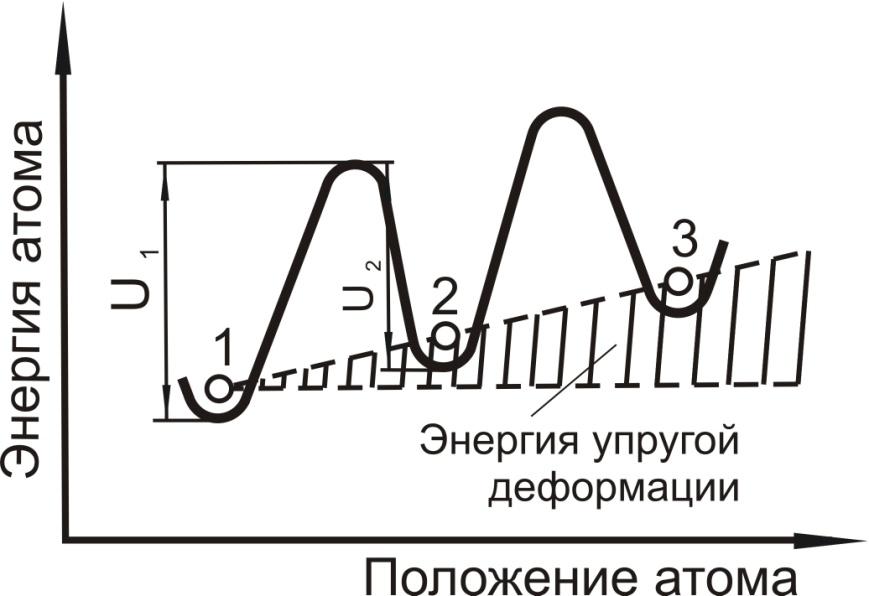
Рис.4.5. Графическое представление работы, затраченной на упругую деформацию.	Рис.4.6. Изменение энергетического состояния атома под действием упругой деформации.

В результате приложенной нагрузки произойдет искажение кристаллической решетки, т.е. нарушится правильное расположение атомов в пространстве. Атомы сместятся на величину ∆b (в среднем) от положения равновесия в направлении действия нагрузки. Рассмотрим, как изменится схема для энергии активации атома внутри кристаллической решетки, если учесть приложенное напряжение и полученную телом энергию упругой деформации (рис.4.6). Как видно из рисунка, упругая деформация изменяет обычную картину диффузионных процессов. Так, атому 1, например, труднее занять место атома 2 (надо затратить энергию U₁), чем атому 2 попасть в место 1 (надо затратить энергию U₂). Так как энергия активации U₂ < U₁, то перемещение атомов получит определенную направленность, т.e. приложив внешнюю нагрузку к металлу, можно создать преимущественную ориентацию диффузионных перемещений. В одном направлении перемещение атомов будет чаще, чем в других возможных направлениях. Такое явление получило название диффузионной пластичности, ибо при его наличии может происходить изменение формы тела, то есть его остаточная деформация.

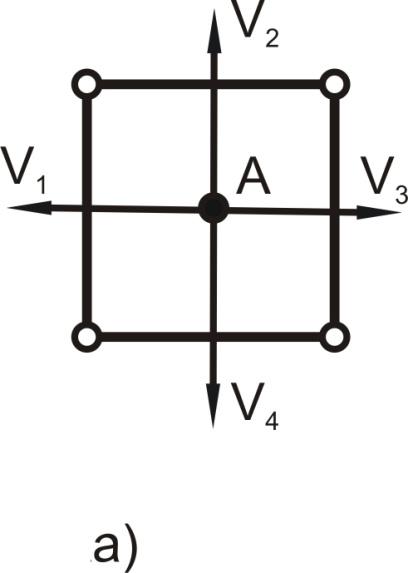
	На рис.4.7 показана схема, объясняющая диффузионную пластичность. Видно, что при отсутствии внешней нагрузки (рис.4.7, а) под воздействием температуры точечный дефект (межузельный атом А) может перемещаться равноценно в любом из четырех направлений (V1, V2, V3, V4), т.е. не будет преимущественного массопереноса.
Рис.4.7. Схема, объясняющая диффузионную пластичность.

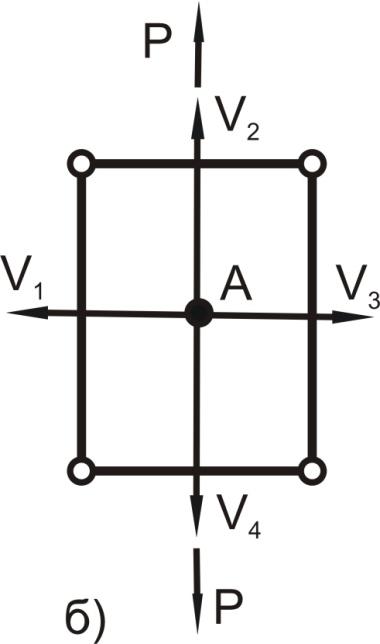
Приложение нагрузки Р (рис.4.7, б) упруго деформирует кристаллическую решетку, что создает преимущественную направленность (V₁, V₃) перемещения точечного дефекта.

Таким образом, приложенное напряжение к телу облегчает пере­мещение атома в одну сторону и затрудняет в другую. С учетом этого можно записать изменение энергии активации, как U ± γσ , где γ - некоторый структурно-чувствительный коэффициент, отражающий количество вещества, участвующего в рассматриваемом атомном механизме; σ- приложенное напряжение.

Уравнение Аррениуса в этом случае для "слабого" направления (V₁, V₃ ) примет вид:

n=N_o · exp (-(U-σ)/kT) (4.3)

Из уравнения видно, что внешние нагрузки способствуют процессу диффузионной пластичности и увеличению количества точечных дефектов, а это оказывает влияние на механические свойства материала. Как правило, с увеличением количества точечных дефектов прочность несколько возрастает, но не настолько сильно, чтобы объяснить наблюдаемые в опытах изменения прочности кристаллических тел.