3 Теоретическая и реальная прочность

кристаллов

3.1. Теоретическая прочность кристаллов

Основным механизмом пластической деформации является сдвиг одной части кристалла по отношению к другой под действием напря­жений.

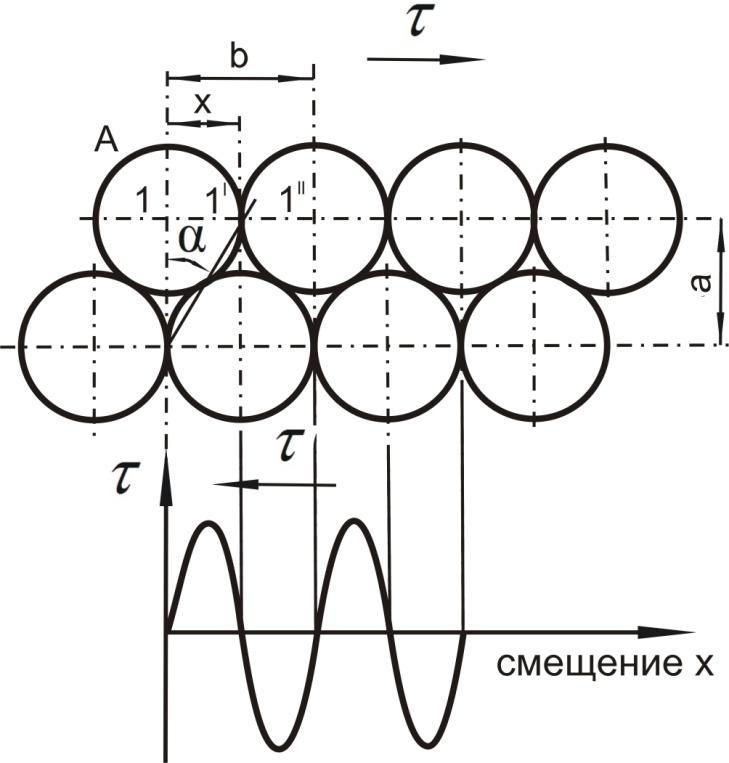
В 20-х годах советский физик Я.И.Френкель впервые надежно оценил предельную (теоретическую) прочность кристалла. Он предложил расчетную модель (рис.3.1) для оценки напряжения сдвига (τ), необходимого, чтобы все атомы части кристалла выше плоскости скольжения, под действием напряжения τ переместились относительно нижней плоскости одновременно на одно межатомное расстояние.

	Межплоскостное расстояние (расстояние между рядами) равно а, а расстояние между атомами в направлении скольжения равно б. Рассмотрим перемещение атома А. Под воздействием напряжения τ атом А и, соответственно, все атомы плоскости переместятся в положение 1. По мере перемещения атома А из положения 1 в положение 1// необходимо преодолевать возрастающие си-
Рис.3.1. Расчетная модель Я.И.Френкеля

лы межатомного отталкивания. Напряжение сдвига τ может быть описано периодической функцией х с периодом b в виде

τ = k sin(2πx/b) (3.1)

где k - постоянная величина. При малых смещениях х будет справедлив закон Гука τ = G·g=G·x/a (3.2)

где g =tgγ = x/a - деформация сдвига. Приравняв уравнения (1) и (2) для τ , получаем

k sin(2πx/b)= G·x/a (3.3)

При малых значениях х функция sin(2πx/b)= 2πx/b , тогда уравнение (3.3) запишется в виде k 2πx/b= G·x/a (3.4)

Из уравнения (3.4) определим значение k = G· b/2π a (3.5)

Подставляя значение k в уравнение (1), имеем

τ = (G· b/2π· a)·sin (2πx/b) (3.6)

Максимальное значение напряжения достигается при sin (2πx/b)= 1

τ = G· b/2π· a (3.7)

Можно принять, что а = b , тогда теоретическое критическое напряжение сдвига приближенно равно

τ = G/2π (3.8)

Сопоставление теоретических и фактических (реальных) значений напряжений сдвига показало значительное расхождение наблюдаемой прочности реальных кристаллов с теоретической (например, для железа τ_т = 11000 МПа, τ_ф = 290 МПа). Столь низкая прочность реальных кристаллов объясняется тем, что Френкель Я.И. рассматривал как бы идеальный кристалл. В реальных кристаллах существуют системы дефектов, которые резко снижают его прочность. Предсказанная Я.И. Френкелем прочность наблюдается только на идеально построенных в лабораторных условиях кристаллах.

3.2. Дефекты строения реальных кристаллических тел

Рассмотренное выше правильное расположение атомов в кристаллах - атомно-кристаллическая решетка со строго определенными параметрами и повторением совершенно одинаковых элементарных ячеек является идеальной схемой. В массивных кристаллах, в действительности, в отдельных местах практически всегда бывают отклонения от идеального построения атомов, которые называют дефектами кристалла.

Дефекты структуры металлических материалов классифицируют по геометрическому (размерному) признаку:

- точечные дефекты - нарушение периодичности расположения атомов в кристаллической решетке. Во всех трех измерениях они не превышают одного или нескольких межатомных расстояний;

- линейные дефекты (дислокации) - одномерные, т.е. протяженные в одном, измерении. Нарушения периодичности в одном измерении простираются на расстояния, сравнимые с размером кристалла, а в двух других измерениях не превышают нескольких параметров решетки;

- плоские или двумерные, дефекты простираются в двух измерениях на расстояния, сравнимые с размером кристалла, а в третьем - составляют несколько параметров решетки (мелкие трещины, границы зерен, поверхность кристалла, дефекты упаковки, малоугольные границы, например, границы между блоками мозаики);

- объемные, или трехмерные дефекты - это пустоты, поры, вклю­чения и т.п.