Кл 16. Типові задачі на застосування тягової характеристики

Задача 1. Автомобіль вагою  кН, який має коефіцієнт зчіпної ваги 0,75 і тягова характеристика якого за вільною силою тяги наведена на рис. 16.1, рухається без причепа по горизонтальній ділянці поля, коефіцієнт опору перекочування по якому дорівнює 0,1, а коефіцієнт зчеплення коліс з опорною поверхнею дорівнює 0,21.

На яких передачах може рухатись автомобіль у цих умовах?

Яку максимальну швидкість він може розвинути?

Розв’язок задачі. Тяговий баланс автомобіля за вільною силою тяги , записаний у інженерній формі для випадку ріномірного або прискореного руху машини має вигляд:

. (16.1)

Аналізуємо ліву частину тягового балансу (16.1). Вільна сила тяги, яка стоїть у лівій частині тягового балансу, має дві складові частини – значення, можливі за двигуном ( ) або значення, можливі за зчепленням ( ).

Вільна сила тяги за двигуном наведена на тяговій характеристиці суцільними лініями – рис. 16.1.

Вільна сила тяги за зчепленням наведена на рис.16.1 (пунктирними лініями) для кількох різних сил зчеплення коліс з опорною поверхнею . Для умов руху автомобіля, вказаних в умові задачі, сила зчеплення коліс з опорною поверхнею дорівнює:

25∙0,75∙0,21 = 3,94 кН ≈ 4 кН.

Лінія вільної сили тяги , можливої за зчепленням при такій силі зчеплення , на рис. 16.1 вже є. Інші лінії вільної сили тяги, наведені на рис. 16.1, нам вже не потрібні. Завдяки цьому ми можемо розглядати тягову характеристику у більш конкретному вигляді, який відображає саме ті умови, які вказано в умові задачі – рис. 16.2.

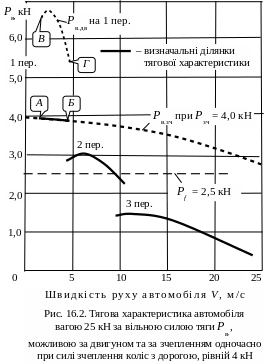
Під час руху на першій передачі визначальною є вільна сила тяги, можлива за зчепленням коліс – відрізок АБ лінії . Вільна сила тяги, можлива за двигуном (лінія ВГ) не є визначальною, бо вона не може бути реалізована за умовами зчеплення коліс з дорогою.

На другій і третій передачах визначальною є вільна сила тяги, можлива за двигуном, бо вона є меншою, ніж вільна сила тяги, можлива за зчепленням.

Позначаємо визначальні ділянки суцільними лініями – рис. 16.2.

Рис. 16.2 надає всі можливі числові значення вільної сили тяги автомобіля під час його руху в умовах, вказаних в умові задачі. Він визначає обидві складові частини лівої половини тягового балансу – сили .

Аналізуємо праву частину тягового балансу (16.1). З умови задачі випливає, що сила відсутня. Завдяки цьому баланс (16.1) спрощується до вигляду:

, (16.2)

права частина якого дорівнює:

=25∙0,1= 2,5 кН.

Таким чином, розв’язком задачі є нерівність

2,5 кН. (16.3)

Вона вказує, що для руху автомобіля потрібно, щоб його вільна сила тяги , можлива за двигуном та за зчепленням одночасно, була більшою, ніж сила опору рухові, рівна 2,5 кН.

На рис. 16.2 олівцем наносимо горизонтальну лінію 2,5 кН – див. пунктир на рис. 16.2.

Аналізуємо співвідношення між лівою і правою частинами тягового балансу. Для цього співставляємо лінію 2,5 кН з усіма іншими лініями тягової характеристиками, які описують вільну силу тяги машини , можливу за двигуном та за зчепленням.

Перша передача. Лінія АБ, яка визначає вільну силу тяги , можливу на 1 передачі, проходить вище лінії 2,5 кН. Це означає, що умова (16.3) виконується, тобто автомобіль може рухатись на першій передачі. Якщо автомобіль буде рухатись рівномірно, то його вільна сила тяги, можлива за двигуном, буде дорівнювати 2,5 кН (згідно з третім законом Ньютона). При цьому існуватиме запас сили зчеплення, рівний приблизно 4 – 2,5 = 1,5 кН. Тобто автомобіль рухатиметься без буксування коліс.

Якщо ж водій буде розганяти автомобіль, натиснувши на педаль акселератора, то можлива за двигуном вільна сила тяги буде перевищувати 2,5 кН. Але при досягненні значення 4 кН, максимально можливого за зчепленням, колеса забуксують і сила тяги більше не зростатиме. Тобто максимально можлива вільна сила тяги, яку може розвивати автомобіль на 1 передачі, дорівнює приблизно 4 кН і інтенсивний розгін автомобіля при цьому відбуватиметься з буксуванням коліс.

Друга передача. Під час руху на 2 передачі визначальною є можлива за двигуном вільна сила тяги і порівнювати з лінією сили опору рухові 2,5 кН потрібно саме її. Лінія перетинається з лінією сили опору рухові  = 2,5 кН при швидкості приблизно 9 м/с. Це означає, що на другій передачі вільна сила тяги, можлива за двигуном, перевищує силу опору рухові лише на швидкостях до 9 м/с. Тобто автомобіль може рухатись на цій передачі, але з швидкістю не більшою 9 м/с.

Під час рівномірного руху автомобіля на 2 передачі його вільна сила тяги, можлива за двигуном, буде дорівнювати 2,5 кН (згідно з третім законом Ньютона). При цьому існуватиме запас сили тяги за двигуном, максимальне значення якого дорівнює 3 – 2,5 = 0,5 кН.

Якщо ж водій максимально натисне на педаль акселератора, то можлива за двигуном вільна сила тяги буде зростати, але не зможе перевищити значення, рівне приблизно 3 кН. Воно істотно менше можливого за зчепленням, рівного приблизно 4 кН. Завдяки цьому розгін автомобіля відбуватиметься без буксування коліс.

Третя передача. Під час руху на 3 передачі визначальною є можлива за двигуном вільна сила тяги і порівнювати з лінією сили опору рухові 2,5 кН потрібно саме її.

Визначальна лінія приходить нижче лінії сили опору рухові  = 2,5 кН. Це означає, що на третій передачі вільна сила тяги менша за силу опору рухові. Тобто автомобіль не зможе рухатись на цій передачі.

Задача 2. Автомобіль вагою  кН, який має коефіцієнт зчіпної ваги 0,75 і тягова характеристика якого за вільною силою тяги наведена на рис. 16.2, рухається без причепа на підйомі грунтової дороги, коефіцієнт опору перекочування по якій дорівнює 0,05, кут підйому дороги рад, а коефіцієнт зчеплення коліс з дорогою дорівнює 0,21.

На якій передачі може рухатись автомобіль на даному підйомі?

З якою максимальною швидкістю автомобіль може рухатись на даному підйомі?

Розв’язок. Користуємось тим же тяговим балансом, що і у задачі 3:

.

Всі числові значення лівої частини балансу наведені у тяговій характеристиці автомобіля, рис. 16.2.

Права частина тягового балансу дорівнює:

=25∙(0,05+0,05) = 2,5 кН.

На рис. 16.2 олівцем наносимо горизонтальну лінію 2,5 кН – див. пунктир 2,5 кН на вказаному рисунку.

Таким чином, розв’язком задачі є нерівність 2,5 кН, тобто розв’язок даної задачі не відрізняється від розв’язку задачі 1.

Задача 3. Умова – та ж, що і у задачі 4, але потрібно визначити наступне.

1. Який максимально можливий підйом на даній дорозі може подолати автомобіль, якщо буде рухатись рівномірно?

2. Яке максимально можливе прискорення може мати автомобіль на 5 % підйомі , якщо коефіцієнт приведення, який враховує наявність обертових мас, дорівнює 1,5?

Розв’язок п. 1. Рис. 16.2 свідчить, що на першій передачі визначальною є вільна сила тяги , можлива за зчепленням і рівна приблизно 4 кН (див. відрізок АБ).

Під час рівномірного руху на підйом вона витрачається на подолання сил опорів перекочуванню і підйому (користуємось балансом вільної сили тяги, наведеним у задачі 2, але із знаком «=» замість знака « »):

.

Звідси підйом, який може подолати автомобіль на першій передачі, дорівнює:

.

Розв’язок п. 2. У процесі розгону, який здійснюється на підйомі, визначальна сила тяги , яка дорівнює приблизно 4 кН, витрачається на подолання сил опору перекочуванню, підйому і інерції, внаслідок чого тяговий баланс, записаний у науковій формі, має вигляд:

,

де – поступальне перевантаження – безрозмірністна величина, яка вказує, у скільки разів прискорення більше за прискорення земного тяжіння .

Розв’язавши останній вираз відносно величини , знаходимо:

.

Таким чином, автомобіль може мати поступальне прискорення, рівне 0,040·g, тобто 0,39 м/с².