Задача 7

Имеются следующие условные данные по трем группам рабочих с разным стажем работы:

Стаж работы (лет)	Число рабочих пi	Средняя дневная зарплата, руб.	Среднее квадратическое отклонение зарплаты, руб.
До З 3-10 Более 10	10 15 25	500 600 700	12 10 20

Рассчитать: а) среднюю дневную зарплату для всей совокупности рабо­чих; б) общую дисперсию и среднее квадратическое отклонение зар­платы.

Решение: Общая средняя

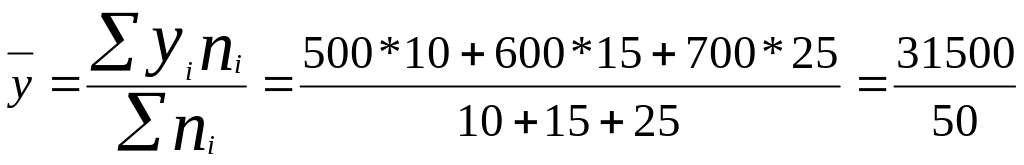= 630 (руб.).

Общая дисперсия находится по правилу сложения дисперсий:

.

Находим среднюю из групповых дисперсий:

.

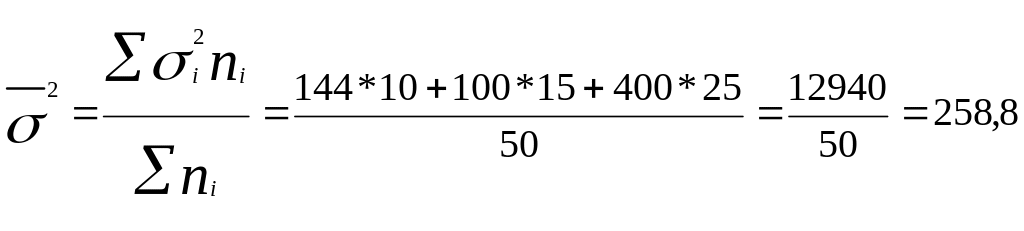Межгрупповая дисперсия

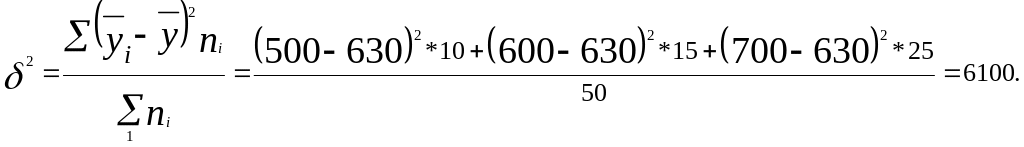Общая дисперсия зарплаты

= 258,8 + 6100 = 6358,8.

Отсюда среднее квадратическое отклонение зарплаты во всей совокупности рабочих

79,7 (руб.).

Примечание. Соотношение моды, медианы и средней арифметической указывает на характер распределения признака в совокупности, позволяет оценить его асимметрию. Если , то имеет место правосторонняя асимметрия, при следует сделать вывод о левосторонней асимметрии ряда.

Средняя арифметическая часто используется как показатель центра распределения, положительные и отрицательные отклонения от которого индивидуальных значений признака в сумме взаимно погашаются.

Медиана отражает значение признака, сумма отклонений от которого, является наименьшей величиной.

Мода является величиной, вокруг которой группируется наибольшее количество единиц совокупности. При нормальном распределении все эти три показателя имеют одинаковую величину.

Установив значения характеристик центра распределения ( ), возникает вопрос, в какой мере индивидуальные значения признака отличаются между собой и центральных характеристик от средней. Для этого рассчитываются показатели вариации.

Чем меньше вариация, тем более однородна совокупность и более надежна (типична) средняя величина.

Среднее квадратическое отклонение также, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения.

Среднее линейное отклонение обладает большим преимуществом перед размахом вариации в отношении полноты характеристики колеблемости признака. Однако при этом в некотором смысле нарушается элементарное правило математики, так как отклонения от среднего значения признака складываются без учета знаков.

Среднее квадратическое отклонение измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака (рублях, тоннах, процентах и т. д.). Оно является абсолютной мерой вариации.

Чем больше коэффициент вариации, тем менее однородная совокупность и тем менее типична средняя для данной совокупности. Установлено, в соответствии со свойствами нормального распределения, что совокупность количественно однородна, если коэффициент вариации не превышает 33%.