Задача 6

Имеются следующие данные о распределении семей их 3-х человек по размеру годового денежного дохода. (графы 1,2, 3 табл., ниже см.).

Определить:

1) годовой доход семей с помощью средней арифметической, моды и медианы;

2) среднее квадратическое отклонение годового дохода и ко­эффициент вариации;

3) децильный коэффициент дифференциации доходов;

4) степень концентрации (неравномерности) доходов у отдель­ных семей (коэффициент Джини).

Решение. Необходимые для расчета суммы показаны в таблице.

1. а) Средний годовой доход

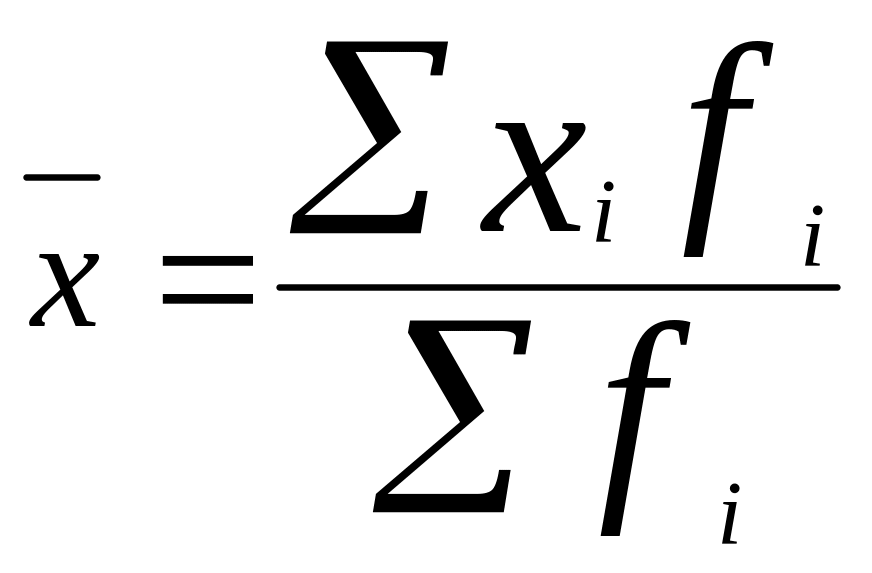= 900,75 (тыс. руб.).

(В качестве весов можно принимать и w_i — относительный по­казатель численности семей в % к итогу. Результат будет тот же.).

Таблица

Годовой доход семьи, тыс. руб.	Численность семей		Середина интервала xi	Суммарный доход по группам xifi	Накоп- ленные частости (доли семей в %) Si=pi	xi2fi
	тыс., fi	%
		к итогу,
		wi
1	2	3	4	5	6	7
До 400 400-600 600-800 800-1000 1000-1200 1200-1600 1600-2000 Свыше 2000	25,8 28,7 24,7 19,2 13,8 16,6 8,4 10,3	17,5 19,5 16,7 13,0 9,4 11,2 5,7 7,0	300 500 700 900 1100 1400 1800. 2200	7740 14 350 17 290 17 280 15 180 23 240 15 120 22 660	17,5 37,0 53,7 66,7 76,1 87,3 93,0	2 322 000 7 175 000 12 103 000 15 552 000 16 698 000 32 536 000 27 216 000 49 852 000
					100
Итого	147,5	100,0	—	132 860	—	163 454 000

б) Мода (наиболее часто встречающийся размер годового дохо­да) находится в интервале 400—600. Определим ее как

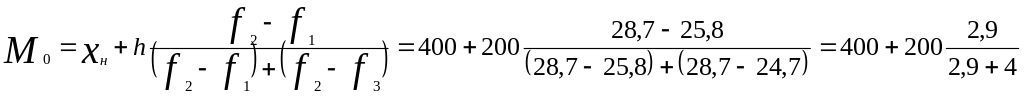= =484 (тыс. руб.),

где х_н — нижняя граница модального интервала.

в) Медиану удобнее находить по данным распределения в %, т.е. по w_i.Тогда порядковый номер медианы равен 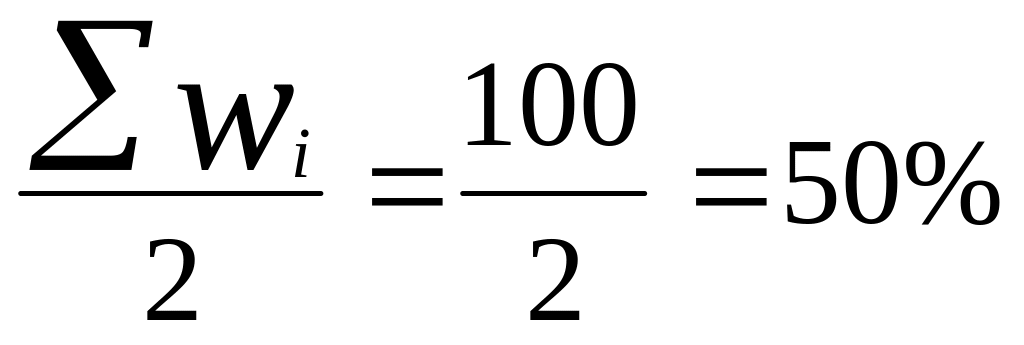. По накопленным частостям определяем, что медиана (50-й процент) находится в интервале 600—800.

Отсюда

Ме= (тыс. руб.),

т.е. в июле 1997 г. половина семей имела годовой денежный доход ниже 755,7 тыс. руб., а половина — выше 755,7 тыс.

2. а) Среднее квадратическое отклонение найдем по формуле

(тыс. руб.).

(Можно было использовать и формулу )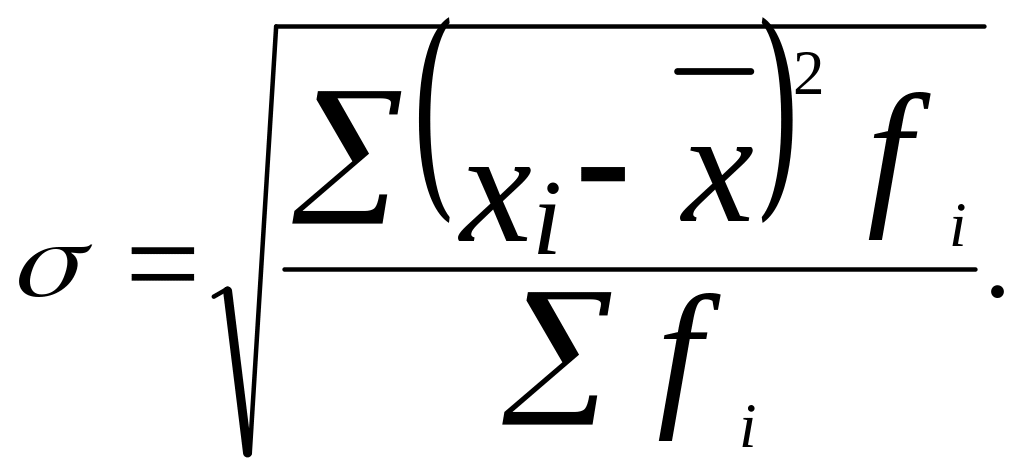

б) Коэффициент вариации

= 60%.

Такая вариация весьма значительна, т.е. годовые доходы семей далеко не однородны по размеру.

3. Для оценки степени дифференциации доходов по накоплен­ным частостям (графа 6) определяем, что первая дециль (D₁) нахо­дится в первом интервале (200—400), а девятая дециль (D₉) — в пред­последнем интервале (1600—2000):

a) 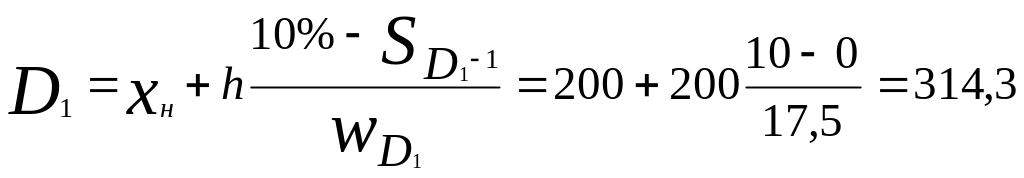(тыс.руб.).

D₁ — это максимальный размер годового дохода у десяти процен­тов семей с наименьшими доходами.

Учитывая, что частость первого интервала (17,5%) больше 10% (порядкового номера D₁), расчет D₁ удобнее вести от значения верх­ней границы интервала, вычитая из него величину интервала, при­ходящуюся на излишние 7,5% единиц, т.е.

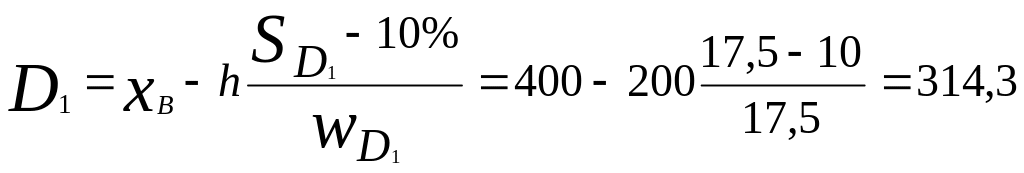(тыс.руб.)

б) 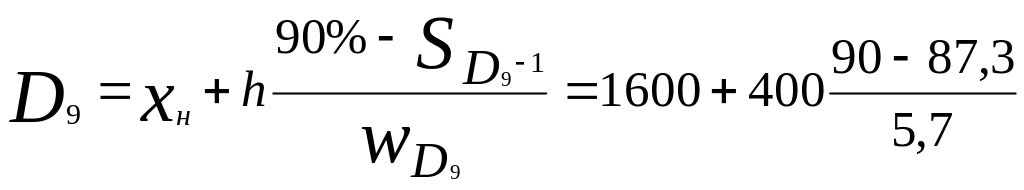= 1600 + 189,5 = 1789,5 (тыс. руб.).

D₉ - это минимальный размер годового дохода у десяти процен­тов семей с наиболее высокими доходами;

в) децильный коэффициент дифференциации {ДКД) доходов

ДКД =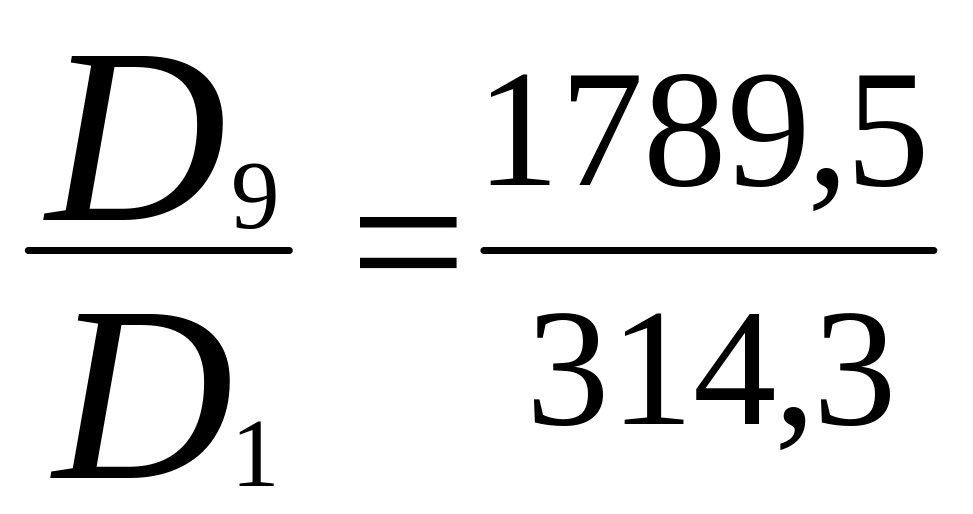 = 5,7 (раза).

Примечание. Поскольку в первом интервале не указана нижняя гра­ница, а последующий интервал равен 200 (400—600), то мы вправе и в первом интервале принимать такую же величину, т.е. (200—400).

4. Для расчета коэффициента Джини, G, сначала определяем долю (в %) суммарного дохода по каждой группе как (x_if_i: Σ x_if_i )* 100% (графа 8 в продолжении табл. 1), а затем в графе 9 находим кумулятивные (накопленные) итоги суммарного дохода в % (q_i).

Продолжение табл. 1

Суммарный доход по группам, % к итогу (xifi: Σ xifi )* 100%	Накопленные итоги суммарного дохода, % qi
8	9
5,8 10,8 13,0 13,0 11,4 17,5 11,4 17,1	5,8 16,6 29,6 42,6 54,0 71,5 82,9 100,0
100,0	—

По данным граф 6 и 9,

= [(17,5*16,6 + 37*29,6 + 53,7*42,6 + 66,7*54 + 76,1*71,5 + 87,3*82,9 + 93*100) - (37,0*5,8 + 53,7*16,6 + 66,7*29,6 + 76,1* *42,6 + 87,3*54 + 93*71,5 + 100*82,9)] : 10 000 = (29253,44 - 25975,9) : 10 000 = 0,327 0,33.

По G = 0,33 делаем вывод, что степень концентрации суммар­ных годовых денежных доходов у семей с более высокими доходами сред­няя, не очень высокая.