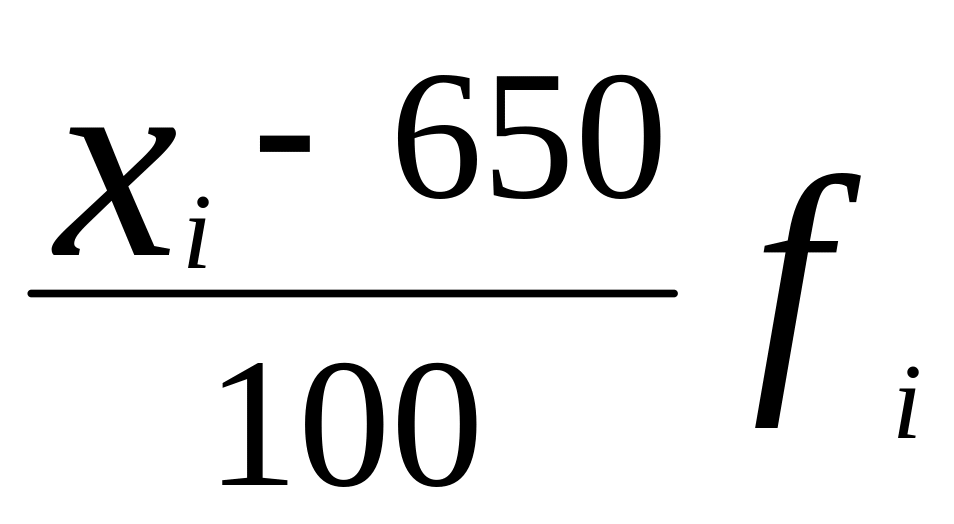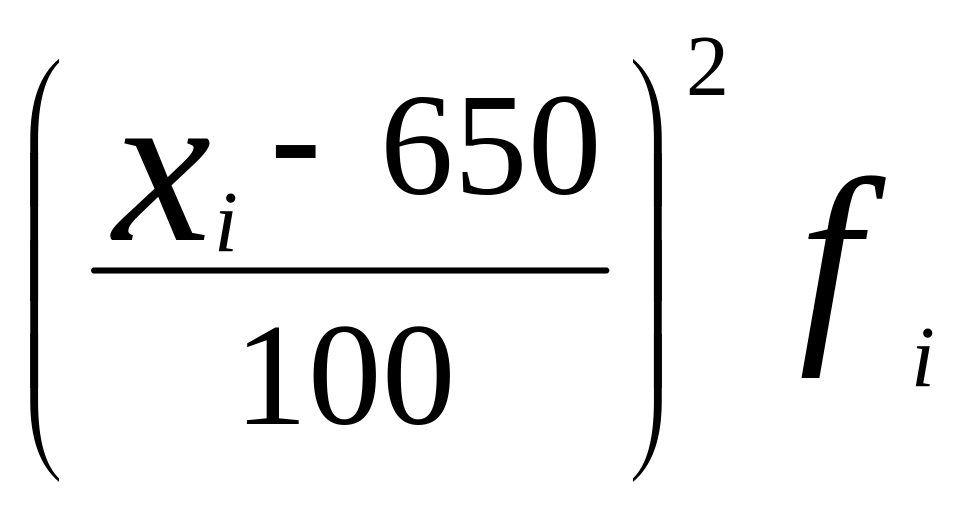Задача 3

Воспользовавшись исходными данными задачи

Имеется следующее распределение 60 рабочих по тарифному разряду:

Тарифный разряд х.	2	3	4	5	6
Число рабочих f.	8	16	17	12	7

где =3,9, рассчитаем основные показатели вариации. Расчет оформим в сле­дующей таблице:

xi	fi
2 3 4 5 6	8 16 17 12 7	1,9 0,9 0,1 1,1 2,1	15,2 14,4 1,7 13,2 14,7	28,88 12,96 0,17 14,52 30,87
Σ	60	—	59,2	87,40

А. Среднее линейное отклонение:

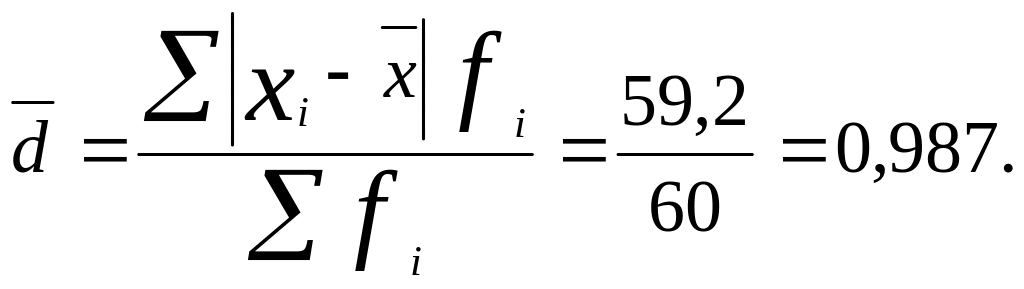
Б. Дисперсия:

В. Среднее квадратическое отклонение:

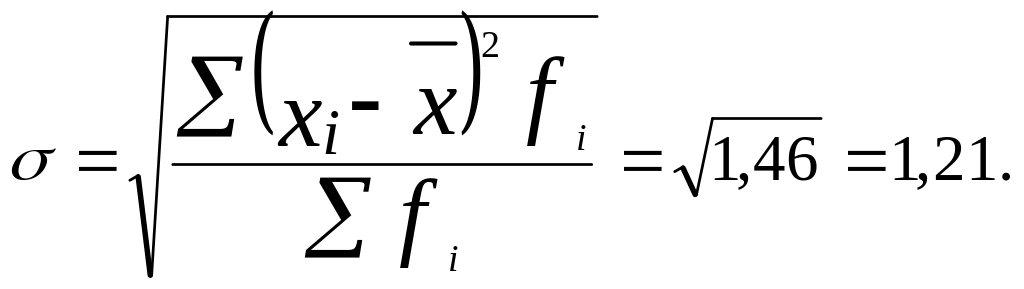
Г. Коэффициент вариации:

Задача 4

Воспользовавшись исходными данными задачи

Дневная заработная плата, руб.	Число рабочих fi	Середина интер- вала Xi	Xifi
1	2	3	4
400-500	10	450	4500
500-600	20	550	11 000
600-700	48	650	31 200
700-800	60	750	45 000
800-900	42	850	35 700
900-1000	20	950	19 000
Итого	200	—	146 400

Рассчитаем среднюю арифметическую, дисперсию и коэффициент вариации, предварительно уменьшив до предела варианты (т.е. способом расче­та от условного нуля):

Середина интервала х.i	Частоты fi
450	10	-2	-20	40
550	20	-1	-20	20
650	48	0	0	0
750	60	1	60	60
850	42	2	84	168
950	20	3	60	180
Σ	200	—	164	468

1. Средняя арифметическая

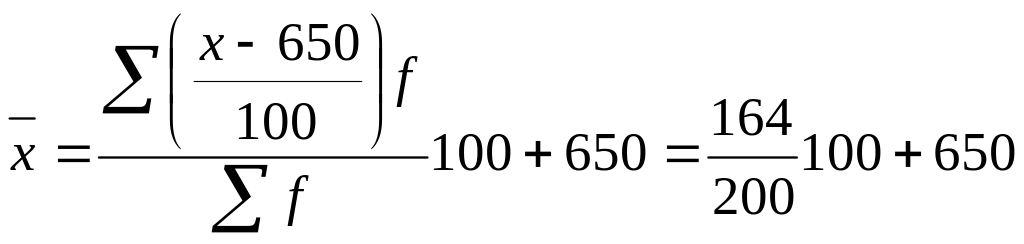= 732 (руб.).

2. Рассчитаем дисперсию. Сначала найдем средний квадрат от­клонений от произвольного числа — в нашем примере от 650, а за­тем скорректируем его на квадрат разности между средней арифме­тической и этим произвольным числом, т.е. применим формулу

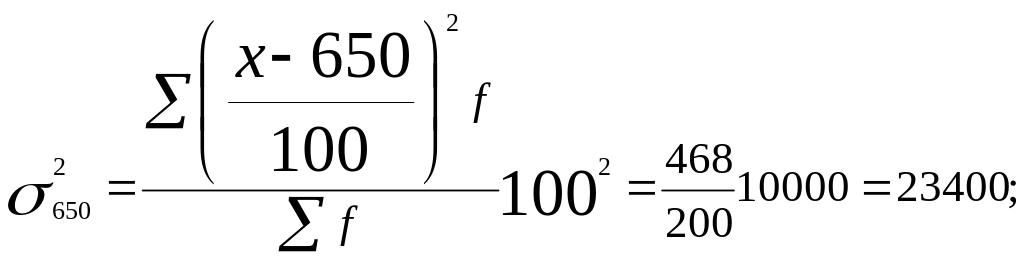
3. Отсюда среднее квадратическое отклонение

.

4. Коэффициент вариации

V= 100% = 17,6%.

Задача 5

Пусть имеются следующие данные о результатах экзаменацион­ной сессии на I и II курсах одного из вузов: на I курсе 85% студентов сдали сессию без двоек, а на II курсе - 90%. Определить дисперсию доли студентов, успешно сдавших сессию (или, что то же самое, доли студентов, получивших двойки на сессии).

Так как p₁= 0,85 и q₁ = 0,15, а р₂ = 0,9 и q₂ = 0,1, то:

на I курсе σ²₁=p₁q₁ = 0,85 • 0,15 = 0,1275 => σ₁ = 0,35;

на II курсе σ²₂ = р₂ q₂ = 0,9 • 0,1 = 0,09 => σ₂ = 0,3.

Следовательно, на II курсе дисперсия и среднее квадратическое отклонение доли студентов, успешно сдавших сессию, меньше, чем на I курсе.