13

Практика №2

Мода и медиана. Меры вариации.

Задачи для самостоятельного решения

(см. методические рекомендации стр.4)

Задача 1

Имеется следующее распределе­ние безработных по возрастным группам:

Возрастные группы, лет	Численность безра- ботных, % к итогу
16-19	10,2
20-24	17,9
25-29	12,7
30-49	48,8
50-54	4,0
55-59	4,5
60-72	1,9
Всего	100,0

По данным распределения определить:

1) средний (арифметический) возраст безработных;

2) среднее квадратическое отклонение;

3) коэффициент вариации.

Ответ: 1) = 34,3 года;

2) σ = 11,5 года; 3) V= 33,5%.

Задача 2

Имеются следующие данные за 2005 и 2006 гг. об урожай­ности, посевных площадях и валовом сборе пшеницы (озимой и яровой).

Культура	2005		2006
	Урожайность, ц/га	Посевная площадь, млн.га	Урожайность, ц/га	Валовой сбор,млн.ц
Пшеница озимая Пшеница яровая	16,9 10,3	8,2 15,8	17,9 11,0	167 182

Определить среднюю урожайность пшеницы: а) в 2005 г. и б) в 2006 г.

О т в е т: а) 12,56 ц/га; б) 13,48 ц/га.

Задача 3

По данным таблицы

Распределение численности безработных по возрастным группам

Возрастная	Численность безработных, % к итогу
группа	мужчины	женщины
16 - 19 лет	7,7	11,2
20 - 24	17,0	18,5
25 - 29	11,9	11,7
30 - 49	50,9	49,5
50 - 54	4,2	4,0
55-59	5,7	3,8
60-72	2,6	1,3
Итого	100,0	100,0

определить средний возраст безработных: а) мужчин; б) женщин.

Ответ: а) 35,5 года; б) 33,8 года.

Задача 4 (похожая задача будет в контрольной работе)

Имеются следующие данные о распределении семей области по уровню среднегодового дохода.

Среднегодового дохода семьи, тыс. руб.	Численность
	семей,
	% к итогу
До 200 200-400 400-600 600-800 800-1000 Свыше 1000	15,3
	50,6
	23,5
	7,3
	2,2
	1,1

Определить в данном распределении:

1) среднегодовой доход семей по области в целом;

2) моду;

3) медиану;

4) среднее квадратическое откло­нение доходов; дисперсию, коэффициент вариации.

5) дециальный коэффициент дифференциации (ДКД) доходов;

6) коэффициент Джини (G).

Ответ: 1) = 367,6 тыс. руб.; 2) Мо = 313,1 тыс. руб.;

3). Me = 337,2 тыс. руб.; 4)σ = 193,8 тыс. руб.;

5) ДКД = 4,7 раза; 6) G= 0,76.

Задача 5

По переписи населения 1926 г. в России доля грамотных среди женщин составляла 46%, а среди мужчин 77%. Определить общий (средний) процент грамотности всего населения и дисперсию этого показателя, если женщины составляли 53% в общей численности населения.

О т в е т: 1) = 60,57% (0,6057); 2)σ² = = 0,2388.

Задача 6

В коллективных хозяйствах района средняя урожайность зерновых составила 19 ц/га при среднем квадратическом отклонении 3 ц/га, а в фермерских хозяйствах — соответственно 26 ц/га и 4 ц/га.

Определить:

1) среднюю урожайность зерновых по району, если известно, что посевная площадь под зерновыми в коллективных хо­зяйствах в 9 раз превышает площадь фермерских хозяйств;

2) общую дисперсию и среднее квадратическое отклонение уро­жайности зерновых в районе (по правилу сложения диспер­сии).

О т в е т: 1) = 19,7 ц/га;

2) σ² = ² + δ² = 8,5 + 4,41 = 12,91, σ = 3,6 ц/га.

Задача 7

Для изучения уровня заработной платы рабочих на предприя­тии выборочно обследовано 500 мужчин и 300 женщин. Результаты исследования показали, что у мужчин средняя заработная плата со­ставила 1200 руб. при среднем квадратическом отклонении 200 руб., а у женщин — соответственно 800 руб. и 150 руб.

Определить:

1) общую среднюю заработную плату рабочих на заводе;

2) среднюю из групповых дисперсий;

3) межгрупповую дисперсию;

4) общую дисперсию зарплаты;

5) коэффициент вариации зарплаты на предприятии.

Ответ: 1) = 1050 руб.; 2) = 33 437,5; 3) δ² = 37 500;

4) σ² = 70 937,5; 5) V= 25,4%.

Методические рекомендации для студентов

Задача 1

Определить моду по данным:

Дневная заработная плата, руб.	Число рабочих fi	Середина интер- вала Xi	Xifi
1	2	3	4
400-500	10	450	4500
500-600	20	550	11 000
600-700	48	650	31 200
700-800	60	750	45 000
800-900	42	850	35 700
900-1000	20	950	19 000
Итого	200	—	146 400

Для интервального ряда с равными интервалами мода рассчи­тывается по формуле

,

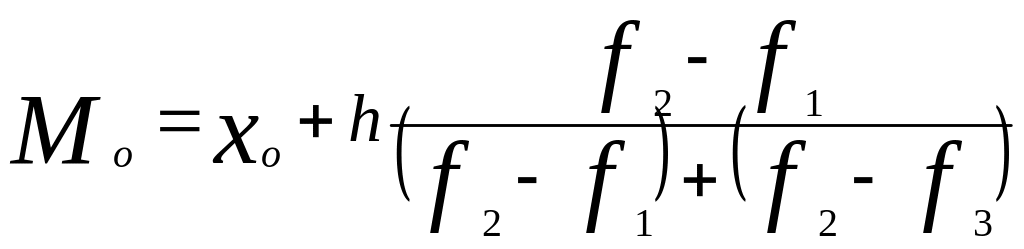где x₀ - начальная (нижняя) граница модального интервала;

h - величина интервала;

f₂ - частота модального интервала;

f₁ - частота интервала, предшествующего модальному;

f₃ - частота интервала, следующего за модальным.

В условии задачи наибольшую частоту (60) имеет интервал (700—800). Отсюда

Мо =700 + 100 (руб.)

т.е. наиболее часто встречается дневная заработная плата в размере 731,6 руб.

В ряду с неравными интервалами мода определяется в интерва­ле, имеющем наибольшую плотность распределения, и в формуле вместо f₁, f₂, f₃, принимаются соответствующие плотности распреде­ления.