Задача 10

Проверить прочность балки, нагруженной поперечными нагрузками в двух плоскостях, совпадающих с главными центральными плоскостями поперечных сечений ( задача 6, гл. 2 ), если l = 0,8 м, q = 0,8 кН/м, [  ] = 160 МПа.

Поперечное сечение балки состоит из швеллера № 14 и уголка № 8, гeoметрическиe характеристики которого найдены и составляют I _x = 707 см ⁴, I _y = 146 см ⁴.

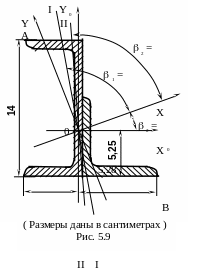
Как следует из рис. 2.17 в, г, е, ж, в поперечных сечениях балки воз-никают ( такое нагружение называется косым изгибом ). Нормальные напряжения определяются по формуле

Касательными напряжениями, со-ответствующими поперечным силам, обычно в расчетах на прочность пренебрегают ( как и при плоском поперечном изгибе ) ввиду их малости в сравнении с наиболь-шими нормальными напряжениями.

В рассматриваемой задаче опасными могут быть два сечения:

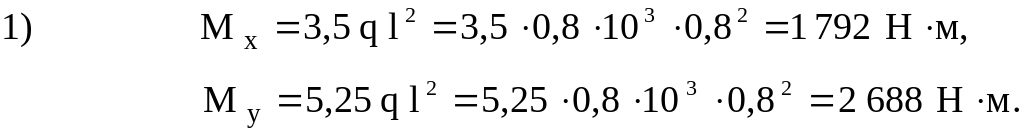
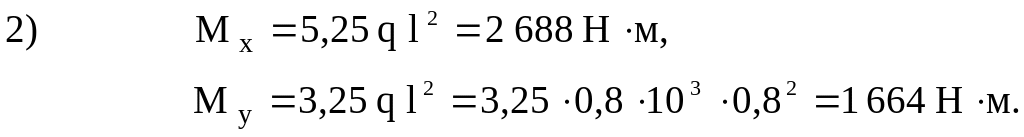
Наибольшие напряжения будут в точках, наиболее удаленных от нулевой линии.

Уравнение нулевой линии

или

где – угловой коэффициент.

Здесь – угол, образуемый нулевой линией с осью Х.

Проверка прочности.

1-е сечение

Нулевая линия 1 – 1 проведена на рис. 5.9. Наиболее удалена от нулевой линии точка В, ее координаты: тогда

Таким образом, условие прочности выполняется.

2-е сечение

Нулевая линия II – II показана на рис. 5.9. В этом сечении наиболее опасной точкой также является точка В, в которой

И в этой опасной точке 2-го сечения  _max < [  ]. По результатам проверки прочности делаем вывод, что прочность балки обеспечена.

Задача 11

Для заданного стержня с указанным поперечным сечением вычислить максимальные нормальные и касательные напряжения , построить графики их распределения по высоте сечения при следующих данных :

q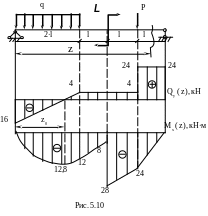 = 10 кН∙м , P = 20 кН , L = 20 кН∙м ,

l = 1 м .

Поперечное сечение – двутавр № 20 . Выписываем характеристики дву-тавра № 20 по ГОСТ 8239 – 72 .

I_x = 1840 см ⁴ , W_x = 184 см ³ ‚

d = 0,52 см , t = 0,84 см ,

h = 200 мм , b = 100 мм ,

S_x = 104 см ³.

Вычислим интегральные харак-теристики напряжений

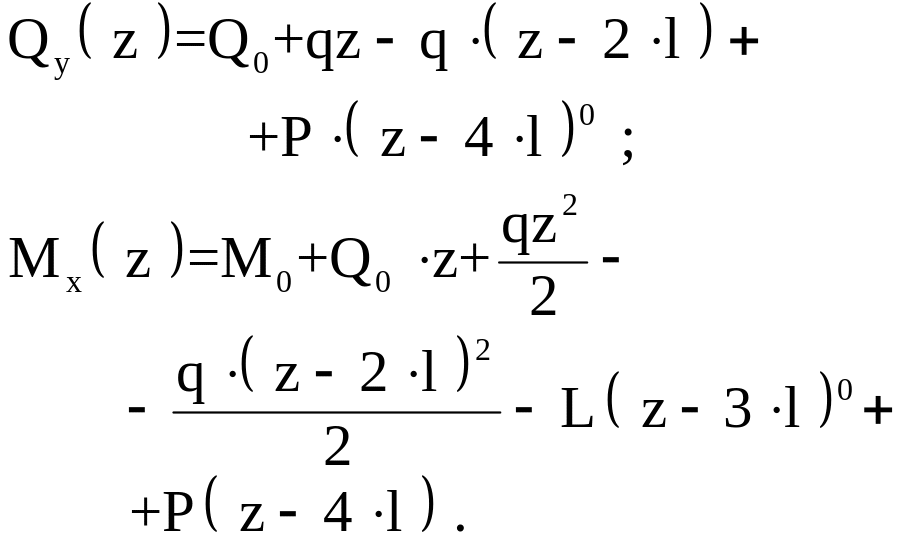
Из граничных условий на концах стержня

Так как Q_y на первом участке меняет знак , то на графике M_x будет экстремум.

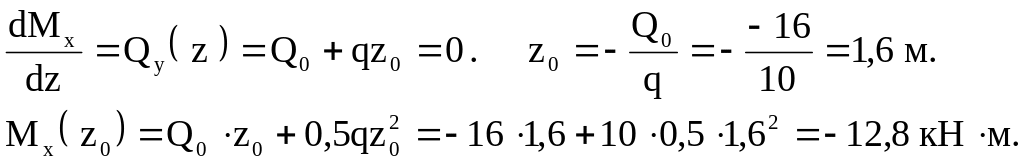
По этим значениям построим графики Q_y и M_x ( рис. 5.10 ) . Опасным является сечение , где приложен сосредоточенный момент L .

|M_x|_max =28 кН∙н , Q_y=4 кН .

Максимальные напряжения

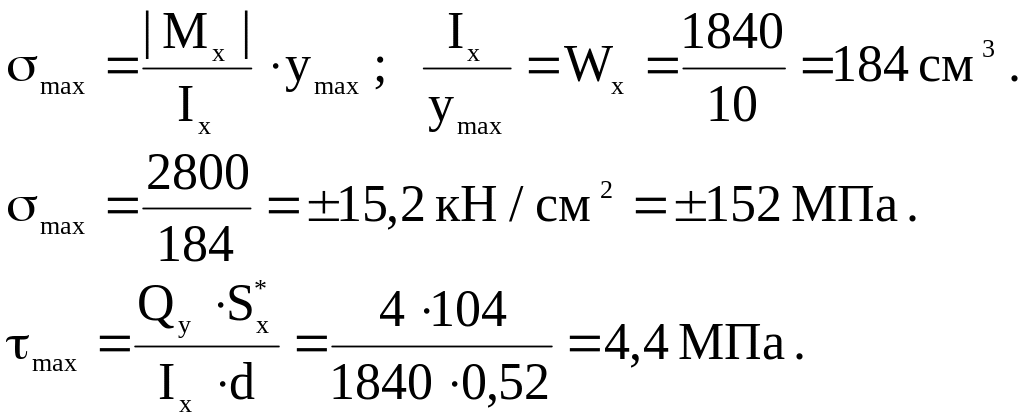
Нормальные напряжения при переходе к полкам будут равны

Касательные напряжения при переходе от стенки к полке будут равны

Г рафик распределе-ния нормальных и каса-тельных напряжений по высоте сечения показан на рис. 5.11.

Задача 12

В опасном сечении стержня вычислить эквивалентные напряжения по третьей теории прочности при следующих исходных данных :

P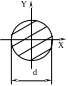 = 20 кН , q = 12 кН / м , L = 16 кН∙м , l = 0,6 м , d = 20 см .

1. Запишем выражения интегральных характеристик напряжений :

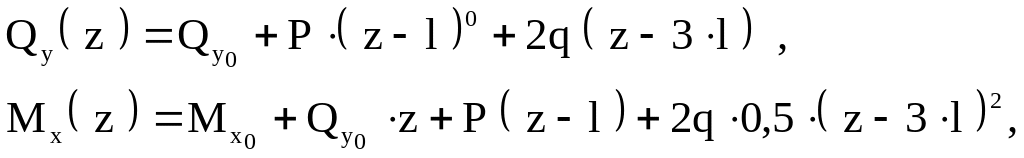
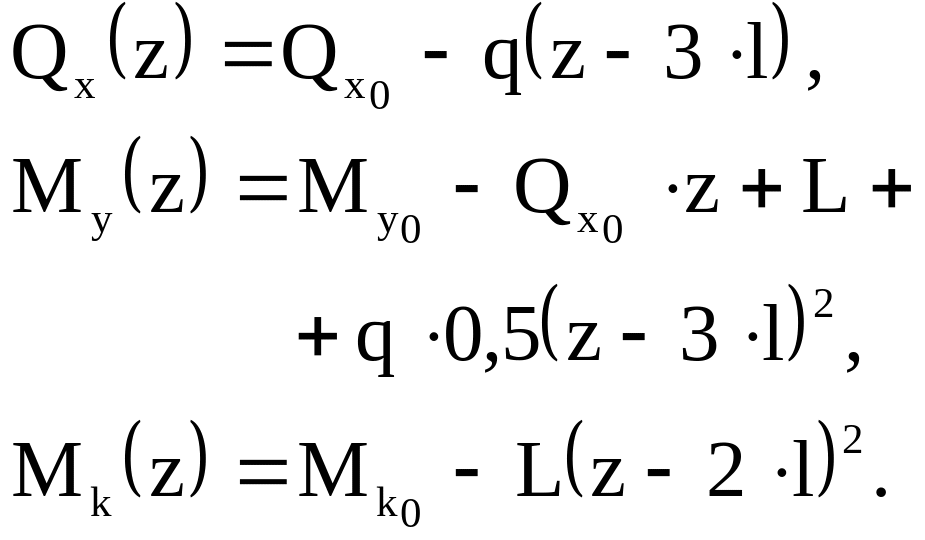
Из граничных условий на свободном конце стержня определим начальные значения :

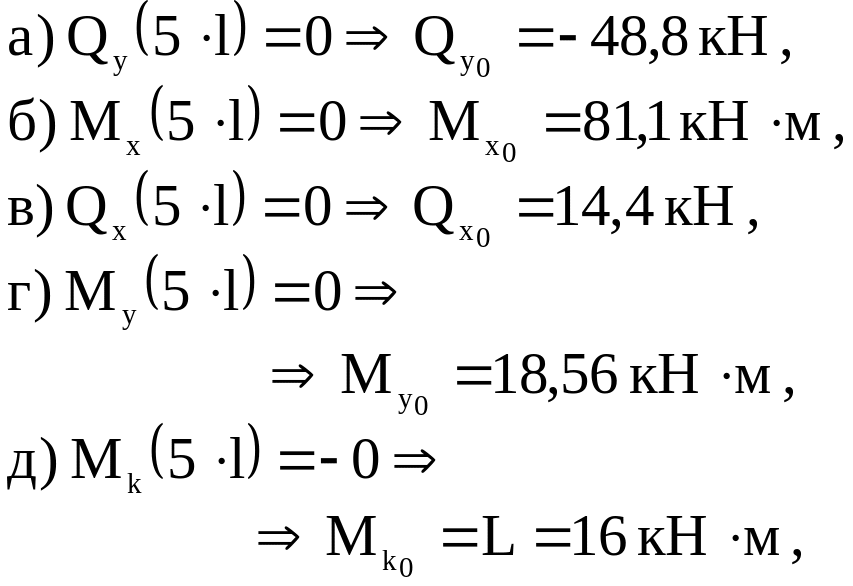Вычислим значения интеграль-ных характеристик в характер-ных точках стержня :

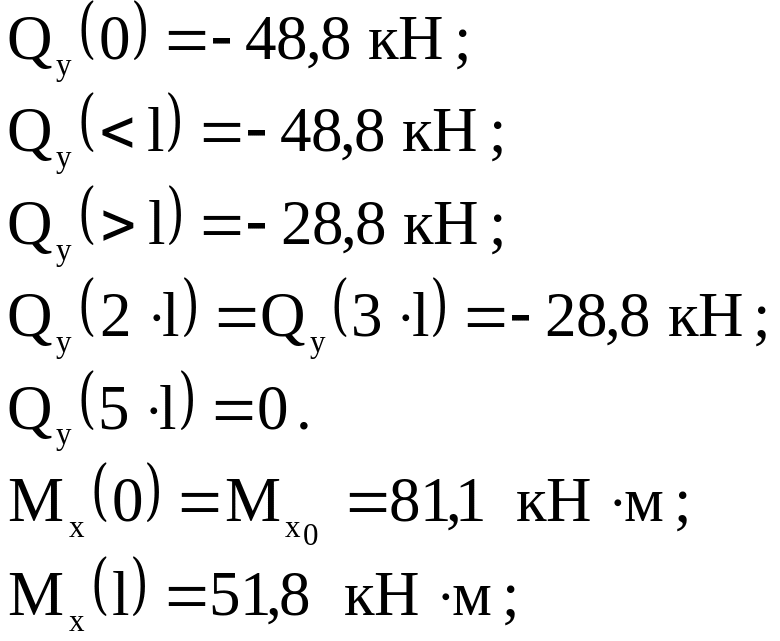
По этим значениям строим графики Q_y(z), M_x(z), Q_x(z), M_y(z), M_k(z) ( рис. 5.12 ) . Вычислим эквивалентные напряжения по третьей теории прочности в двух наиболее опасных сечениях ( I и II ) стержня:

Таким образом‚ наиболее опасным является сечение в заделке.

Задача 13

Вал круглого сечения длиной l = 2 м с жёсткозаделанными концами посередине пролёта подвергается действию сосредоточенной силы P = 10 кН с эксцентриситетом h = 10 см ( рис. 5.13 ) . Вычислить диаметр вала d по третьей теории прочности при условии , что допускаемое напряжение [σ] = 200 МПа .

П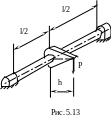 од действием силы Р вал изгибается и скручи-вается . При этом возникают нормальные σ_z и каса-тельные τ_k напряжения в сечении стержня:

Тогда условие прочности ( 5.12 ) запишем как

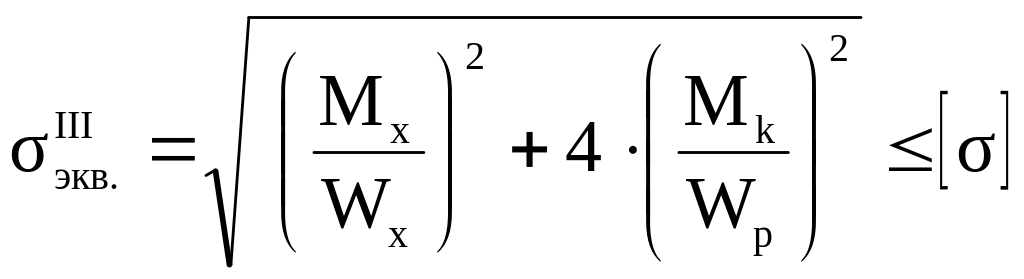. ( 5.16 )

Учитывая , что W_x 0,1d³ и W_p0,2d³‚ найдем из ( 5.16 ) диаметр вала

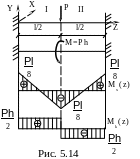( 5.17 )

По принципу независимости действия сил стержень изгибается силой Р и скручивается моментом M = P·h ( рис. 5.14 ) . Для нахождения уравнения изгибающих моментов M_x(z) воспользуемся зависимостью между прогибом V(z) и моментом

M_x(z)=–EI (z),

где

Определим константы из граничных условий

V(0)= (0)=V(l)= (l)=0.

Тогда

а уравнение изгибающих моментов примет вид

Для нахождения уравнения крутящего момента M_k(z) воспользуемся зависимостью между углом закручивания θ(z) и крутящим моментом:

M_k(z)=GI_p'(z),

где

Определим θ(0) и M_k(0) из граничных условий θ(0) = 0 , θ(l) = 0 , тогда M_k(0)=0,5M=0,5Ph а уравнение M_k(z) запишем как

M_k(z)=0,5M–M=0,5Ph|_I–Ph|_II .

Графики изгибающих и крутящих моментов показаны на рис. 5.14. При z = l / 2 |M_x| = Pl/8 , |M_k| = Ph/2 , и выражение ( 5.17 ) примет вид

Принимаем диаметр d равным 5,1 см .

З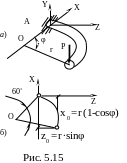 адача 14

На свободном конце плоской криволинейной консоли круглого поперечного сечения ( d = 5 см ) , ось которой очерчена по дуге окружности радиусом r = 50 см с центральным углом φ = 60°, действует сила Р перпендикулярно плоскости изгиба стержня ( рис. 5.15а ) . Найти допустимую силу [P] при условии , что допускаемое напряжение [σ] = 160 МПа .

Сила Р создает в опасном сечение А данного стержня напряжения изгиба и кручения . Эти напряжения определяются через величины изгибающего момента M_x=P∙z₀=P∙r∙sin и крутящего момента M_k=P∙x₀=P∙r∙(1-cos). При угле φ = 60 получим

Для расчета на прочность воспользуемся третьей и четвертой гипотезами прочности . Выражения ( 5.17 ) и ( 5.12 ) представим в виде

‚ . ( 5.18 )

Подставляя значения моментов M_x и M_k в ( 5.18 ) , получим

, .

Отсюда [P^III]4∙10 ^-3 МН , [P^IV]4,13∙10 ^-3 МН .

Допустимое значение необходимо принять равным [P] = 4000 Н .

Задача 15

Плоская прямоугольная стержневая система ( рис 5.16 ) квадратного сечения со стороной a = 2 см изгибается в плоскости чертежа . Зная длину ( l = 40 см ) и материал стержня ( [σ] = 200 МПа ) , определить величину допускаемой силы [P] из условия прочности .

П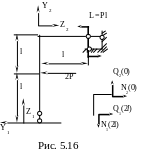 ри изгибе стержней касательные напряжения от поперечной силы малы по сравнению с нормальными [22] , поэтому для расчета можно воспользоваться любой теорией прочности . Величину продольных сил вычислим из условий равновесия сил в узле ( рис. 5.16б ) .

N₁(2l)=Q₂(0), N₂(0)=–Q₁(2l).

Тогда для опасного сечения условия прочности можно записать как

или

. ( 5.19 )

Запишем уравнения изгибающих моментов для каждого стержня

M₁(z)=M₁(0)+Q₁(0)z–2P(z–l), M₂(z)=M₂(0)+Q₂(0)z. ( 5.20 )

Учитывая силовые граничные условия и условия сопряжения

M₁(0)=0, Q₁(0)=0, M₁(2l)=M₂(0), M₂(l)=–L=–Pl,

представим ( 5.20 ) в виде

M₁(z)= , M₂(z)=–2Pl+ .

Из уравнений поперечных сил в каждом стержне найдем значения продольных сил :

Графики изгибающих моментов и продольных сил представлены на рис. 5.17.

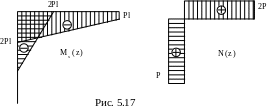
Запишем условие ( 5.19 ) для сечения с наибольшим изгибающим моментом |M_x|^max=2Pl и наибольшей продольной силой N = 2P :

,

отсюда

,

тогда

Задача 16

П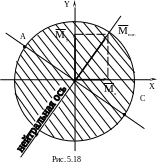 о известной схеме нагружения и передаваемой мощности определить диаметр круглого поперечного сечения вала , применяя третью теорию прочности .

В задаче будем использовать исходные данные и результаты решения задачи 7 ( см. гл. 2 ) при [σ] = 160 МПа .

По результатам решения задачи видно, что опасным является сечение С ( рис. 2.18 ) , в котором М_k = 1,2 кН∙м ; М_x = 7 кН∙м ; М_y = 10,5 кН∙м . При нагружении стержня круглого поперечного сечения двумя момен-тами ( М_x и М_y ) их можно свести к одному моменту  = 12,62 кН∙м , т.е. рассматривать вместо косого изгиба плоский.

На рис. 5.18 показан вектор изги-бающего момента; нейтральная ось будет совпадать с направлением вектора и наибольшие нормальные напряжения будут в точках А и С (наиболее удаленных от нейтральной оси)

_A=M_изг/W_x=M_изг/(0,1d³), _C=–M_изг/W_x=M_изг/(0,1d³).

Крутящему моменту в сечении В соответствуют наибольшие касательные напряжения в точках контура сечения _max=(M_k/I_p)_max=M_k/W_p=M_k/(0,2d³). Таким образом‚ опасными в сечении являются точки А и С. Для рассмотрения возьмем точку А ‚ в которой действуют нормальные напряжения σ_А и τ_А = τ_max‚ направленные по касательной к контуру сечения против хода часовой стрелки (при наблюдении c конца оcи Z) .

В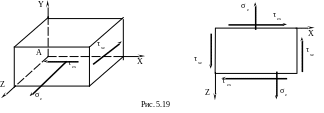 ыделим элемент деформируемого тела в окрестности точки А в форме прямоугольного параллелепипеда‚ совместив ось Y с прямой АС ( рис. 5.19 ).

Составляющие напряженного состояния в точке

_z=M_изг/W_x=M_изг/(0,1d³), _x=_y=0,

_zx=–_xz=–M_k/(0,2d³), _xy=_yz=0.

Определим главные напряжения , являющиеся корнями уравнения

³–I₁²+I₂–I₃=0,

где

После подстановки получим

³–_z²–_xz²=0;

его корни

Следовательно,

Условие прочности по третьей теории запишется в виде (₁–₃)[] или . Подставив выражения для напряжений , получим

,

отсюда

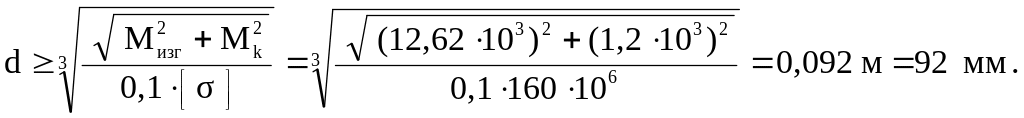
Принимаем диаметр d равным 95 мм .

Расчет на прочность толстостенных цилиндров и тонкостенных оболочек

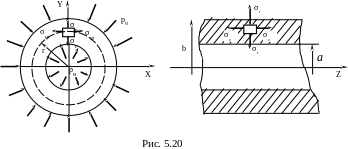
В любой точке толстостенного цилиндра , нагруженного равномерно распределенным внутренним p_В и внешним p_Н давлениями ( рис. 5.20 ) , возникают радиальные σ_r‚ окружные σ_φ и осевые σ_z ( при наличии днищ ) напряжения , которые определяют по формулам [10] :

( 5.21 )

( 5.22 )

( 5.23 )

где a и b - внутренний и наружный радиусы цилиндра ; r - текущий радиус .

Задача 17

Подобрать размер внешнего диаметра 2b цилиндра с днищами , находящегося под действием внутреннего давления p = 50 МПа , при коэффициенте запаса прочности, равном двум . Предел текучести материала цилиндра σ_Т = 500 МПа, коэффициент Пуассона μ = 0,3 , внутренний диаметр 2a = 10 см. Расчет вести по второй и третьей теориям прочности .

Давление p вызывает расширение цилиндра , поэтому наиболее опасными являются точки , расположенные на его внутренней поверхности ( r = a ) . Тогда , имея в виду, что p_Н = 0, p_В = p и r = a‚ напряжения, действующие в цилиндре , вычислим по формулам

( 5.21 ) – ( 5.23 ) :

Для заданного материала цилиндра допускаемое напряжение [σ] определим как

[]=0,5_T=250 МПа.

Тогда по третьей теории прочности получим

Откуда

Согласно второй теории прочности

Отсюда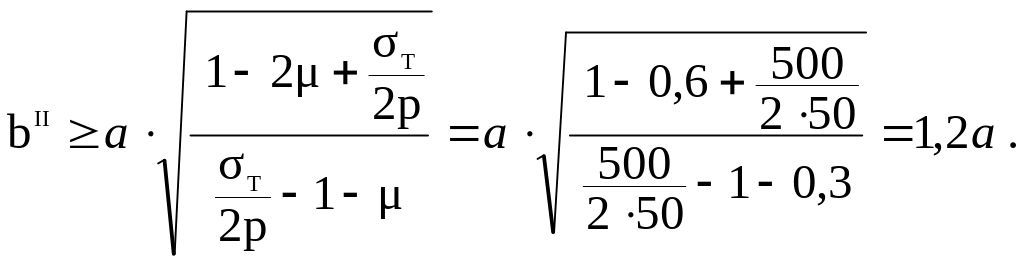

Удовлетворяя требованиям обеих теорий прочности, необходимо принять цилиндр с наружным диаметром 2b = 21,29a  13 см .

Задача 18

Н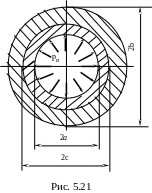 айти оптимальную величину давления натяга p составного цилиндрa, нагруженного внутренним давлением p_В ( рис. 5.21 ) , из условия равнопрочности внутреннего и наружного цилиндров . Определить также величину допускаемого давления p_В по четвертой теории прочности .

Дано :

a = 4 см, b = 8 см, c = 6 см, [ σ ] = 500 МПа .

Составной цилиндр можно изготовить так: разогреть наружный и вставить в него внутренний . При остывании наружный цилиндр напрессовывается на внутренний и создается осесимметричное давление натяга р на поверхности соприкосновения двух деталей ( r = c ) . Учитывая, что материал обоих цилиндров одинаков , условие нераскрытия стыка на поверхности контакта можно обеспечить , рассматривая стенку составного цилиндра как сплошную . Тогда по принципу независимости действия сил напряжения в любой точке составного цилиндра будут равны сумме напряжений от внутреннего давления и давления натяга . При этом наибольшие напряжения для внутреннего цилиндра будут соответствовать r = a :

Для наружного цилиндра напряжения будут наибольшими при r = c:

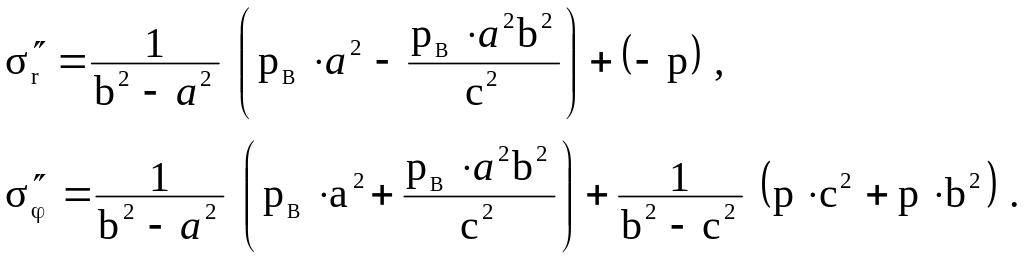
Подставив значения известных величин, получим

По четвертой теории прочности ( 5.13 ) при σ₁ = σ_φ, σ₂ = 0, σ₃ = σ_r получим

Условие равнопрочности цилиндров обеспечим , соблюдая условие

или

. ( 5.24 )

После несложных преобразований получим

4,28p_B²–24,6p∙p_B–4,36p²=0. ( 5.25 )

Решением этого уравнения будет p_B=5,91p .

Давление от натяга найдем из первого радикала уравнения ( 5.24 ) :

.

После подстановки выражения ( 5.25 ) получим 10,5p[] . Отсюда найдем давление натяга

Тогда величина допускаемого внутреннего давления

p_В = 5,91p = 281,4 МПа .

З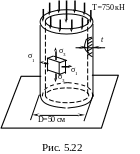 адача 19

Вертикально стоящий цилиндрический сосуд наружным диаметром 50 см испытывает внутреннее рабочее давление p = 2 МПа и нагружен через днище вертикальными силами , равномерно распределенными по его торцу . При этом равнодействующая вертикальных сил составляет 750 кН ( рис. 5.22 ) . Устойчивость конструкции обеспечивается жесткими ребрами и диафрагмами , не показанными на рисунке . Определить толщину t стенки сосуда , если допускаемое напряжение [σ] = 80 МПа и принята

четвертая теория прочности . Какая необходима толщина t , если бы была принята третья теория прочности?

С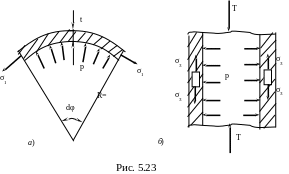 читая конструкцию тонкостенной, рассмотрим равновесие элемента оболочки ( рис. 5.23 ) . Спроектируем все действующие силы на направление радиуса( рис. 5.23 а ):

Принимая угол dφ малым , получим

₁=pR/t.

Напряжения вдоль образующей ( рис. 5.23 б ) получим из алгебраической суммы напряжений , вызванных внутренним давлением и сжимающей силой Т :

Вычислим напряжения σ₁ и σ₃ как

Тогда условие прочности ( 5.13 ) примет вид

или

Отсюда t0,6449/80=8,06∙10 ^–3 м  8 мм .

Если применить третью теорию прочности , то из (5.12) после подстановки значений σ₁ и σ₂ получим 0,5/t+0,228/t80‚ отсюда t9,73∙10 ^–3 м  10 мм .

Использование четвертой теории прочности приводит к уменьшению веса конструкции .

Задача 20

Н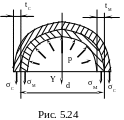 а полый медный цилиндр с внешним диаметром d = 50 см и толщиной стенки t_М = 4 мм плотно насажен полый стальной цилиндр с толщиной стенки t_С = 2 мм . Определить наибольшее допус-каемое внутреннее давление p в этом сосуде , если для меди [σ_М] = 40 МПа , Е_М = 10 ⁵ МПа , а для стали [σ_С] = 160 МПа , Е_С = 2∙10 ⁵ МПа. Напряжением вдоль оси цилиндров пренебречь .

Учитывая тонкостенность обоих цилиндров , разностью между внешним и внутренним диаметрами цилиндров пренебрегаем . При этом относительные деформации диаметров и периметров обоих цилиндров одинаковы :

_С=_М_С/E_C=_M/E_M.

Тогда ( 5.26 )

Рассмотрим равновесие элемента трубы . Для этого рассечем её диаметральной плоскостью ( рис. 5.24 ) и спроектируем все действующие силы на ось Y :

2_M∙t_M+2_C∙t_C–p∙d=0. ( 5.27 )

С учетом соотношения ( 5.26 ) получим 2_M∙t_M+4_M∙t_C–p∙d=0. Отсюда

p=2_M∙(t_M+2t_C)/d .

Примем σ_М = [σ_М] , тогда

p=2∙40∙(4∙10 ^–3+2∙2∙10 ^–3)/0,5=1,28 MПа .

В заключение отметим, что уравнение ( 5.27 ) нельзя решать относительно σ_С. Это связано с тем, что при давлении p , вызывающем в стальном цилиндре напряжение σ_С = 160 МПа , в медном цилиндре напряжение σ_М будет равно [σ_С]/2 = 160/2 = = 80 МПа . А это напряжение больше допускаемого для меди [σ_М] = 40 МПа .