В расчетах используется выражение

, ( 5.13 )

где I ₁ и I ₂ – первый и второй инварианты напряженного состояния. Как и третья теория прочности, энергетическая теория справедлива в основном при анализе напряженного состояния упруго – пластических тел.

При исследовании напряженного состояния материалов, неодинаково сопротивляющихся растяжению и сжатию, можно использовать пятую теорию прочности  теорию Кулона – Мора:

, ( 5.14 )

где к =  _р /  _сж – коэффициент, учитывающий отношение предела прочности на растяжение  _р к пределу прочности на сжатие  _сж.

Пятая теория прочности имеет существенное преимущество перед первой и второй теориями, которые на практике применяются редко. Она удовлетворительно описывает поведение пластичных материалов.

Рассмотрим на примерах вычисление напряжений, их распределение по сечениям стержней, расчеты на прочность.

Примеры решения задач

Задача 1

Для заданного стержня с указанным поперечным сечением вычислить максимальные нормальные напряжения. Построить график распределения напряжений по длине стержня при следующих данных. Поперечное сечение – квадрат со стороной а = 2 см, Р = 30 кН, q = 20 кН/м, l = 0,75 м.

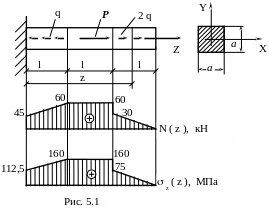
1) Вычислим интегральные характеристики напряжений:

N ( z ) = N ₀ + q z  q ( z – l ) – P ( z – 2 l ) ⁰ – 2 q ( z – 2 l ).

Из граничного условия на свободном конце стержня определим N ₀.

N ( 3 l ) = 0  N ₀ = 45 кН.

Вычислим значения интегральных характеристик напряжений в характерных точках стержня.

N ( 0 ) = 45 кН, N ( l ) = N ₀ + q l = 60 кН,

N (  2 l ) = N ₀ + 2 q l – q ( 2 l – l ) = 60 кН, N (  2 l ) = 30 кН,

N ( 3 l ) = N ₀ + 3 q l – q ( 3 l – l ) – P – 2 q ( 3 l – 2 l ) = 0.

По этим значениям строим график N ( z ) ( рис. 5.1 ).

2. Вычислим напряжения в сечениях по длине стержня.

, .

, , .

По этим значения строим график  _z ( z ) ( рис. 5.1 ).

Задача 2

Из условия прочности определить размеры квадратного поперечного сечения стержня. Схема нагружения приведена в задаче 2 ( рис. 2.9 ) ( см. гл. 2 ).

Дано: [  ] = 160 МПа, q = 60 кН/м, l = 0,4 м.

По эпюре N ( z ) ( рис. 2.9 б ) в опасном сечении возникает

.

Из условия прочности

, .

Если сторону квадрата сечения обозначить а, то

.

Задача 3

Определить площадь поперечного сечения F ( z ) стержня из условия равнопрочности всех его сечений ( рис. 5.2 ).

Дано: Р ₁ = 50 кН, Р ₂ = 25 кН, [  ] = 150 МПа.

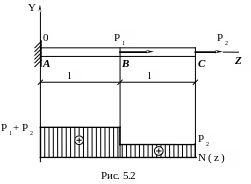
Действующие силы Р ₁ и Р ₂ вызывают растяжение стержня. При этом в его поперечном сечении возникают только нормальные напряжения  _z = N / F, а касательные напряжения равны нулю. Поэтому условие прочности можно записать в виде  _экв =   _z  _max  [  ]. Здесь   _z  =  N  _max / F – наибольшее напряжение в поперечном сечении стержня.

Для определения максимальной продольной силы  N _max составим уравнение N ( z ) по участкам:

, .

Для обеспечения условия равнопрочности всех сечений стержня необходимо соблюдать равенство нормальных напряжений во всех сечениях:

N ^{A B} / F _{A B}  [  ], N ^{B C} / F _{B C}  [  ],

отсюда

; .

; .

Задача 4

К стержню с поперечным сечением в форме эллипса приложены два сосредоточенных момента ( 2 L и L ) и распределенная моментная нагрузка интенсивностью m. Вычислить максимальные касательные напряжения при следующих данных:

L = 20 кН∙м, т = 16 кН∙м/м, l = 0,75 м, b = 7 см, а = 5 см.

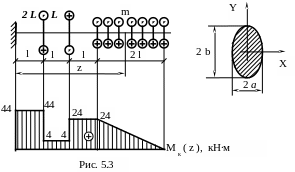
Вычислим интегральные характеристики напряжений:

M _к ( z ) = M ₀ – 2 L ( z – l ) ⁰ + L ( z - 2 l ) ⁰ – m ( z – 3 l ).

Из граничного условия на свободном конце стержня определим М ₀.

M ( 5 l ) = 0  M ₀ – 2 L + L – m 2 l = 0. M ₀ = 44 кН∙м.

Вычислим значения интегральных характеристик в характерных точках стержня.

M _к ( 0 ) = M ₀ = 44 кН∙м,

М _к (  l ) = M ₀ = 44 кН∙м, М _к (  l ) = M ₀ – 2 L = 4 кН∙м.

М _к (  2 l ) = М ₀ – 2 L = 4 кН∙м, М _к (  2 l ) = М ₀ – 2 L + L = 24 кН∙м,

М _к ( 3 l ) = M ₀ – 2 L + L = 24 кН∙м, М _к ( 5 l ) = M ₀ – 2 L + L + m 2 l = 0.

По этим значениям строим графики М _к ( z ) (рис. 5.3).

Вычислим касательные напряжения в опасном сечении стержня.

Максимальные касательные напряжения будут на концах малой оси эллипса и определяются по формуле

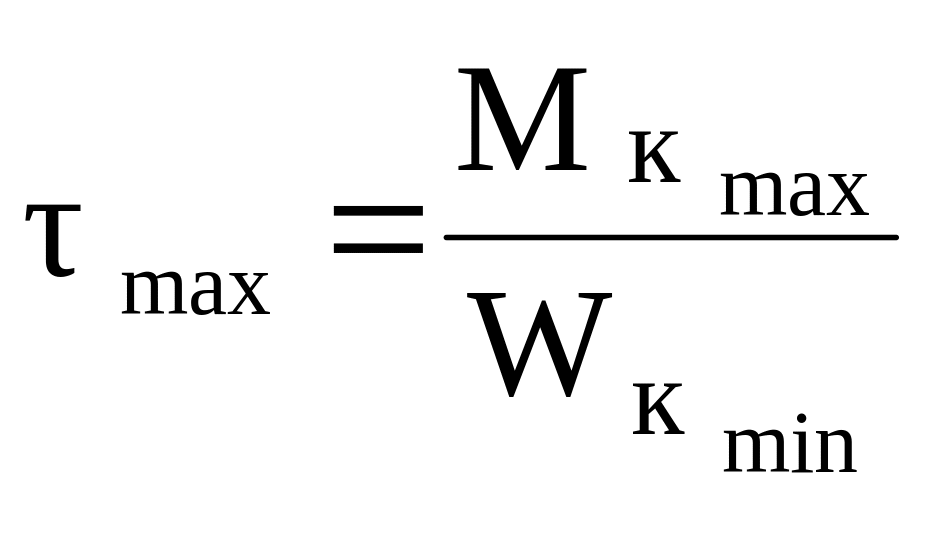, = 44 кН∙м, ,

.

На конце большой полуоси эллипса касательные напряжения

.

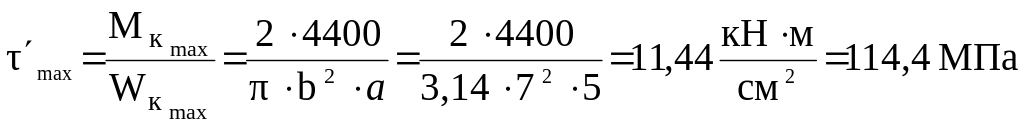Касательные напряжения на концах малой полуоси больше напряжений на концах большой полуоси в 1,33 раза

Задача 5

Определить максимальные касательные напряжения в стержне с сечением в форме равностороннего треугольника со стороной a при следующих исходных данных: L = 8 кН∙м ‚ m = 10 кН∙м / м, l = 2 м, a = 20 см.

1. Вычислим интегральные характеристики напряжений:

.

Из граничного условия на свободном конце в стержне определяем M ₀.

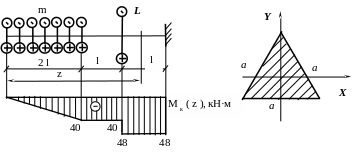
Рис. 5.4

Вычислим значения интегральных характеристик напряжений в характерных точках:

кН∙м.

кН∙м, кН∙м,

кН∙м.

По этим значениям строим график M _к ( z ) ( рис. 5.4 ).

2. Вычислим максимальные касательные напряжения, которые имеют место на серединах сторон треугольника.

кН∙м = 4 800 кН∙см,

= 120 МПа.

Задача 6

Используя третью теорию прочности, найти размеры круглого кольцевого сечения вала, если L = 0,5 m l = 10 кН∙м, m = 40 кН∙м/м, l = 0,5 м, [  ] = 160 МПа, D = 2 d, где D и d – наружный и внутренний диаметры сечения. Схема нагружения вала дана в задаче 4 ( гл. 2, рис. 2.15а ).

В опасном сечении вала крутящий момент . Наибольшие касательные напряжения будут в точках наружного контура ( рис. 5.5 ):

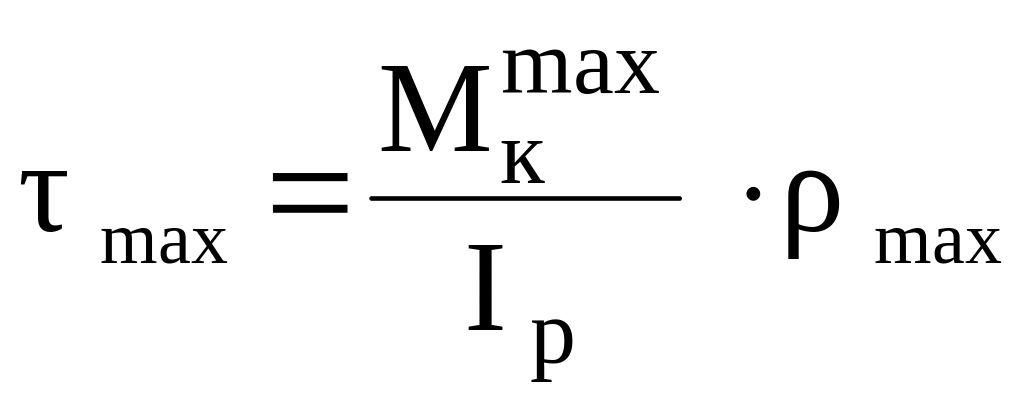
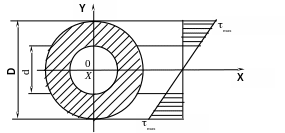
Рис. 5.5

Для кольцевого круглого сечения полярный момент инерции

тогда .

В опасных точках напряжённое состояние будет характеризоваться главными напряжениями  ₁ =  ,  ₂ = 0 ,  ₃ = –  ; т. е. напряжённое состояние будет двухосным.

По третьей теории прочности или

Тогда

и

Задача 7

Определить размеры круглого поперечного сечения стержня d по третьей и четвертой теориям прочности.

Дано: L = 30 кН∙м, m = 10 кН∙м/м, l = 1 м, [  ] = 200 МПа.

Y

Z X

2

l l

Y I II

m L

d

M _к ( z ), ml

1

При кручении круглого стержня в любом его сечении возникают только касательные напряжения

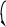
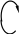
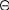
где M _к – крутящий момент в попереч-ном сечении стержня; I _p =  d ⁴ / 32 – поляр-ный момент инерции круглого сечения; 0    d / 2 – полярный радиус сечения.

Очевидно ‚ что наибольшее напряжение возникает в точках ‚ расположенных в на- ружных слоях сечения (  =  _max = 0,5 d ).

Тогда

где W _p  0,2 d ³ – полярный момент сопротивления круглого сечения.

Условия прочности ( 5.12 ) при  ₂ = 0, запишем как

( 5. 15 )

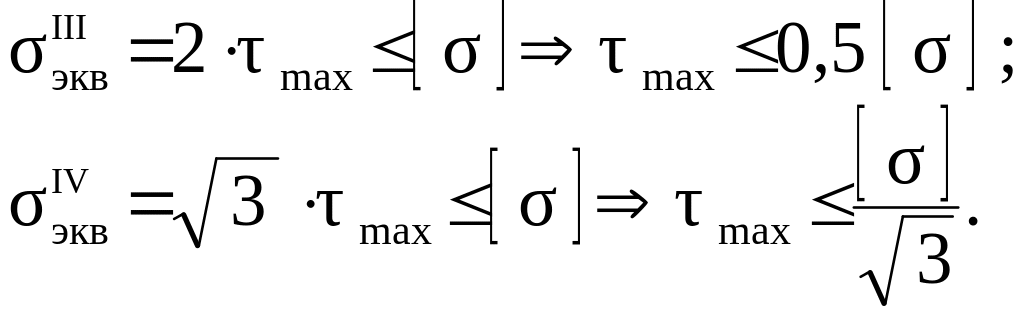
C учетом L = 3 m l уравнение крутящих моментов примет вид

График M _к ( z ) представлен на рис. 5.6.

Теперь находим  _max = 2 m l / W _p, и условие прочности ( 5.15 ) представим в виде

Принимаем d = 10 см.

Задача 8

Для заданной балки с указанным поперечным сечением вычислить максимальные нормальные и касательные напряжения, построить графики их распределения по высоте сечения при следующих данных: q = 10 кН/м, P = 20 кН, L = 20 кН∙м, l = 1 м, а = 4 см.

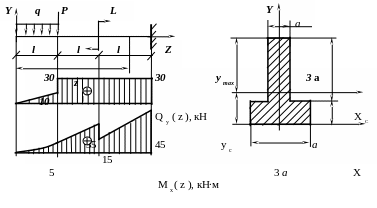
Рис. 5.7

1. Вычислим интегральные характеристики сечения:

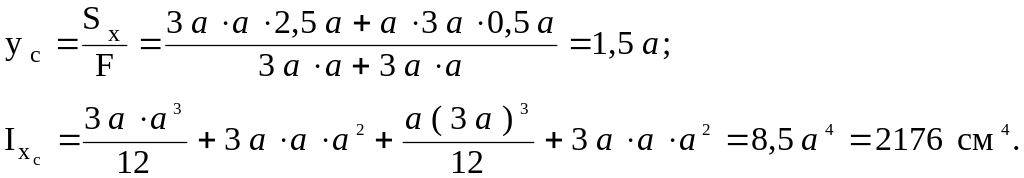
2. Вычислим интегральные характеристики напряжений:

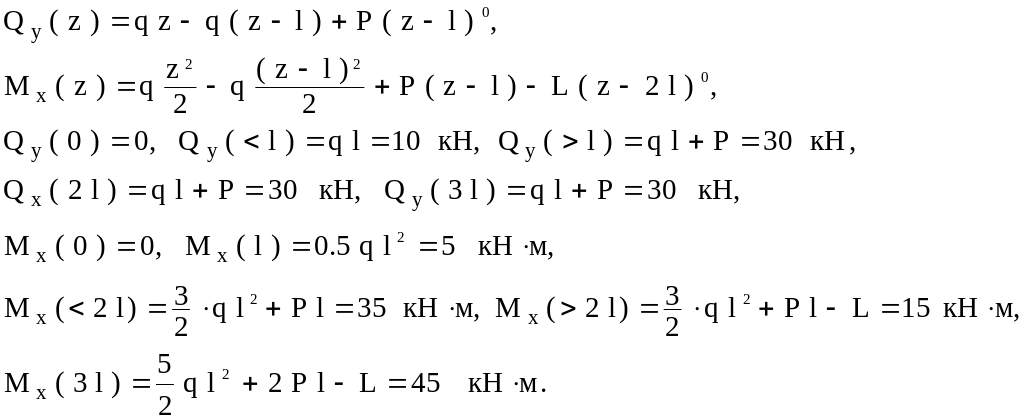
По этим данным строим графики и ( рис.5.7 ). Опасное сечение находится в заделке, где Максимальные нормальные напряжения в сечении будут при

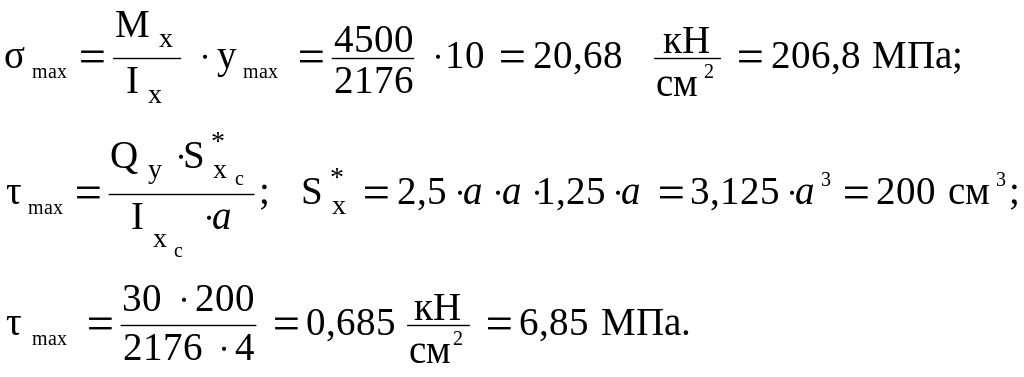
Построим графики  и  по высоте сечения ( рис. 5.8 ).

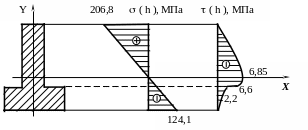
Рис. 5.8

В нижнем слое нормальные напряжения

Касательные напряжения на переходе к горизонтальной полке

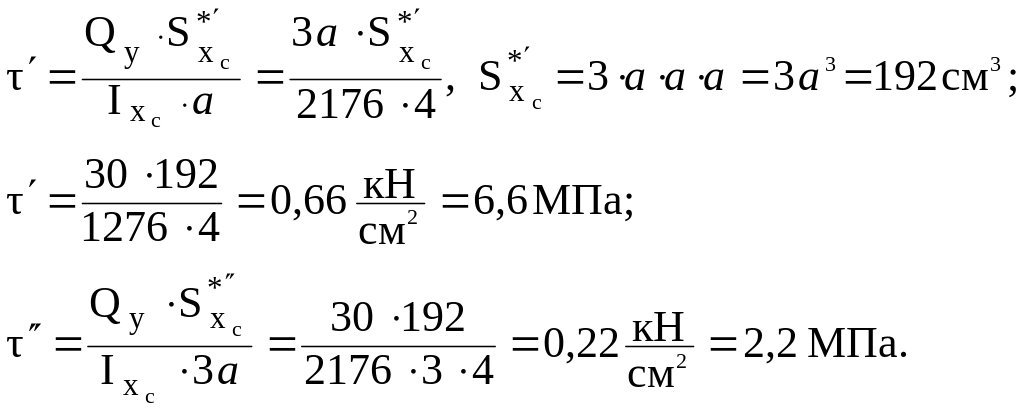
Задача 9

Проверить прочность балки, схема нагружения которой представлена в задаче 5, ( гл. 2 ), если l = 1 м, q = 20 кН/м, [  ] = 160 МПа. Поперечное сечение балки состоит из швеллера № 14 и уголка № 8; геометрические характеристики определены, в частности I _x = 707 см ⁴. Плоскость действия внешних нагрузок совпадает с плоскостью главных центральных осей поперечных сечений.

Поскольку нагрузки действуют в плоскости YOZ, то имеем поперечный изгиб. Нормальные напряжения определяются по формуле  = ( M _x y / I _x ), а проверка прочности заключается в выполнении условия  _max  [ ]. Из эпюры M _x ( z ) следует, что _, а наибольшие напря-жения в опасном сечении будут в точке, имеющей наибольшую координату " y ".

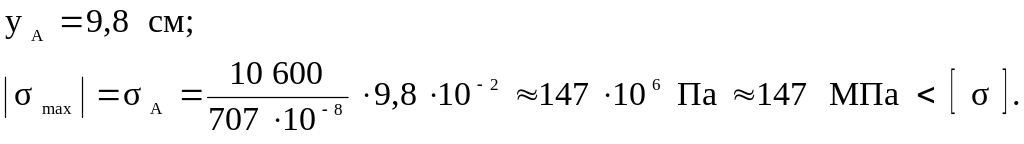
Таким образом, условие прочности выполнено.