4.Общая математическая модель деформирования упругих тел
Если упругое тело нагружено внешними нагрузками, то в нем происходят следующие взаимосвязанные процессы.
1.
В каждой точке тела возникают различные
по величине и направлению ВСФ -
,
,
,
,
,
.
Интенсивности этих ВСФ позволяют
оценивать напряжения в каждой точке
тела. Если поведение тела рассматривать
в прямоугольной декартовой системе
координат, то в каждой его точке в общем
случае возникают девять составляющих
полного напряжения - три нормальных
напряжения (
)
и шесть касательных напряжений, три
пары которых равны между собой (
).
В каждой точке тела напряжения различны
по величине и направлению. Таким образом,
напряженное состояние в точке
деформируемого тела можно оценить
шестью величинами:
а) тремя нормальными напряжениями
б) тремя касательными напряжениями
Значения напряжений в теле и выбор сечений, где они максимальны, позволяют оценивать на стадии проектирования или эксплуатации меру сопротивления тел внешним нагрузкам, что определяется с помощью проектных или проверочных расчетов на прочность.
Рассмотрение равновесия деформируемого тела приводит к системе из трех уравнений равновесия:
(4.1)
где X, Y, Z – проекции массовых сил тела на оси x, y, z.
Ясно, что отыскать из решения системы трех дифференциальных уравнений в частных производных шесть напряжений невозможно. Поэтому рассмотрение силового
аспекта процесса деформирования оставляет открытым вопрос о степени сопротивляемости тел внешним нагрузкам как в упругой, так и в пластической областях деформаций.
2.
При воздействии на тело внешними
нагрузками оно деформируется, т.е.
изменяются его размеры и форма. В общем
случае каждая точка тела может совершать
сложное перемещение
,
,
одновременно в направлении координатных
осей
,
,
,
а сечения тела могут поворачиваться на
углы
,
,
относительно этих осей. Деформации тела
можно оценивать с помощью относительных
линейных деформаций
,
,
,
а угловые - с помощью относительных
угловых деформаций
,
,
,
,
,
,
три пары которых равны. Значит,
деформированное состояние в каждой
точке тела характеризуется шестью
составляющими:
а) тремя относительными линейными деформациями
,
,
,
б) тремя относительными угловыми деформациями
Рассмотрение геометрических соотношений при деформировании тела приводит к шести уравнениям Коши (3.20), связывающим линейные перемещения тела и относительные деформации:
Полная информация о деформированном состоянии тела известна, если в каждой его точке известны девять составляющих:
Очевидно, что, рассматривая только геометрический аспект процесса деформирования из системы шести уравнений (3.20) отыскать девять неизвестных невозможно.
Не
удается вычислить составляющие
напряженного состояния (
,
,
,
,
,
)
и деформированного
состояния (
,
,
,
,
,
,
,
,
)
рассматривая эти процессы совместно,
так как системы уравнений (3.20) и (4.1) –
это девять уравнений, а подлежат отысканию
пятнадцать неизвестных величин.
Разрешить эту задачу можно, рассмотрев физическую сторону процесса деформирования, что позволит связать компоненты напряженного и деформированного состояний. Такие зависимости известны и согласно закону Гука (3.32) имеют вид
где Е и G – модули упругости материала первого и второго рода;
– коэффициент
поперечной деформации (коэффициент
Пуассона);
– первый
инвариант напряженного состояния.
Рассматривая все аспекты процесса деформирования (силовой, геометрический и физический), можно прийти к следующей системе уравнений:
,
,
,
,
,
,
,
,
,
,
,
.
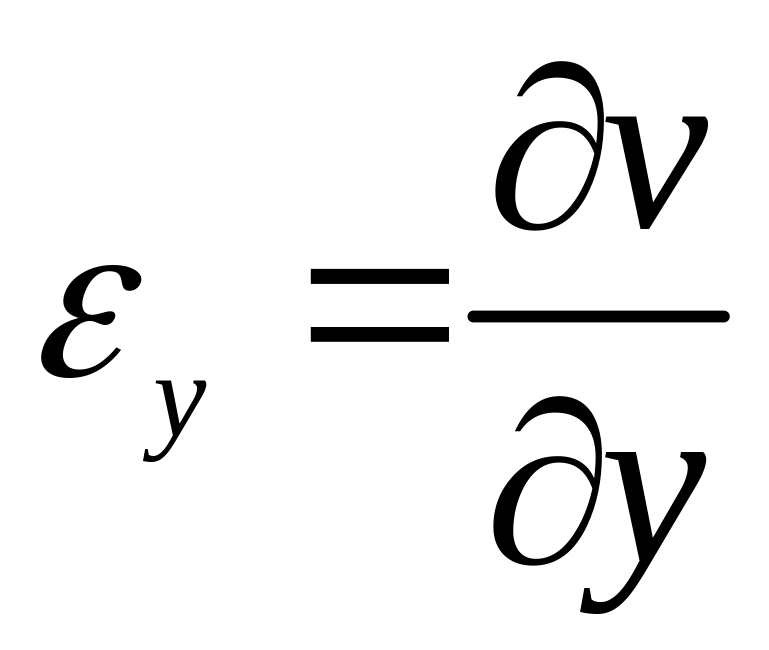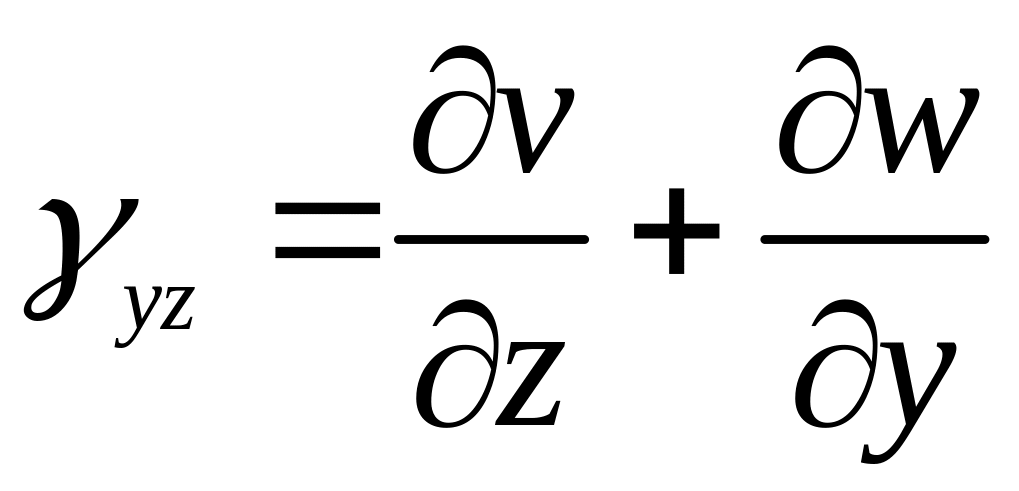(4.2)
Систему из пятнадцати уравнений (4.2) называют математической моделью процесса деформирования упругого тела. В силу основной теоремы алгебры из решения этой системы уравнений можно отыскать пятнадцать неизвестных: , , , , , , , , , , , , , , , однозначно определяющих напряженно-деформированное состояние в каждой точке тела. Это дает возможность проводить любые расчеты (на прочность, жесткость, устойчивость, колебания и т.д.), позволяющие судить о различных аспектах безопасности эксплуатации исследуемых объектов.
В системе уравнений (4.2) первые девять уравнений – дифференциальные уравнения в частных производных. Значит, при решении системы (4.2) необходимо проводить интегрирование, в результате которого появятся новые неизвестные, помимо пятнадцати, подлежащих отысканию. Эти дополнительные неизвестные отыскивают, привлекая некоторые условия, каковыми являются граничные условия и начальные условия (если рассматривается динамическая задача).
Ясно, что решение системы уравнений (4.2) сложно и к настоящему времени его общего решения не получено. Для прикладных инженерных задач при определенных допущениях о свойствах тел и способах их нагружения решены некоторые частные задачи. Вместе с тем решение этих частных задач позволило создать на практике достаточно надежные методы оценки различных параметров деформирования реальных тел.
В частности, известны задачи Сен-Венана. Эти задачи рассматривают напряжения и деформации, возникающие в призматических телах, имеющих произвольные поперечные сечения. Решение задач Сен-Венана осуществляется:
1) прямым методом, когда напряжения и деформации находят при известных граничных условиях;
2) обратным – по известным составляющим тензоров напряжений и деформаций устанавливают граничные условия, которым эти составляющие должны удовлетворять;
3) полуобратным – по частично известным напряжениям и деформациям определяют оставшиеся при частично известных граничных условиях.
Первые два метода требуют значительного математического аппарата.
Рассмотрим подробнее частную задачу, вытекающую из рассмотрения соотношений (4.2): плоскую задачу о деформировании прямого стержня.
Пусть
на стержень действуют нагрузки
и
,
приложенные в силовых плоскостях,
совпадающих с главными центральными
осями сечений.
Математическая модель для такой задачи приводит к двум дифференциальным уравнениям:
(4.3)
Уравнения (4.3) называют основными уравнениями для прямого стержня. Каждое из уравнений (4.3) может быть использовано самостоятельно для анализа процесса деформирования.
Рассмотрим некоторые частные случаи, вытекающие из рассмотрения уравнений (4.3).
1. Если
,
а
,
то система (4.3) сводится к уравнению
(4.4)
характеризующему растяжение (сжатие) стержней. По закону Гука
(4.5)
Тогда приходим к уравнению
(4.6)
Уравнение
(4.6) определяет математическую модель
стержня при растяжении (сжатии) и
позволяет при решении отыскать перемещения
сечений стержня, а по ним нормальные
силы
,
напряжения
,
проводить расчеты на прочность или
жесткость.
2. Если
внешняя нагрузка
,
т.е. зависит еще и от перемещений самого
стержня, то приходим к задаче о растяжении
(сжатии) стержня в упругой среде. При
внешней нагрузке
(4.7)
где С – жесткость упругой среды, где перемещается стержень, получим уравнение
(4.8)
Уравнение
(4.8) определяет растяжение (сжатие)
стержня в среде с жесткостью С и позволяет
при решении отыскать
,
,
и проводить расчеты на прочность и
жесткость.
3. Внешняя нагрузка может зависеть не только от координаты «z», но и от времени «t», т.е. может быть динамической:
(4.9)
Известно, что при действии динамических нагрузок возникают силы инерции, которые могут быть определены как
(4.10)
где
- масса единицы объема стержня, F –
площадь поперечного сечения стержня.
При подстановке выражения (4.10) в (4.6) получим уравнение при постоянной жесткости EF стержня
(4.11)
Уравнение
(4.11) – математическая модель вынужденных
продольных колебаний стержня. Его
решение позволяет отыскивать
или
.
Если
внешние нагрузки
не действуют в течение всего процесса
деформирования, а приложены к стержню
кратковременно, а затем сняты, то (4.11)
приводится к виду
(4.12)
где
.
Уравнение (4.12) определяет
свободные продольные колебания стержня.
Размерность коэффициента
метр в секунду указывает на возможность
оценки с помощью этого уравнения скорости
распространения упругой продольной
волны в стержне и, значит, скорости
распространения звука.
4. Если
рассмотреть защемленный с одной стороны
и свободный с другой, стержень длиной
,
нагруженный силами собственного веса
(γ - объемная плотность материала стержня,
F – площадь поперечного сечения), то на
него действует полный вес
.
Если потребовать, чтобы во всех его
сечениях нормальные напряжения σ были
одинаковыми, то при использовании (4.6)
получим уравнение вида
(4.13)
где
– площадь поперечного сечения на крайнем
свободном конце стержня.
Уравнение (4.13) определяет стержень равного сопротивления, оно используется, в частности, в строительстве при проектировании колонн, опор, обеспечивая их безопасную эксплуатацию.
Когда из внешних нагрузок только , для анализа деформирования стержней можно использовать первое из уравнений (4.3), которое принимает вид
(4.14)
В зависимости от
характера внешней нагрузки
это уравнение приводит к ряду других
частных уравнений, являющихся
математическими моделями деформирования
стержней при их поперечном изгибе.
1. При
имеет место плоский поперечный изгиб
(см. гл. 5).
2. При
(где С – жесткость среды) (4.14) приводится
к уравнению
(4.15)
Уравнение (4.15) является математической моделью поперечного изгиба стержня в упругой среде. В литературе такой класс задач называют «изгибом балки на упругом основании». Его результаты используют, в частности, при проектировании железнодорожных и трамвайных путей.
3. При
уравнение (4.15) при постоянной жесткости
приводится к виду
(4.16)
Уравнение (4.16) является математической моделью вынужденных поперечных колебаний стержня с постоянной жесткостью.
Если
,
то первое из уравнений (4.3) преобразуется
к виду, описывающему свободные поперечные
колебания стержней:
(4.17)
4. При , первое из уравнений (4.3) приводится к виду
(4.18)
Уравнение (4.18) описывает явления, связанные с потерей устойчивости стержней.
5. При , первое из уравнений (4.3) позволяет анализировать продольно-поперечный изгиб стержней.
Совместное решение
системы уравнений (4.3) при конкретных
значениях внешних нагрузок
и
приводит к возможности рассматривать
широкий круг задач, в частности
динамических.