2.4. Расчет поперечных ребер
Поперечные ребра запроектированы с шагом l1=98см. Ребро рассчитываем как балку таврового сечения с защемленной опорой.
Постоянная расчетная нагрузка с учетом веса 1 м ребра (см. рис. 1),
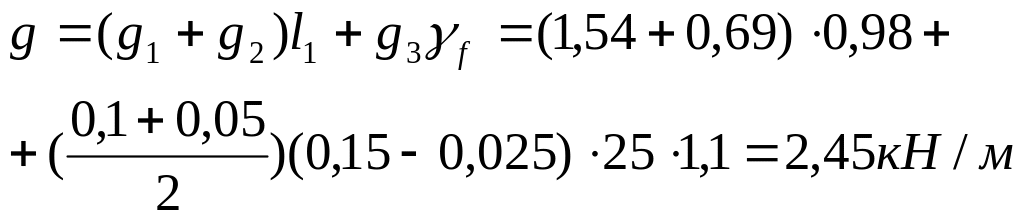
Снеговая нагрузка
кН/м
Полная нагрузка
кН/м
Изгибающие моменты в пролете и на опоре:
кН·м=191
кН·см
Поперечная сила:
кН
Полезная высота сечения ребра h0=h-a=15-2,5=12,5 см. Расчетное сечение поперечного ребра – тавровое с полкой в сжатой зоне:
см
Коэффициент
По табл. П.4.1
принимаем
и
.
Уточняем:
Нейтральная ось проходит в полке. Требуемая площадь сечения рабочей арматуры класса А-I
см2
Принимаем 1 Ø10 А-1,
см2.
При равенстве опорных и пролетных моментов верхний стержень каркаса КР2 принимаем как нижний, т.е. 1 Ø10 А-1, см2.
Проверяем несущую способность сечения ребра на поперечную силу из условия работы бетона на растяжение:
следовательно, расчет поперечной арматуры не требуется. Устанавливаем конструктивно поперечные стержни Ø3Вр-І с шагом 150 мм.
2.5. Расчет продольных ребер
Расчетный пролет панели при ширине опоры 10 см:
Полная расчетная
нагрузка (см. табл. 1)
4,4
кН/м2
Приведенная ширина двух продольных ребер 16 см (см. рис.1)
Расчетная ширина полки таврового сечения (рис. 2)
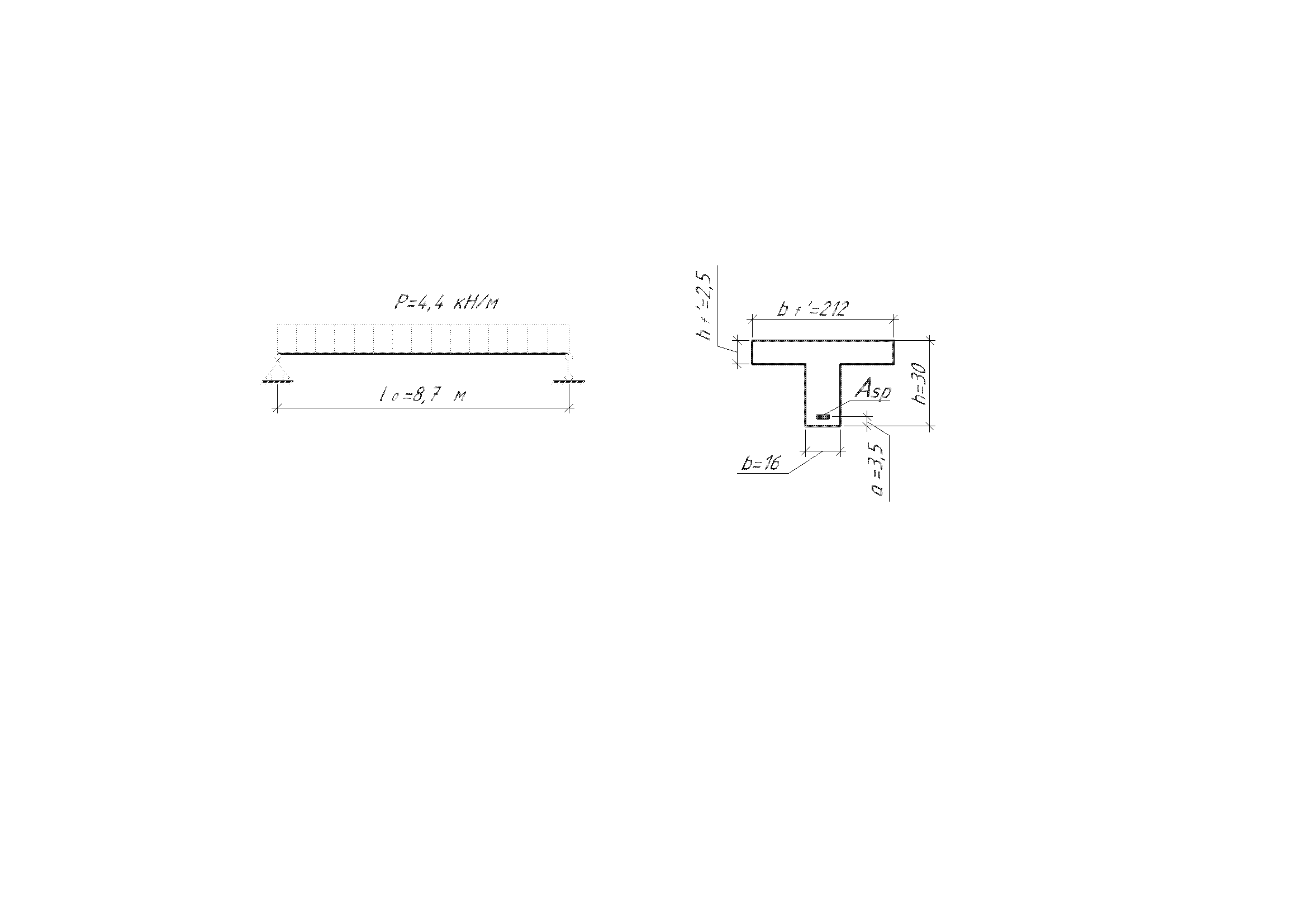
Рис.2
Максимальный изгибающий момент
кН·м=5401
кН·см
где
-
номинальная ширина панели.
Рабочая высота
панели 
см.
Расчетный случай таврового сечения:
кН·см
кН·см
следовательно,
условие соблюдается. Нейтральная ось
проходит в пределах полки, т.е.
.
Вычисляем коэффициент
как
для элемента прямоугольного сечения
шириной
:
По табл. П.4.1 находим
.
Требуемая площадь
сечения напрягаемой арматуры класса
Ат-V (
=68
кН/см2) при
:
(для арматуры
класса А-IV
= 1,2; классов А-V, В-II, Вр- II, К-7 и
К-19
=1,15;
класса А-VI
=1,1).
По сортаменту
(табл.
П.2.6
и
П.2.7)
принимаем
2Ø14
Ат-V,
=
3,08 см2 и располагаем по одному
стержню в
каждом
ребре.
Коэффициент
армирования
Процент
армирования
Расчет прочности по сечениям, наклонным к продольной оси.
Поперечная сила в опорных сечениях продольных ребер панели:
кН
Влияние свесов сжатой полки:
Вычисляем
кН·см
В расчетном
наклонном сечении
отсюда
см
см. Принимаем с=53 см. Тогда
кН;
следовательно, поперечная арматура по расчету не требуется.
При
450 мм на приопорных участках продольных
ребер, равных 1/4 пролета, поперечные
стержни устанавливаем конструктивно
3Ø
Вр-I
с шагом =
=15
см (
15
см). На остальной части пролета -
=3/4h
=
=
22,5 см. Принимаем s1
= 15 см; s2= 20
см. Рекомендуется шаг поперечных стержней
принимать кратным 5 см, причем в сторону
уменьшения. Поперечные стержни объединяем
в каркас КР1 специальными монтажными
продольными стержнями 2Ø8 А-I.
2.6. Расчет панели по образованию трещин
Геометрические характеристики приведенного сечения
Коэффициент
приведения для напрягаемой арматуры
Площадь приведенного сечения (рис. 3)
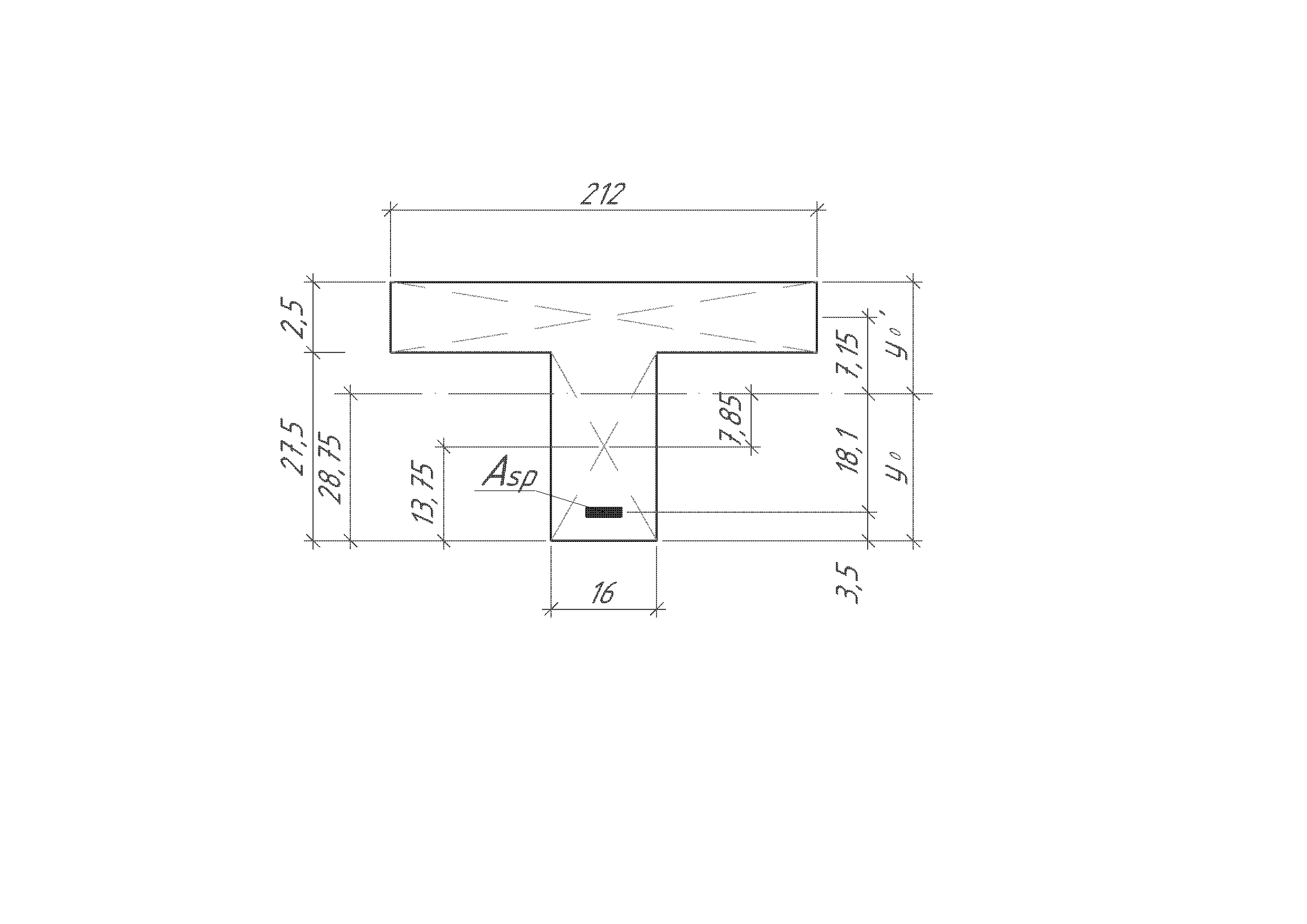
Рис. 3
см2
Статический момент приведенного сечения относительно нижней грани:
Расстояние от нижней грани сечения до центра тяжести:
см
Расстояние от
верхней грани сечения до центра тяжести:
см
Момент инерции приведенного сечения:
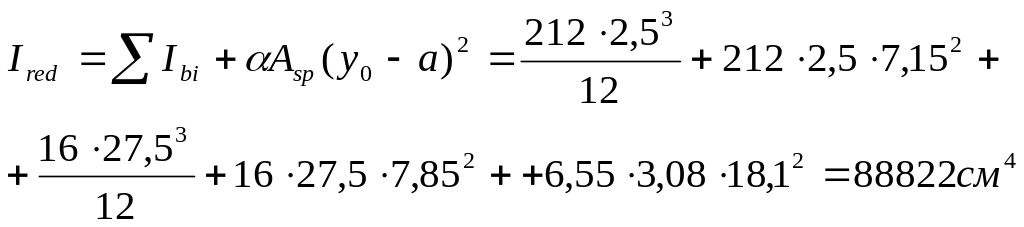
Момент инерции
для каждой простой фигуры (рис.
3) подсчитывается относительно
собственной оси 
и относительно центра тяжести приведенного
сечения.
Эксцентриситет приложения силы обжатия
см
Определение потерь предварительного напряжения арматуры
Первые потери напряжения:
от релаксации
напряжений в арматуре
кН/см2.
Значение
приведено в исходных данных для расчета
панели. Для арматуры из высокопрочной
проволоки
от разности
температур напрягаемой арматуры и
натяжных устройств (при Δ
t=65
°С)
кН/см2
от деформации
анкеров (при
=
2 мм)
кН/см2
где l= 700 см - длина напрягаемого стержня;
от быстро натекающей ползучести
кН
кН/см2
при
,
где
- передаточная прочность бетона (см.
исходные данные);
;
2,7
МПа = 0,27 кН/см2 (при
,
,
где
,
но не более 2,5 и не менее1,1)
Первые потери составляют:
кН/см2
Вторые потери:
от усадки бетона
класса В30, повергнутого тепловой
обработке,
МПа=
3,5 кН/см2 (для тяжелого бетона
классов В35 и ниже
МПа, В40 –
МПа, В45 и выше
МПа,
для легкого бетона на мелком плотном
заполнителе
МПа, пористом заполнителе –
МПа)
от ползучести бетона:
кН
кН/см2
при
МПа = 1,02 кН/см2
, где
для бетона, повергнутого тепловой
обработке при атмосферном давлении.
Вторые потери составляют
кН/см2
Полные потери:
кН/см2
Сила
обжатия при
:
кН
Момент
сопротивления сечения относительно
нижних волокон:
см³
Расстояние от ядровой точки, наиболее удаленной от растянутой зоны до центра тяжести приведенного сечения:
см
Упругопластичний
момент сопротивления сечения с полкой
в сжатой зоне:
см³
Изгибающий
момент при образованы трещины:
кН·см= =46,35 кН·м, где
кН·м
Момент от полной нормативной нагрузки:
кН·см
Так как
,
в нижней зоне панели трещины не образуется.
Если неравенство
не соблюдается, т. е.
,
то необходимо выполнить расчет панели
по раскрытию трещин. Для этого вычисляется
момент от длительной нормативной
нагрузки
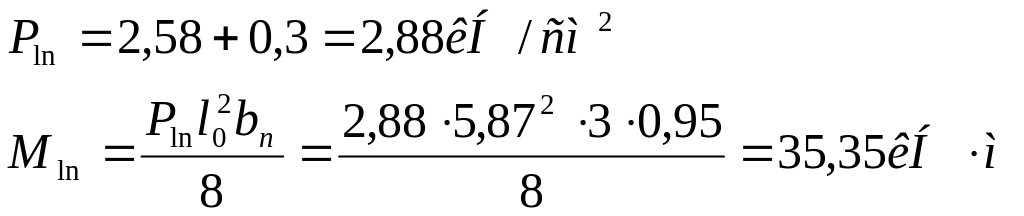
Приращение напряжений в растянутой арматуре от действия полной нагрузки:
,
где
От действия длительной нагрузки:
,
Затем определяется ширина раскрытия трещин от кратковременного действия полной нагрузки:
;
от непродолжительного действия длительной нагрузки:
,
где
;
;
- диаметр напрягаемой арматуры, мм.
Ширина раскрытия трещин от постоянной и временной длительной нагрузки:
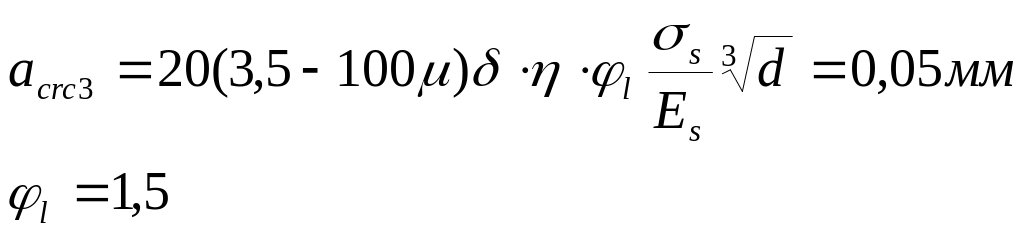
где
Непродолжительная ширина раскрытия трещин:
мм
Долговременная ширина раскрытия трещин:
мм