
- •Тема. Визначений інтеграл
- •1. Обчислення визначених інтегралів за формулою Ньютона – Лейбніца.
- •2. Заміна змінної в визначених інтегралах.
- •3. Інтегрування визначеного інтеграла по частинах.
- •Іv. Невласні інтеграли.
- •V. Наближені обчислення визначеного інтеграла.
- •VI. Теорема про середнє значення.
- •Приклади типових задач.
Приклади типових задач.
Приклад 1.
Обчислити
 .
.
Розв’язання.

![]() .
.
Приклад 2.
Обчислити інтеграл
![]() .
.
Розв’язання.
![]()
![]()
![]() .
.
Приклад 3.
Обчислити
інтеграл
![]() .
.
Розв’язання.


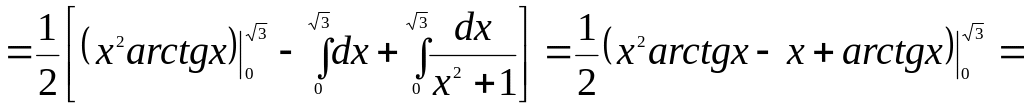
 .
.
Приклад 4.
Обчислити площу фігури, обмеженої
заданими параболами
![]()
Розв’язання.
Знайдемо абсциси точок перетину заданих парабол. Для цього прирівняємо праві частини цих рівнянь:
![]()
Звідси
![]()
![]()
П
Рис. 2.2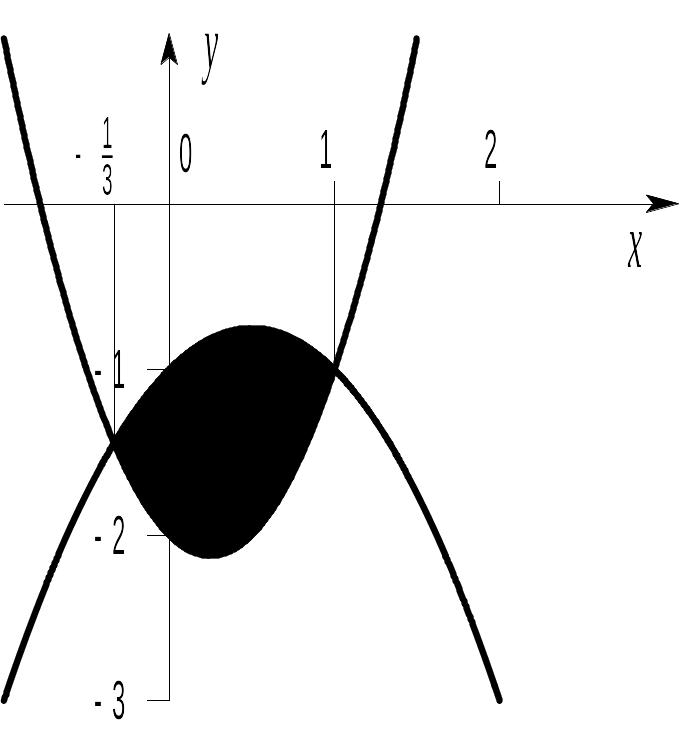
![]()
де
![]() – криві, які обмежують фігуру
– криві, які обмежують фігуру
![]() .
.
В нашому випадку маємо
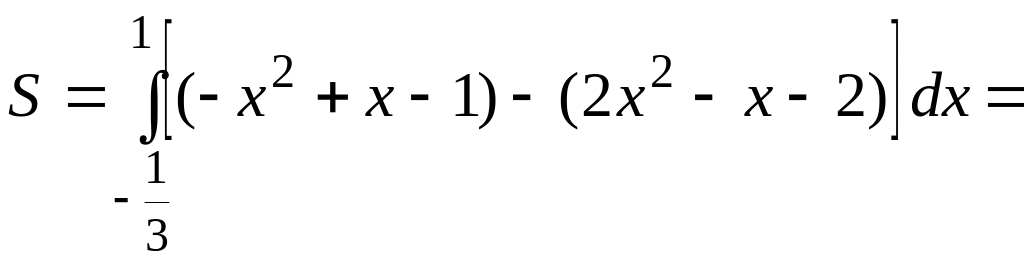

1. Користуючись формулою Ньютона – Лейбніца, обчислити визначені інтеграли:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
![]() .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
7.
.
7.
![]() .
.
8.
![]() . 9.
. 9.
![]() .
10.
.
10.
![]() .
11.
.
11.
![]() .
.
2. Користуючись правилом заміни змінної, обчислити визначені інтеграли:
1.
![]() .
2.
.
2.
![]() .
3.
.
3.
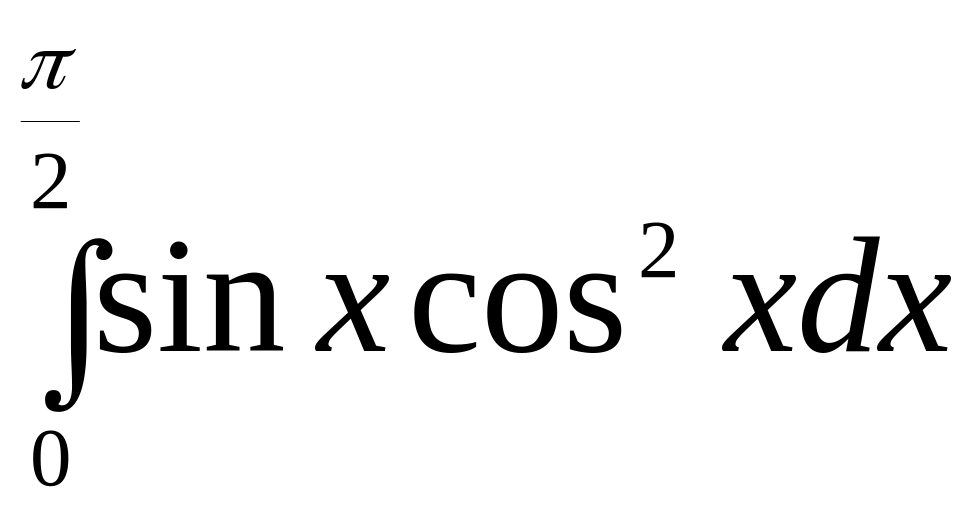 .
4.
.
4.
![]() .
.
5.
![]() .
6.
.
6.
![]() .
7.
.
7.
![]() .
8.
.
8.
![]() .
.
9.
![]() .
10.
.
10.
![]() .
11.
.
11.
![]() .
12.
.
12.
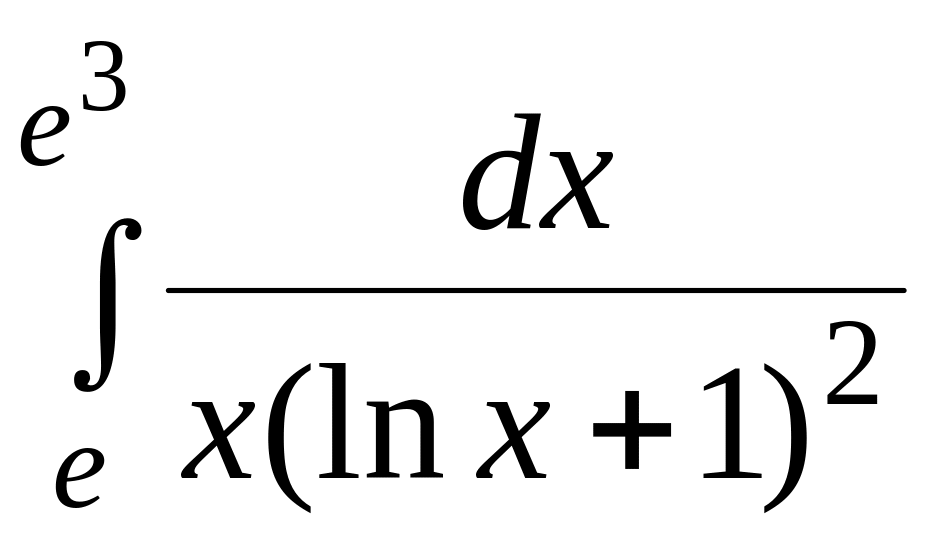 .
.
3. Користуючись правилом інтегрування частинами, обчислити визначені інтеграли:
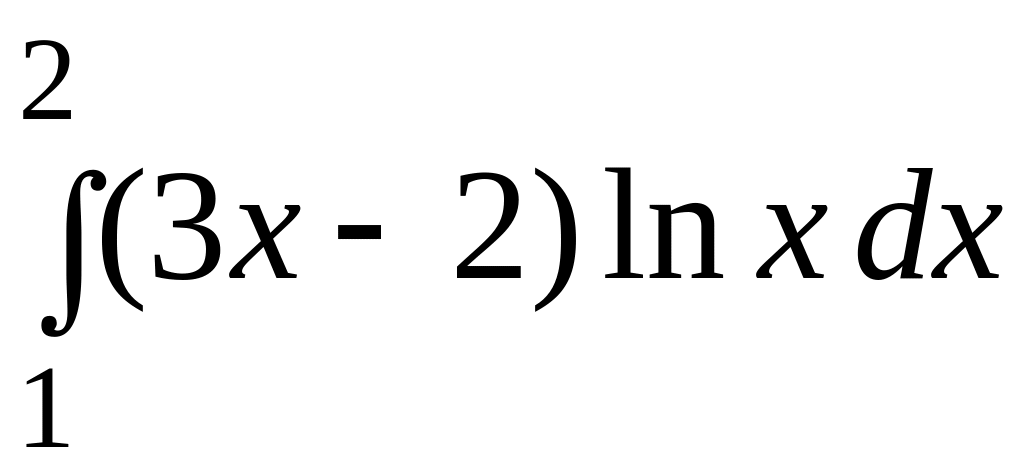 .
2.
.
2.
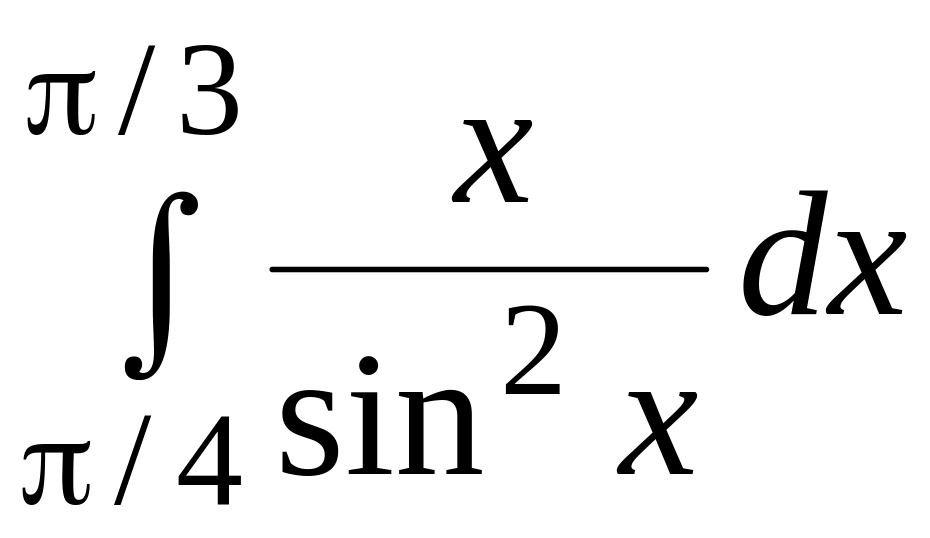 .
3.
.
3.
 .
4.
.
4.
 .
.
5.
![]() .
6.
.
6.
![]() .
7.
.
7.
![]() .
8.
.
8.
![]() .
.
4. Знайти площу фігури, обмеженої вказаними лініями.
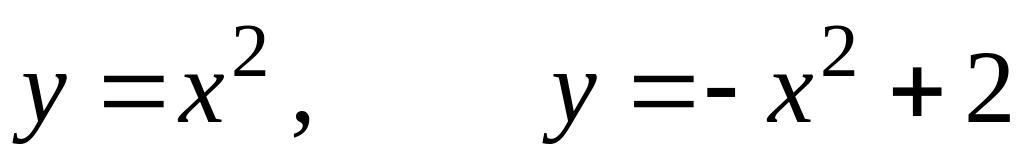 .
. .
. .
. .
. .
. .
.
5. Дослідіть на збіжність невласні інтеграли і, якщо вони збіжні, обчисліть їх.
1.![]() ;
2.
;
2.![]() ;
3.
;
3.![]() ;
4.
;
4.![]() ;
5.
;
5.![]() ;6.
;6.![]() ;
;
7.![]() ;
8.
;
8.![]() ;
9.
;
9.![]() ;
10.
;
10.![]() ;
11.
;
11.![]() ;
12.
;
12.![]() ;
;
13.![]() ;
14.
;
14.![]() ;
15.
;
15.![]() ;
16.
;
16.![]() ;
17.
;
17.
![]() .
.
6. Обчисліть площу фігури, обмежену графіками.
1.![]() ,
,
![]() ;
2.
;
2.![]() ,
,
![]() ;
3.
;
3.![]() ,
,
![]() ;
;
4.
,
![]() ;
5.
;
5.![]() ,
,
![]() ;
6.
;
6.![]() ,
,
![]() ,
,
![]() ;
;
7.![]() ;
;
![]() ;
8.
;
8.![]() ,
,
![]() ,
,
![]() [0;π];
[0;π];
9.![]() ,
,
![]() ;
10.
;
10.![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]() 17.
17.
![]()
