3.5 Линеаризация системы управления. Синтез системы управления, ограничение координат.

Основываясь на полученной ранее линеаризованной структурной схеме объекта управления, составим структурную схему синтезируемой САУ. Система будет содержать два канала х, на входе которого действует управление u_x, и канала у со входным сигналом u_у. Наличие двух каналов управления объясняется тем, что управляемыми величинами объекта управления являются напряжения управления по осям х и у. Поэтому для реализации системы необходимо выполнить синтез двух каналов САУ – канала регулирования потокосцепления ротора, который представляет собой отдельный независимый контур и канала регулирования положения. Структурную схему синтезируемой системы представим на рисунке 3.5.1:

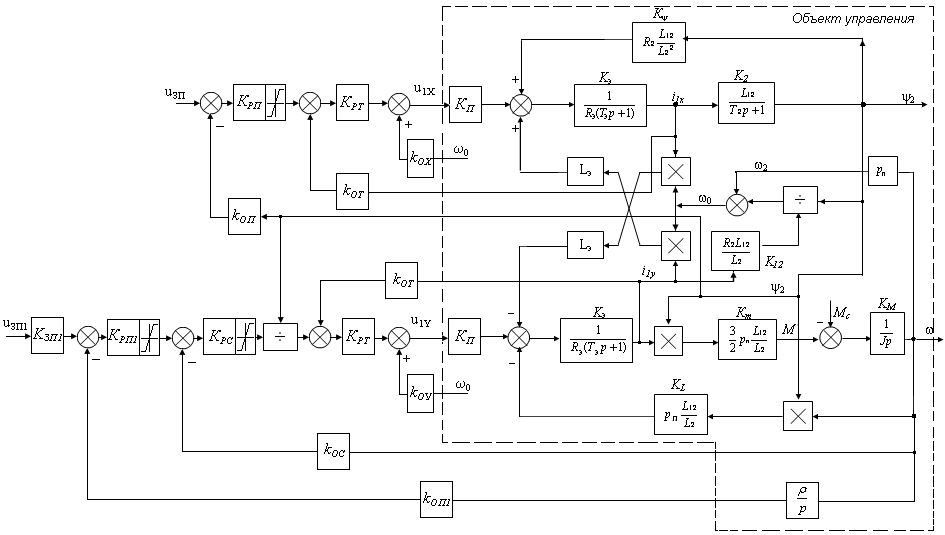
Рис.3.5.1 – Структура векторного управления асинхронным электродвигателем

Все параметры объекта управления уже были определены ранее. На рисунке 3.5.1 к объекту управления также отнесены звенья преобразователя. Передаточную функцию преобразователя можно приближенно представить инерционным звеном.

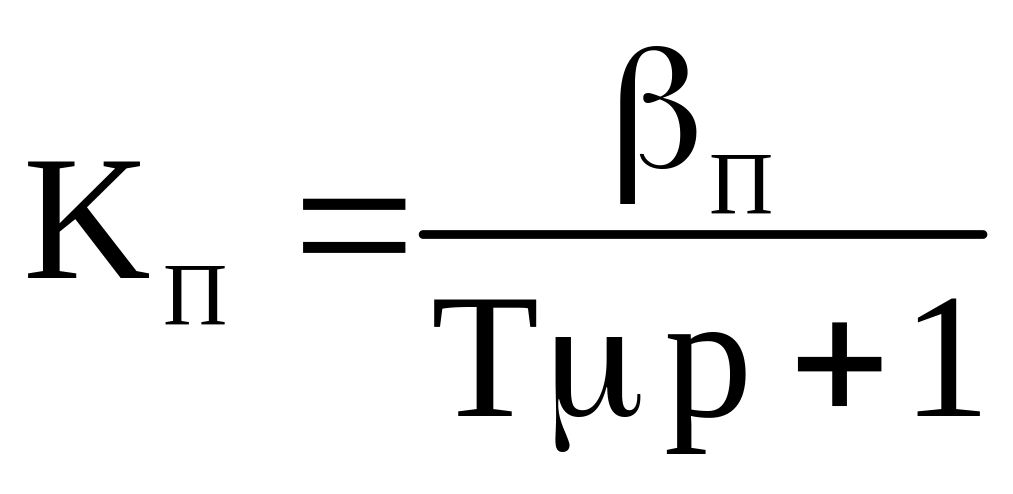(3.5.1)

Так как в настоящее время наиболее применимы автономные инверторы на базе транзисторных силовых ключей обладающих высоким быстродействием, то постоянную времени преобразователя можно принять равной малой некомпенсированной постоянной времени T_μ=0,001c. Коэффициент усиления преобразователя определяется как отношение наибольших значений амплитуды напряжения преобразователя и амплитуды сигнала управления:

Синтез системы начинаем с синтеза первого канала, канала регулирования потокосцепления ротора. Данный канал содержит два контура: контур регулирования тока и контур регулирования потокосцепления. Считая что система стабилизации статическая, передаточные функции всех данных регуляторов будем определять методом последовательной оптимизации контуров на основании условия модульного оптимума. Согласно методике синтеза методом последовательной оптимизации контуров. Обратными внутренними связями объекта управления по потокосцеплению и току пренебрегаем, а все малые постоянные времени датчиков и преобразователя будем считать примерно равными малой некомпенсированной постоянной времени T_μ=0,001c.

Учитывая все вышеперечисленные допущения, получаем замкнутый контур тока в виде представленном на рисунке 3.5.2:

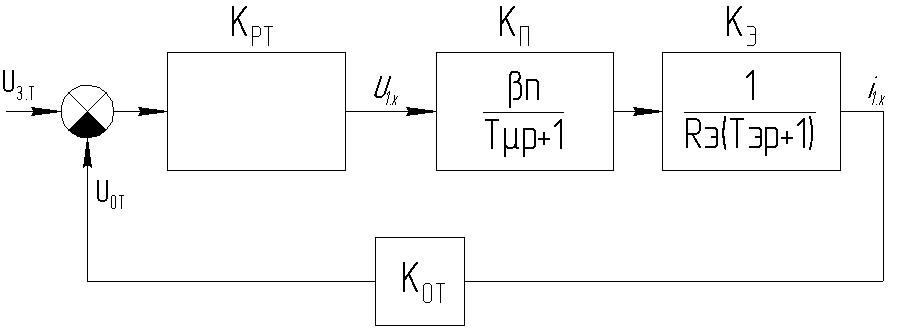
Рисунок 3.5.2 – Замкнутый контур тока.

Записываем уравнение разомкнутого контура тока и приравнивая полученную передаточную функцию к желаемой находим передаточную функцию регулятора тока. Получаем:

(3.5.2)

В замкнутый контур кроме регулятора тока входят два звена, следовательно, порядок контура n=2, по таблице 7.2 [6] для n=2 и из условия настройки на модульный оптимум (МО) выписываем выражение для желаемой передаточной функции разомкнутого контура:

(3.5.2)

Из (3.5.2) выражаем :

(3.5.3)

Подставляя в (3.5.3) выражения для уже известных передаточных функций , и получаем:

(3.5.4)

Вычисляем:

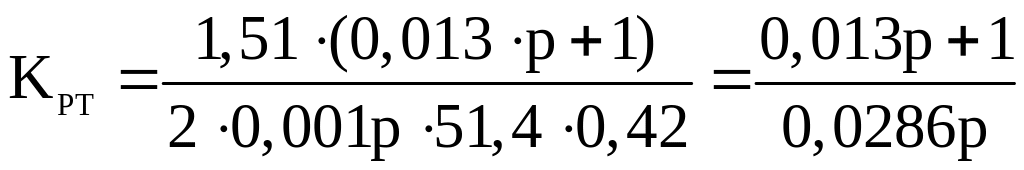(3.5.5)

Передаточная функция для замкнутого контура тока определяется из соотношения:

(3.5.6)

(3.5.7)

Аналогично для контура потокосцепления получаем следующий вид замкнутого контура:

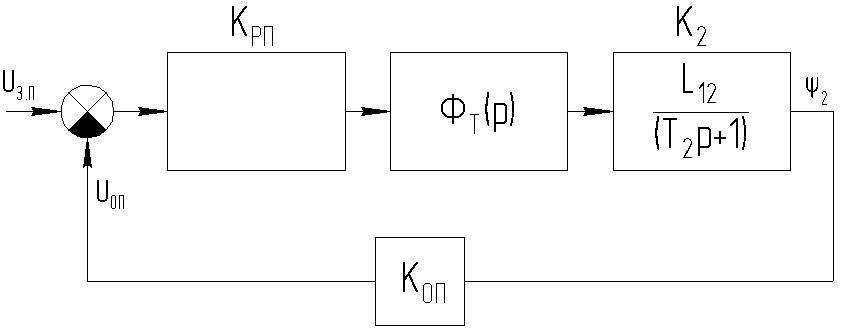
Рисунок 3.5.3 – Замкнутый контур потокосцепления.

Контур регулирования потокосцепления также настраиваем на модульный оптимум (n=3), по таблице 7.2 [6] определяем вид желаемой передаточной функции для разомкнутого контура и записываем уравнение разомкнутого контура:

(3.5.8)

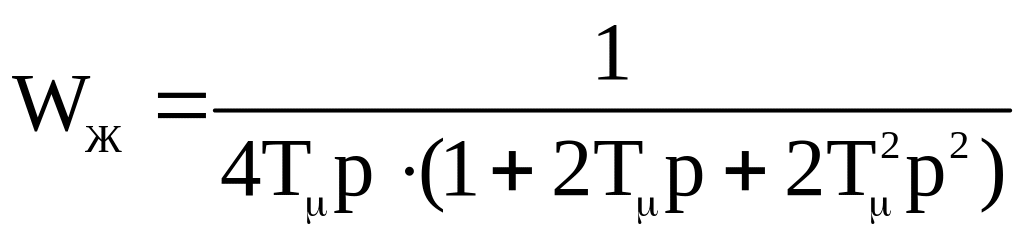(3.5.9)

Из выражений (3.5.9), (3.5.8) выражаем , после всех подстановок получаем:

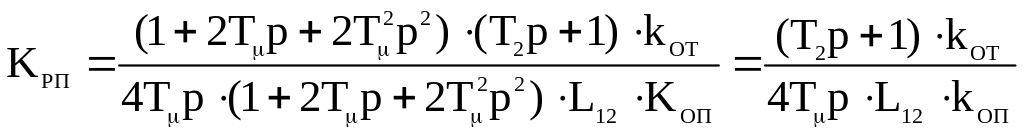(3.5.10)

Вычислим:

(3.5.11)

При условии синтеза регулятора тока контура у также на модульный оптимум выражение передаточной функции будет таким же, как и для контура х. Следовательно, передаточная функция регулятора тока для контура у имеет вид:

(3.5.12)

Синтез контура скорости на модульный оптимум выполняем аналогично. Замкнутый контур регулирования скорости имеет вид:

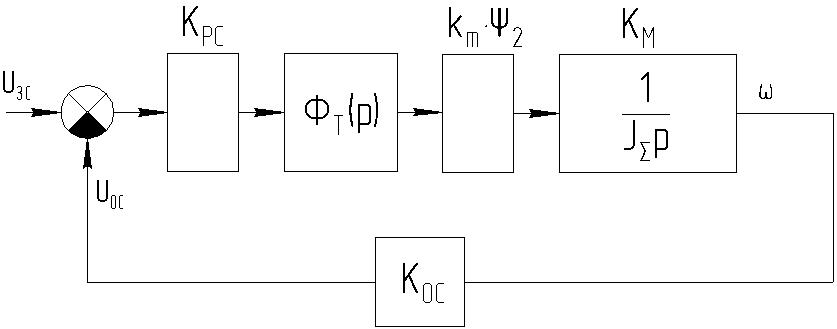
Рисунок 3.5.3 – Замкнутый контур скорости.

Записываем уравнение для разомкнутого контура:

(3.5.13)

Контур регулирования скорости первоначально настраиваем на МО (n=3), по таблице 7.2 [6] определяем вид желаемой передаточной функции для разомкнутого контура:

(3.5.14)

Из (3.5.14) выражаем :

(3.5.15)

Так как значение потокосцепления ротора является переменной величиной, то в структуре вводится блок деления на , как было уже показано на рисунке 3.5.1 С учетом этого получаем:

(3.5.16)

Для обеспечения требуемой точности в установившемся режиме может оказаться необходимостью реализовать контур скорости в виде пропорционально-интегрирующего звена (ПИ – регулятор вместо П). В этом случае порядок системы повышается, а синтез контура скорости выполняется по условиям симметричного оптимума (СО). Выполним синтез контура скорости на СО. Вид желаемой передаточной функции разомкнутого контура из таблицы 7.2 [6] при настройке на СО (n=4) имеет вид:

(3.5.17)

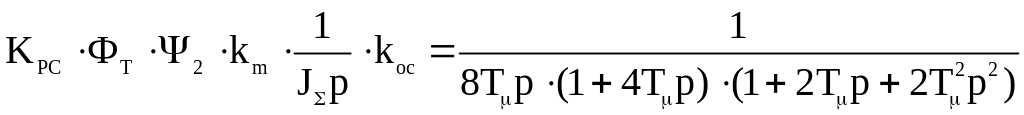
Получаем передаточную функцию контура скорости при настройке на симметричный оптимум в виде:

(3.5.18)

(3.5.19)

Синтез контура регулирования положения выполняется по условию настройки на МО не зависимо от настройки контура скорости. Необходимо только отметить, что при настройке контура скорости на СО, в контуре тока, настроенном на МО, необходимо использовать фильтр.

Выполним расчет контура регулирования положения при его настройке на модульный оптимум. Получаем следующий вид замкнутого контура, который представим на рисунке 3.5.4:

Рисунок 3.5.3 – Замкнутый контур положения.

(3.5.20)

Желаемая передаточная функция разомкнутого контура при настройке на МО и n=4:

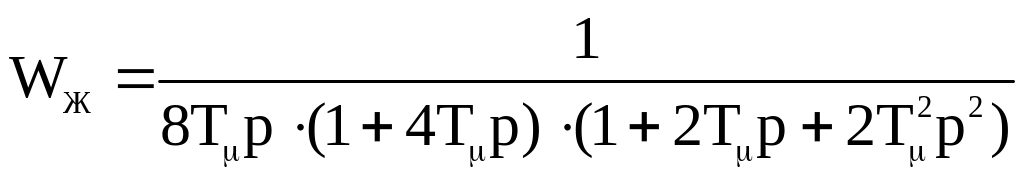(3.5.21)

Передаточная функция замкнутого контура скорости синтезированного на модульный оптимум:

(3.5.22)

Получаем следующее значение коэффициента усиления регулятора положения :

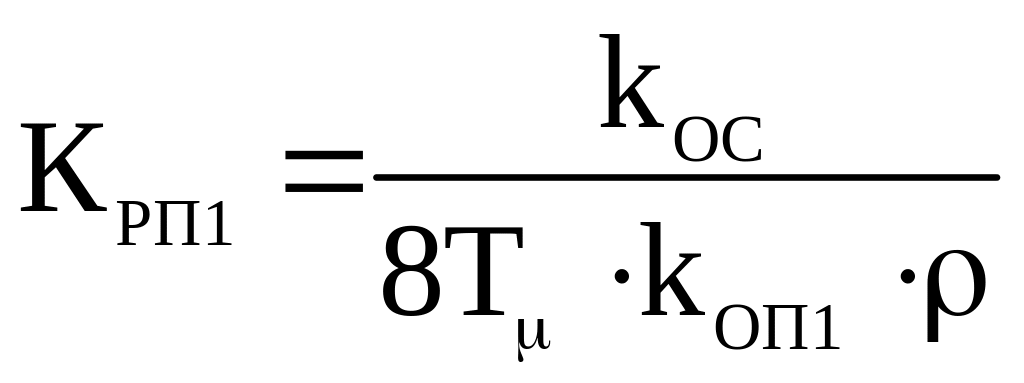(3.5.23)

Вычисляем:

(3.5.24)

Если контур скорости был синтезирован на симметричный оптимум, то передаточная функция регулятора положения изменится и будет ровна:

(3.5.25)

Для устранения перерегулирования по положению, повышения точности отработки заданного перемещения и обеспечения качества переходных процессов используем в системе комбинированный регулятор положения, который представляет собой регулятор положения с переменной структурой. Использование регулятора положения такого типа позволяет системе правильно и с высокой точностью отрабатывать не только малые, но также средние и большие перемещения.

В общем случае регулятор положения будет работать в соответствии с уравнениями:

(3.5.26)

где .

.

С учетом этого получаем:

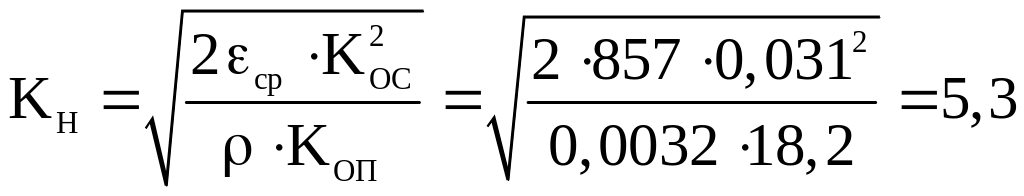(3.5.27)

Величина зоны нечувствительности:

Точка сопряжения характеристик:

Смещение:

На линейном участке характеристики коэффициент усиления преобразователя будет равен уже рассчитанному ранее значению:

.

Ограничения регуляторов выполняем на уровне ± 10В.

Практически, ограничения выходных величины регуляторов выполним с помощью нелинейных элементов – стабилитронов, включаемых в цепь обратной связи операционных усилителей.