Іі. Практична частина

Завдання 1 На основі наведених нижче даних соціологічного опитування 500 сімей оцінити щільність зв’язку між доходами сім’ї та кількістю дітей у сім’ї:

Дохід	Кількість дітей
	Немає дітей	Одна дитина	Дві дитини	Більше двох дітей
Нижче і на рівні прожиткового мінімуму	16	152	64	18
Вище прожиткового мінімуму	7	144	96	3

Завдання 2 Є наступні дані про розподіл робітників за стажем і кваліфікаційним розрядом:

Розряд	Стаж роботи, років
	До 10	10 і понад
1-3	70	30
3-6	10	60

Обчислити коефіцієнт асоціації і зробити висновок.

Завдання 3Дані отримані за тестом наведені в таблиці. Знайти коефіцієнт кореляції Пірсона.

Об’єкт	Ознака X	Ознака Y
1 2 3 4 5 6 7 8 9 10 11 12	1 1 0 1 0 0 0 1 0 1 0 0	0 0 1 1 1 0 1 0 1 1 0 1

Запитання для самоконтролю

1. Яка відмінність між функціональним і статистичним зв’язком?

2. Що характеризує коефіцієнт кореляції?

3. В яких випадках використовують непараметричні методи оцінки зв’язку?

4. В яких межах знаходяться значення коефіцієнтів Чупрова та Пірсона?

ПРАКТИЧНЕ ЗАНЯТТЯ №5. ОБЧИСЛЕННЯ КОЕФІЦІЄНТІВ РАНГОВОЇ КОРЕЛЯЦІЇ СПІРМЕНА, КЕНДАЛА ТА КОЕФІЦІЄНТА КОНКОРДАЦІЇ W.

І. Теоретична частина

10. Коефіцієнти рангової кореляції Спірмена, Кендала.

11. Коефіцієнт конкордації W.

Методичні рекомендації до виконання завдань

1. Якщо декілька ознак мають однакову кількісну характеристику, то ми маємо справу із зв’язаними рангами, у цьому випадку ранг всих цих ознак дорівнює середньому арифметичному їхніх порядкових місць. Коефіцієнт Спірмена використовується для встановлення кореляційної залежності, коли досліджується довільна кількість об’єктів по двом ознакам, що проранжовані по зростанню (спаданню)та обчислюється за формулою:

, де - об’єм вибірки, - ранг і-того об’єкта по ознаці Х, - ранг і-того об’єкта по ознаці У.

2. У випадку коли в досліджуваній ознаці є зв’язані ранги працює також коефіцієнт Кендала. Він базується на числі співпадань та інверсій в ранжуванні досліджуваних ознак Х та У.

Алгоритм обчислення коефіцієнта Кендала:

1. Значення ознаки Х ранжуються в порядку зростання чи спадання;

2. Значення ознаки У розміщуються відповідно до значень ознаки Х;

3. Для кожного рангу ознаки У визначається число слідуючих за ним рангів, які перевищують даний ранг. Просумувавши ці числа обчислюють величину Р- величину співпадань.

4. Для кожного рангу ознаки У визначається число слідуючих за ним рангів, які менші від даного рангу. Просумувавши ці числа обчислюють величину Q- величину інверсій.

5. Обчислюємо безпосередньо коефіцієнт Кендала за формулою

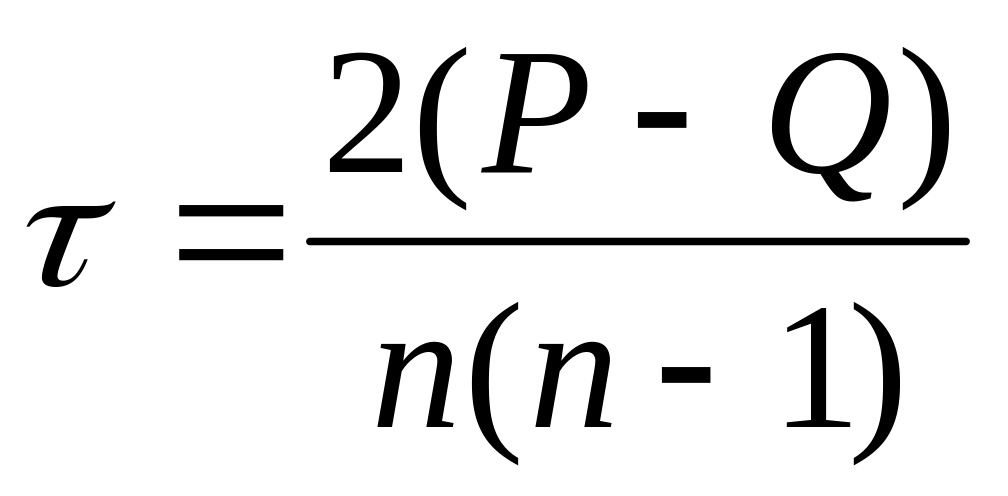
Коефіцієнти та зв’язані , якщо вибірка достатньо велика.

3. Для встановлення зв’язка між довільним числом проранжованих ознак використовують коефіцієнт конкордації W, що обчислюється за формулою:

, де k –число ознак змінних, N – число об’єктів що ранжуються, S –відхилення суми квадратів рангів від середнього значення квадрата суми рангів , a- сума рангів.

Приклади розв’язування типових задач

Приклад 1. В таблиці проранжовано 8 студентів по ознакам Х – гарне ставлення до навчання та У – гарне ставлення до викладача. Причому рагн 1 надається тому студенту, який виявляє найкраще відношення. Встановіть кореляційну залежність між знаками Х та У.

Об’єкт	1	2	3	4	5	6	7	8
Х	2	3	4	1	6	5	7	8
У	1	2	5	3	8	7	4	6

Розв’язання: перед застосуванням формули здійснимо проміжні розрахунки, використовуючи для зручності таблицю:

Об’єкт	Х	У	хі-уі	(хі-уі)2
1	2	1	1	1
2	3	2	1	1
3	4	5	-1	1
4	1	3	-2	4
5	6	8	-2	4
6	5	7	-2	4
7	7	4	3	9
8	8	6	2	4
Сума:				28

Висновок: кореляційна залежність існує і досить сильна.

Приклад 2. Обчислити коефіцієнт кореляції Кендала для даної таблиці

Об’єкт	1	2		3			4	5	6		7		8	9		10
Х	1	4		2			3	7	5		6		8	9		10
У	3	1		2			4	5	6		8		9	7		10

Об’єкт	Х	У	Х - ранг	У - ранг	Р	Q
1	1	3	1	3	7	2
2	4	1	2	2	7	1
3	2	2	3	4	6	1
4	3	4	4	1	6	0
5	7	5	5	6	4	1
6	5	6	6	8	2	2
7	6	8	7	5	3	0
8	8	9	8	9	1	1
9	9	7	9	7	1	0
10	10	10	10	10	0	0
Сума:					37	8

Розв’язання: перед застосуванням формули здійснимо проміжні розрахунки, використовуючи для зручності таблицю:

Висновок: кореляційна залежність існує і досить сильна.

Об’єкт	Ранги ознак
	A	B	C
№1	3	1	1
№2	1	2	3
№3	2	6	5
№4	4	3	2
№5	5	4	4
№6	6	5	6

Приклад 3. Обчислити коефіцієнт конкордації для даної таблиці

Розв’язання: перед застосуванням формули здійснимо проміжні розрахунки, використовуючи для зручності таблицю:

Об’єкт	Ранги ознак			∑ рангів у рядках, a	Квадрат суми
	A	B	C
№1	3	1	1	5	25
№2	1	2	3	6	36
№3	2	6	5	13	169
№4	4	3	2	9	81
№5	5	4	4	13	169
№6	6	5	6	17	289
				63	769

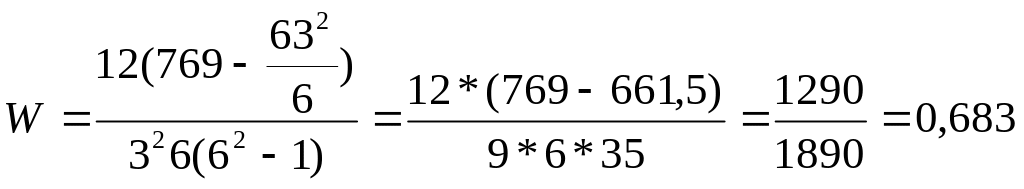
Висновок: кореляційна залежність існує і досить сильна.