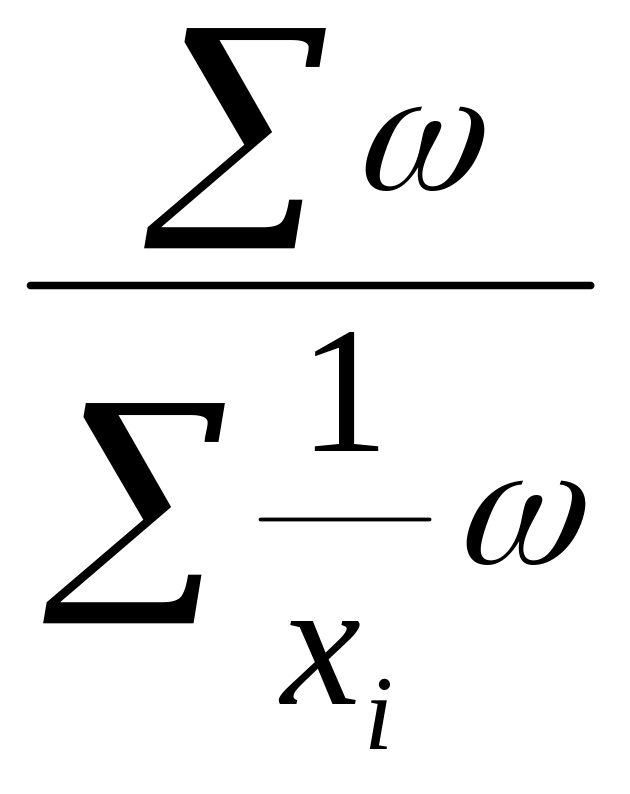ПЛАНИ ПРАКТИЧНИХ ЗАНЯТЬ З НАВЧАЛЬНОЇ ДИСЦИПЛІНИ

«мАТЕМАТИЧНІ МЕТОДИ У ПЕДАГОГІЧНИХ ДОСЛІДЖЕННЯХ»

ТЕМИ №2 - 3: Описова статистика. Міри центральної тенденції, ВаРІАЦІЇ, Особливості їх використанняи та їх інтерПРЕТАЦІЯ У ПЕДАГОГіЧНОМУ ЕКСПЕРИМЕНТІ

ПРактичне ЗАНЯТТЯ№1-2

І. ТЕОРЕТИЧНА ЧАСТИНА

1. Вимірювання в соціально-педагогічних дослідженнях. Основні вимірювальні шкали.

2. Ряди розподілу: дискретні та варіаційні ряди.

3. Обчислення моди, медіани.

4. Обчислення середніх величин: середньої арифметичної, геометричної, гармонійної, квадратичної.

5. Дисперсія. Асиметрія. Ексцес. Коефіцієнт варіації.

основнІ понятТЯ та МЕТОДИЧНІ РЕКОМЕНДАЦІЇ до виконання завдань

Застосування математичних методів до педагогічного експерименту передбачає дослідження генеральної су­купності статистично, тобто виявлення властивостей генеральної сукупності за вибіркою. Для наочності, за вибіркою складають статистичний ряд. Це таб­лиця, в першому рядочку якої записані у зростаючому порядку різні варіанти зна­чень вибірки х_{і ,} а в другому – частоти n_i появи цих значень у вибірці.

Якщо кількість різних варіант дуже велика, то дані групують: складають інтервальний варіаційний ряд. Для цього інтервал значень варіаційного ряду (х_min; x_max) розбивають на інтервали однакової довжини, яку визначають за фор­мулою Стерджеса

Початок першого інтервалу знаходять за формулою .

Графіки варіаційних рядів. Використовують два види графіків: полігон і гіс­то­граму. Полігон будують для середин інтервалів або для статистичних рядів, гіс­­то­граму - для інтервалів. При побудові полігона по вісі OY відкладають час­то­ти появи відповідних значень, а по вісі OX - середини інтервалів або значен­ня ва­рі­ант статистичного ряду. При побудові гістограми по вісі OY відкладають зна­чен­ня , де - частота появи кожного інтервалу, - об’єм вибірки, - ве­­ли­чи­на інтервалу, а по вісі OX - інтервали.

Числові характеристики статистичного розподілу

Мода– це значення, яке в статистичному ряді зустрічається найчастіше (М₀).

Правило обчислення моди: якщо всі значення в ряді зустрічаються однакову кількість разів, то у цей ряд моди не має; якщо два сусідні значення зустрічаються однакову кількість разів, то мода дорівнює їх середньому арифметичному; якщо два несусідні значення зустрічаються однакову кількість разів, то ряд має дві моди і називається бімодальним

Для інтервального варіаційного ряду розподілу з однаковими інтервалами моду обчислюють за формулою Орженцького: , де - нижня межа модального інтервалу, - частоти перед модального, модального, після модального інтервалу . - довжина інтервалу.

Медіана – це значення, яке займає центральне місце у впорядкованому ряді розподілу (М_е).Правило обчислення медіани: для дискретного впорядкованого варіаційного ряду

З непарним числом елементів медіану знаходять як варіант х з порядковим номером (n+1)/2 : . Для ряду з парним числом елементів медіану розраховують як середню арифметичну двох варіантів з номерами та : 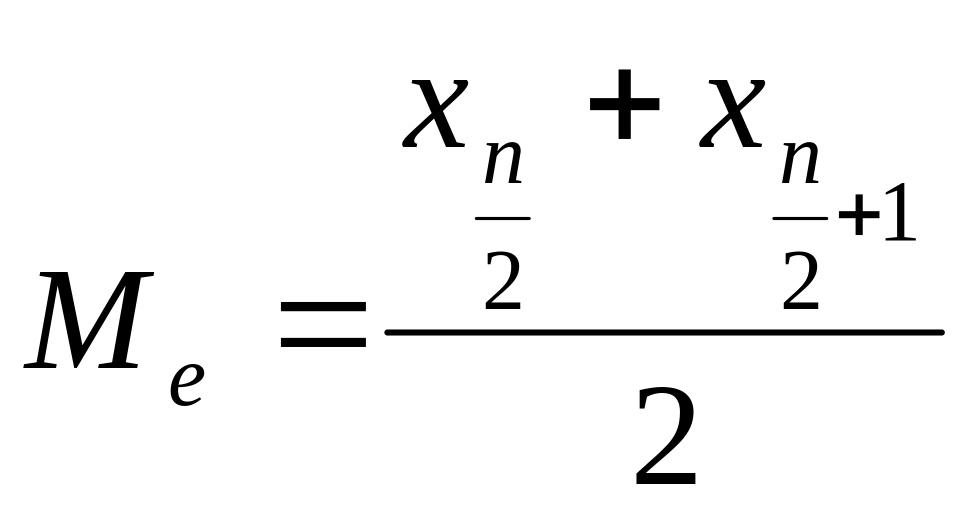, для інтервального ряду розподілу: , де - нижня межа медіанного інтервалу, - довжина медіанного інтервалу, - сума частот нагромаджених перед медіанним інтервалом, - половина суми частот, .

Примітка: медіанний інтервал визначається як інтервал для якого нагромаджена частота дорівнює півсумі всіх частот ряду, або перевищує її.

Середнє арифметичне – займає центральне місце в ряді і характеризує середнє значення певної ознаки ( )

Середня гармонійна є величиною, яка обернена до середньої арифметичної з обернених значень ознаки ( )

Середня геометрична – значення, яке займає центральне місце у виборці, що являє собою геометричну прогресію ( ).

Середнє квадратичне використовують при розрахунках абсолютних і відносних показників варіації ( )

Розрахунок середніх величин

Види середньої	Розрахункова формула середньої
	простої	зваженої
Середня арифметична,
Середня гармонійна,
Середня геометрична,
Середнє квадратичне,

У розрахункових формулах прийняті такі позначення: - значення ознаки; - частота появи значення ознаки; - обсяг сукупності; - обсяг значення ознаки ( )

Дисперсія – міра розсіювання, що дорівнює середньому значенню квадрата відхилень окремих значень від середнього арифметичного. Обчислюється за формулою:

Середнє квадратичне відхилення – міра розсіювання, яка показує наскільки в середньому кожне значення ряду відхиляється від середнього арифметичного. Обчислюється за формулою:

Асиметрія – кількісна міра стрімкості нахилу симетричного розподілу. Обчислюється за формулою: , область значень - + ,якщо 0 , то розподіл має нахил вліво, 0 – нахил вправо, =0 – розподіл симетричний.

Ексцес – кількісна міра випуклості (пологості) верхньої частини кривої розподілу. Обчислюється за формулою: . Область значень - +

Коефіцієнт варіації – міра відношення середньоквадратичного відхилення до середнього арифметичного вираженого у відсотках. Обчислюється за формулою: .

Вибіркові числові характеристики (для інтервальних варіаційних рядів)

• Вибіркове середнє

• Вибіркова дисперсія

• Виправлена вибіркова дисперсія

• Середнє квадратичне відхилення

• Вибірковий коефіцієнт асиметрії

, де - центральний момент ІІІ порядку, S – середнє квадратичне відхилення.

• Вибірковий коефіцієнт ексцеса

, де - центральний момент ІV порядку, S – середнє квадратичне відхилення.