
- •Основні теореми диференціального числення.
- •Приклади
- •Завдання для самостійного розв’язування
- •§4.4. Застосування похідної до дослідження функцій
- •Алгоритм знаходження інтервалів зростання і спадання,
- •Алгоритм знаходження інтервалів опуклості вгору,
- •Приклади
- •Завдання для самостійного розв’язування
Основні теореми диференціального числення.
Правило Лопіталя
Якщо функція y=f(x)
неперервна на відрізку [a;b],
диференційовна на інтервалі (a;b),
причому f(а)=f(b),
то існує принаймні одна точка с(a;b)
така, що
 (теорема
Ролля).
(теорема
Ролля).
Г еометричний
зміст теореми Ролля.
Якщо функція задовольняє умови теореми
Ролля, то серед усіх дотичних до кривої
y=f(x)
існує принаймні одна, паралельна осі
Ох (рис.4.2).
еометричний
зміст теореми Ролля.
Якщо функція задовольняє умови теореми
Ролля, то серед усіх дотичних до кривої
y=f(x)
існує принаймні одна, паралельна осі
Ох (рис.4.2).
Якщо функції y=f(x)
і y=(x)
неперервні на відрізку [a;b]
і диференційовні на інтервалі (a;b),
причому
 ,
то існує принаймні одна точка с(a;b)
така, що
,
то існує принаймні одна точка с(a;b)
така, що
 (теорема
Коші).
(теорема
Коші).
Якщо в умові теореми Коші розглянути функцію (x)=х, то буде справедливе наступне твердження.
Якщо функція y=f(x) неперервна на відрізку [a;b] і диференційовна на інтервалі (a;b), то існує принаймні одна точка с(a;b) така, що
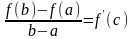
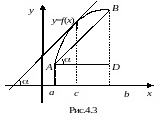 (теорема
Лагранжа).
(теорема
Лагранжа).
Геометричний
зміст теореми Лагранжа.
Якщо функція y=f(x)
задовольняє умови теореми Лагранжа, то
серед усіх дотичних до кривої y=f(x)
знайдеться принаймні одна, яка паралельна
хорді АВ,
де
 ,
,
 (рис.4.3). І дійсно,
(рис.4.3). І дійсно,
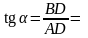
 ,
,
 .
.
Для розкриття
невизначеностей вигляду
 і
і
 використовують правило
Лопіталя.
Нехай функції f
і g
диференційовні в деякому околі точки
х0
(скінченої або нескінченно віддаленої),
крім, можливо, безпосередньо точки х0.
Якщо f
і g
при хх0
є одночасно
нескінченно малими
використовують правило
Лопіталя.
Нехай функції f
і g
диференційовні в деякому околі точки
х0
(скінченої або нескінченно віддаленої),
крім, можливо, безпосередньо точки х0.
Якщо f
і g
при хх0
є одночасно
нескінченно малими
 або нескінченно великими
або нескінченно великими
 ,
причому існує границя
,
причому існує границя
 ,
то існує також границя
,
то існує також границя
 і має місце рівність
і має місце рівність
= . (4.11)
Якщо не існує, то правило Лопіталя застосовувати не можна, хоча шукана границя може існувати.
Правило Лопіталя можна застосовувати декілька разів.
Крім розглянутих невизначеностей, зустрічаються ще такі:
0, +–(+), 00, 0, 1.
Кожну з цих невизначеностей можна звести до невизначеності або за допомогою таких перетворень:
0=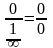 або 0=
або 0= ,
,
+–(+)= ;
;
00=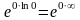 ;
0=
;
0= ;
1=
;
1=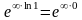 .
.
Приклади
Використовуючи правило Лопіталя, знайти границі:
а)
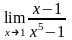 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
г)
 ;
д)
;
д)
 ; е)
; е)
 .
.
Розв’язання. а) Маємо невизначеність вигляду . Використовуючи правло Лопіталя (формулу (4.11)), одержимо:
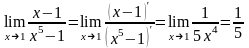 .
.
б) Також маємо невизначеність вигляду . Використовуючи правло Лопіталя тричі, одержимо:
 .
.
в) Маємо невизначеність вигляду . Розкриваючи її за правилом Лопіталя, одержимо:
 .
.
г) Маємо невизначеність вигляду 0. Зведемо її до невизначеності вигляду , а потім використаємо правило Лопіталя:
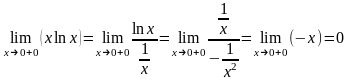 .
.
д) Маємо невизначеність вигляду –. Зведемо її до невизначеності вигляду , а потім використаємо правило Лопіталя:
=
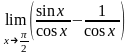 =
= =
= =
=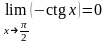 .
.
е) Маємо невизначеність вигляду 1.
=
 .
.
Знайдемо
 .
Маємо невизначеність вигляду 0.
Зведемо її до невизначеності вигляду
,
а потім використаємо правило Лопіталя
та границю
.
Маємо невизначеність вигляду 0.
Зведемо її до невизначеності вигляду
,
а потім використаємо правило Лопіталя
та границю
 :
:
= =
=
=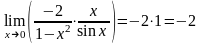 .
.
Отже,
= .
.
Завдання для самостійного розв’язування
1. Використовуючи правило Лопіталя, знайти границі:
1)
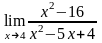 ;
2)
;
2)
 ;
3)
;
3)
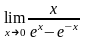 ;
4)
;
4)
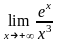 ;
;
5)
 ;
6)
;
6)
 ;
7)
;
7)
 .
.
Відповіді:
1.
1)
 ;
2) 2; 3)
;
2) 2; 3)
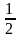 ;
4) +;
5) 0; 6)
;
4) +;
5) 0; 6)
 ;
7)
.
;
7)
.
