3. Закрытая цилиндрическая прямозубая передача

Смещение исходного контура отсутствует. Исходные данные: Р₁ - номинальная передаваемая мощность на валу шестерни, кВт; n₁ - частота вращения шестерни, мин ^-1; u - передаточное число рассчитываемой пары.

3.1. Выбираем материал и термообработку, определяем допускаемые напряжения для шестерни и колеса _Н МПа, _F МПа (см. разделы 1 и 2).

3.2. Выбираем коэффициент ширины зубчатого колеса относительно межосевого расстояния _bа по табл. 3.1. Определяем коэффициент ширины шестерни относительно ее диаметра

_bd = 0,5 _bа (U1).

Знак "+" для наружного, а "-" для внутреннего зацепления.

3.3. Определяем коэффициент, учитывающий неравномерность распределения нагрузки по ширине зубчатого венца при расчете на контактную выносливость K_H по рис. 3.1 в зависимости от коэффициента _bа, твердости шестерни Н₁ и колеса Н₂. Цифры у кривых соответствуют передачам, указанным на схемах. Консольному расположению зубчатого колеса и валу на шарикоподшипниках соответствует кривая 1, валу на роликоподшипниках –кривая 2.

Если значение _bd лежит вне пределов графика, следует уменьшить _bd, приняв меньшее значение _bа.

Таблица 3.1

Рекомендуемые значения коэффициента _bа.

Положение зубчатых колес относительно опор
Симметричное	Несимметричное	Консольные (одного или обоих колес)
0,315...0,5	0,25...0,4	0,2...0,25

Примечание. Меньшие значения _bа для передач с повышенной твердостью поверхности зубьев HRC > 45. Для каждой последующей ступени передачи редуктора _bа увеличивают на 20...30%. Для передвижных зубчатых колес коробок передач _bа = 0,1...0,2.

К_Н при Н₁НВ 350 или Н₂НВ 350

К_Н при Н₁>НВ 350 и Н₂>НВ 350

Рис. 3.1. График для определения коэффициента K_H

Таблица 3.2

Ряд модулей в наиболее употребительном диапазоне

(следует предпочитать 1-й ряд)

Ряды	Модуль, мм
1-й	1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25
2-й	1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 7; 9; 11; 14; 18; 22

3.4. Определяем межосевое расстояние из условия контактной выносливости зубьев

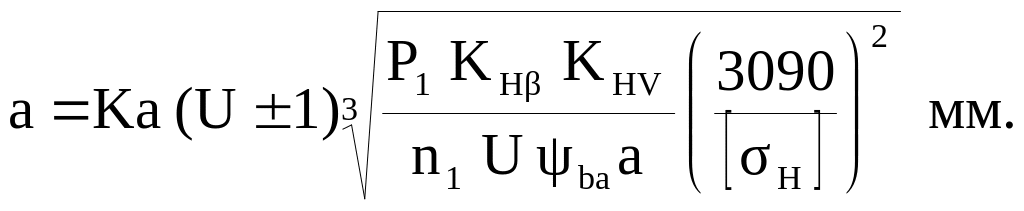
Знак “+” для наружного зацепления, а “-” для внутреннего зацепления. Для стальных колес

Ка = 50 Мпа ^1/3

К_HV – коэффициент динамической нагрузки при расчете на контактную выносливость. Предварительно принимаем К_HV = 1,1.

3.5. Определяем ширину колеса мм

b₂ = _bа  а.

Значение “b” округляем до целого числа. Ширину шестерни рекомендуется принимать на 2...5 мм больше ширины колеса для компенсации неточностей установки в осевом направлении.

3.6. Определяем модуль мм: m = (0,01...0,02)  a.

Величина модуля округляется до стандартного значения из ряда чисел по табл. 3.2. Для силовых передач рекомендуется принимать m1,5 мм.

3.7. Находим число зубьев шестерни

.

Округляем до целого числа. Знак “-” для внутреннего зацепления. Минимально допустимое число зубьев при нарезании инструментом реечного типа

Zmin = 17.

3.8. Определяем число зубьев колеса Z₂ = Z₁U. Округляем до целого числа.

3.9. Уточняем передаточное число передачи Z₂ / Z₁ = U.

3.10. Находим делительные диаметры колес (вычисления производим с точностью до сотых долей диаметра)

d₁ = mZ₁ ; d₂ = mZ₂.

3.11. Уточняем межосевое расстояние передачи

, мм.

Знак “-” для внутреннего зацепления. Значение а вычисляем с точностью до сотых долей миллиметра.

3.12. Находим окружную скорость

м/с.

3.13. Выбираем степень точности передачи (табл. 3.3).

3.14. Определяем окружную силу в зацеплении (Н)

.

3.15. Определяем коэффициент динамической нагрузки при расчете на контактную выносливость К_HV. (см. раздел 6.1).

3.16. Выполняем проверочный расчет зубьев на контактную выносливость

.

Знак “-” для внутреннего зацепления.

Таблица 3.3

Ориентировочные рекомендации по выбору

степени точности передачи

Степень точности не ниже	Окружная скорость, м/с не более		Примечание
	Прямо- зубая	Косо -зубая
6 (высокоточные)	15	25	Высокоскоростные передачи, механизмы точной кинематической связи – делительные, отсчетные и т.п.
7 (точные)	10	17	Передачи при повышенных скоростях и умеренных нагрузках или при повышенных нагрузках и умеренных скоростях.
8 (ср. Точности)	6	10	Передачи общего машиностроения, не требующие особой точности.
9 (пониженной точности)	2	3,5	Тихоходные передачи с пониженными требованиями к точности

Таблица 3.4

Коэффициент Y_F формы зуба зубчатых колес

внешнего зацепления

Число зубьев Z или ZV
17	20	25	30	40	50	60	80	100	150	200
4,25	4,07	3,90	3,79	3,70	3,65	3,62	3,61	3,60	3,60	3,60	3,63

Здесь Z_H = 1,77 - коэффициент, учитывающий форму сопряженных поверхностей зубьев;

Z_М = 175 МПа ^½ (для стальных зубчатых колес) – коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес;

Z_ = 1 - коэффициент, учитывающий суммарную длину контактных линий;

_Ht - удельная расчетная окружная сила при расчете на контактную выносливость

.

Если расчетные напряжения превышают допускаемые в пределах 5%, в перерасчете нет необходимости. При большем превышении можно изменить материал и термообработку, либо увеличить межосевое расстояние.

3.17. Находим коэффициент неравномерности нагрузки при расчете на выносливость по напряжении изгиба K_F по рис. 3.2. Цифры у кривых соответствуют передачам, указанным на схемах рис. 3.1 (см. п. 3.3).

3.18. Определяем коэффициент динамической нагрузки при расчете на выносливость по напряжению изгиба K_FV – см. Раздел 6.2.

К_F при Н₁НВ 350 или Н₂НВ 350

К_F при Н₁>НВ 350 и Н₂>НВ 350

Рис. 3.2. График для определения коэффициента K_F

3.19. Выполняем проверочный расчет зубьев на выносливость по напряжению изгиба (МПа)

,

где У_F – коэффициент формы зуба, для колес внешнего зацепления; определяется по табл. 3.4.

Для колес с внутренними зубьями

.

Для шестерни и колеса определяем значения _F₁/У_F1, и _F₂/У_F2. В формулу для определения напряжения изгиба подставляем величины У_F и _F того зубчатого колеса пары, для которого меньше _F /У_F;

_Ft – удельная расчетная окружная сила при расчете на выносливость по

напряжениям изгиба

.

Может оказаться, что _F значительно меньше _F и это не является противоречивым или недопустимым, так как нагрузочная способность большинства передач ограничивается контактной прочностью, а не прочностью на изгиб.

Если же расчетные напряжения превышают допускаемые в пределах 5%, в перерасчете нет необходимости. При большем превышении можно принять более прочный материал, или увеличить модуль.

3.20. Выполняем проверочный расчет зубьев по предельным напряжениям при перегрузках. (см. раздел 7).