5. Включение дополнительных ограничений.

Экономическая ситуация, в которой приходится решать производственные и плановые задачи, изменяется. Может оказаться так, что некоторый ресурс, считавшийся ранее неограниченным, окажется лимитирован. Например, введение веерного распределения электроэнергии т.п. Другими словами, необходимо проверить. Удовлетворяет ли рассчитанный план новым ограничениям, и как его изменить, если ограничения нарушаются.

Итак, пусть - новое дополнительное ограничение к уже решенной задаче. То есть х* уже найдено.

Если найденное х* = (х₁, х₂, … , х_n) удовлетворяет поставленному дополнительному ограничению, то план никак не изменится (ограничение не ограничивает данное производство).

Если х* = (х₁, х₂, … , х_n) не удовлетворяет новому ограничению, то необходимо изменить план, то есть продолжить решение.

Чтобы продолжить решение. Необходимо учесть новое ограничение, записав его в каноническом виде, соответствующем оптимальной таблице: дополнительное ограничение должно содержать одну переменную с коэффициентом 1, и чтобы в других уравнениях и выражении целевой функции она отсутствовала, кроме того, это уравнение не должно содержать базисных переменных оптимальной таблицы. Чтобы исключить базисные переменные оптимальной таблицы, используют оптимальный канонический вид. При этом решение продолжается двойственным симплекс-методом.

Пример.

6. Двойственный симплекс-метод.

Для решения задачи двойственным симплекс-методом она должна иметь недопустимый канонический вид. И признак оптимальности должен выполняться.

Общая идея: начиная с недопустимого базисного решения при выполнении признака оптимальности, последовательно перейти к допустимому базисному решению, сохранив признак оптимальности.

Правила.

1. Недопустимый канонический вид ограничений и оптимальный вид (С_j )

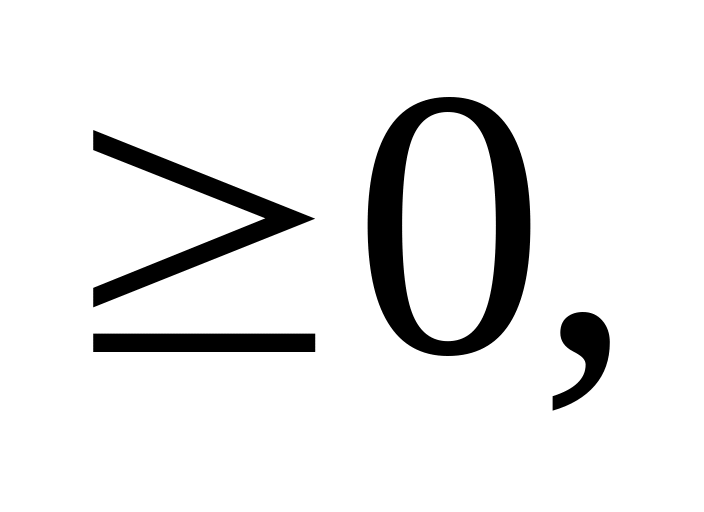целевой функции записывают в исходную таблицу.

2. Среди отрицательных свободных членов выбирают 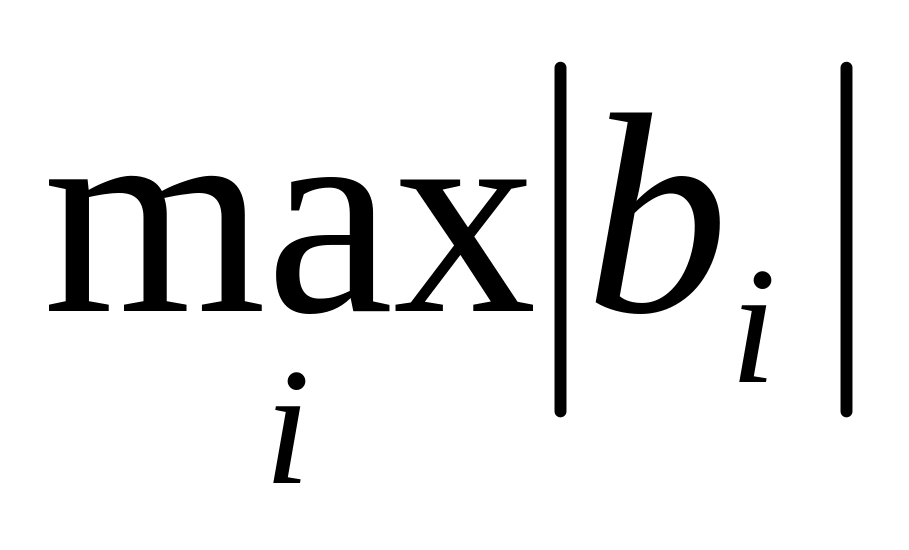, соответствующую строку помечают * и называют разрешающей.

3. Среди всех отношений коэффициентов целевой функции к отрицательным элементам разрешающей строки выбирают 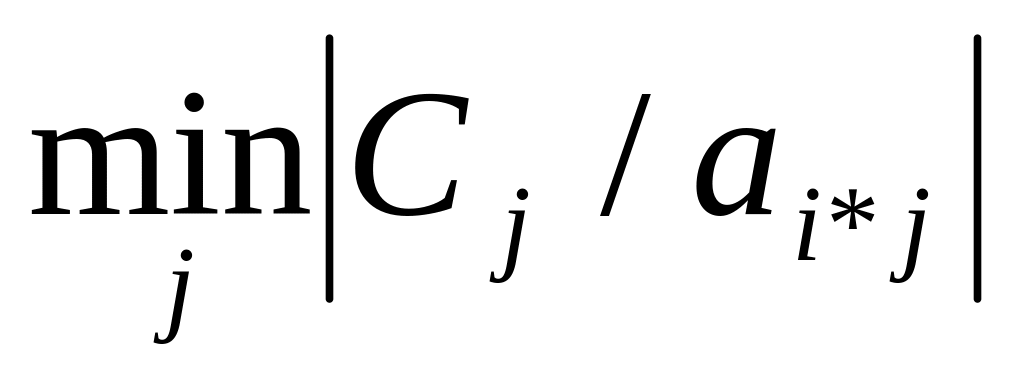, соответствующий столбец помечают * и называют разрешающим.

4. выполняют обычные симплекс-преобразования.

Замечание: 1. Обычный симплекс-метод при сохранении допустимости решения

переходит последовательно к оптимальному решению. А двойственный

симплекс-метод при сохранении оптимальности переходит

последовательно от недопустимого решения к допустимому.

2. Правила двойственного симплекс-метода отличаются от правил обычного

выбором разрешающих столбца и строки.

3. Если в разрешающей строке (для двойственного метода) нет ни одного

отрицательного элемента, то задача не разрешима.

7. Проблемы вырождения, зацикливания.

Как правило, все базисные переменные отличны от нуля (то есть в симплекс-таблице все свободные члены ). Однако, нет никаких ограничений к тому, чтобы одна или несколько базисных переменных обратились в ноль.

Базисное решение (базис) является невырожденным, если оно содержит ровно m отличных от нуля компонент. В противном случае – вырожденным.

Если начальный план задачи невырожден, то никаких сложностей при решении не возникает, при правильном выборе разрешающего элемента. Если хотя бы одна базисная переменная в НДБР приняла нулевое значение, то по правилам симплекс-метода именно она должна будет войти в базис на следующем шаге, так как min b_i/a_ij* = 0. При этом значение целевой функции не изменится.