ГОСы / Avdeenko_Otvety_1

Оглавление

2

1 Многокритериальное ПР. Качественный и количественный анализ. Пространственные модели.

Принятие решения — это процесс рационального или иррационального выбора альтернатив, имеющий целью достижение осознаваемого результата. Различают нормативную теорию, которая описывает рациональный процесс принятия решения и дескриптивную теорию, описывающую практику принятия решений.

Отсюда следует различие определений однокритериальной и многокритериальной проблемы. Многокритериальной проблемой называется такая проблема, последствия принятия решения которой могут быть адекватно описаны с помощью некоторого количества критериев.

Примером такой проблемы может служить выбор площадки для строительства аэропорта. Необходимо учитывать следующие критерии:

сокращение затрат со стороны федерального пр-ва;

увеличение пропускной способности аэропорта;

сокращение времени поездки в аэропорт;

сокращение числа переселяемых людей;

уменьшение шума;

достижение политических целей;

и др.

Количественные методы (приемы) базируются на информации, которую можно получить, зная тенденции изменения параметров или имея статистически достоверные зависимости, характеризующие производственную деятельность объекта управления. Примеры этих методов анализ временных рядов, каузальное (причинно-следственное) моделирование. Качественный.

Качественные методы основаны на экспертных оценках специалистов в области принимаемых решений, например методы экспертных оценок, мнение жюри (усреднение мнений экспертов в релевантных сферах), модели ожидания потребителя (опрос клиентов).

Количественный подход

Многокритериальное ПР, пространственные модели. Произошли из области географии. Суть – минимизация расстояния от идеальной точки ЛПР до альтернативы.

3

2 ПР в условиях неопределенности. Парадигма анализа решений. Деревья решений.

Принятие решений в условиях неопределенности даже не подразумевает знание всех возможных выигрышей и степени их вероятности. Оно основано на том, что вероятности различных вариантов ситуаций развития событий субъекту, принимающему рисковое решение, неизвестны. В этом случае при выборе альтернативы принимаемого решения субъект руководствуется, с одной стороны, своим рисковым предпочтением, а с другой — соответствующим критерием выбора из всех альтернатив. То есть, решения, принимаемые в условиях неопределенности – это когда невозможно оценить вероятность потенциальных результатов. Неопределенность ситуации может быть вызвана различными факторами, например: наличием значительного числа объектов или элементов в ситуации; недостатком информации или ее неточность; низким уровнем профессионализма; ограничением по времени и др.

Таким образом оценка вероятности происходит субъективно. Мы оцениваем вероятность случайных событий, особенно в ситуации неопределенности, крайне неточно.

Субъективная оценка вероятности похожа на субъективную оценку физических величин, таких как расстояние или размер. Так, предположительное расстояние до объекта во многом зависит от четкости его изображения: чем четче виден объект, тем он кажется ближе. Именно поэтому возрастает число аварий на дорогах во время тумана: при плохой видимости расстояния часто переоцениваются, потому что контуры объектов размыты. Таким образом, использование четкости в качестве показателя расстояния ведет к распространенным предубеждениям. Такие предубеждения проявляются себя и в интуитивной оценке вероятности.

Аксиомы вероятности. Вероятность - это оценка шансов того, что данное событие произойдет.

1)

2) Сумма вероятностей исходов равна 1:

3)

Определения вероятности. Дерево решений — это графическое изображение процесса принятия решений.

1)Классическое определение (теоретическое): Число_благоприятных случаев / Общее число случаев

2)Частотное определение (используются данные наблюдений): Число_наблюдений_события / Общее число_наблюдений

3)Субъективное определение. Используется, если нет теоретической базы и данных наблюдений. При использовании этого определения необходимо обоснование и проверка аксиомы вероятностей

Парадигма анализа решения.

Парадигма — это признанная сообществом модель, устанавливающая образцы постановки проблем, принятия решений и взаимодействия между рациональным знанием и реальностью. При этом термин все чаще используется более локально. Говоря о сообществе, речь может идти о компактной социальной группе, а не обществе в целом. Во временном аспекте также наблюдается тенденция более локализованного использования термина. Можно сказать, что парадигма задает точку зрения, ракурс, микроили макроуровень восприятия и рассмотрения проблем, контекст, рамки и т.п. Особенность в том, что подобные элементы принимаются как бы по умолчанию, как естественные и не подлежащие специальному анализу. Именно этот аспект и приводит к специфическим проблемам принятия решений в условиях меняющейся парадигмы.

Простая парадигма ПР, связанная с построением дерева решений, может быть сведена к процессу из 5 ступеней:

1)Предварительный анализ - Определение проблемы и возможных альтернатив действий. ЛПР еще не решил, какой курс действий предпринять.

2)Структурный анализ - ЛПР проводит качественную структуризацию проблемы. Определяет последовательность этапов принятия решений. Определяет, как будет собирать информацию для анализа каждого этапа, какие эксперименты провести. Эти шаги расположены по порядку на дереве решений. Дерево решений имеет два типа вершин: вершины-решения и вершины-случаи.

4

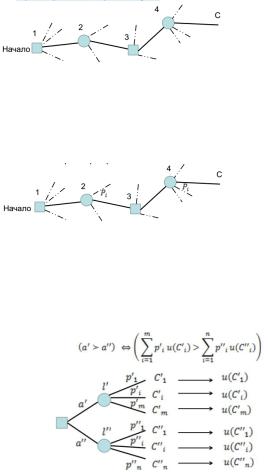
3)Анализ неопределенности - ЛПР устанавливает значения вероятностей для тех ветвей, которые начинаются в вершинах-случаях. При этом используется одно из трех определений вероятности. Полученные значения вероятностей проверяются на наличие их внутренней согласованности. Для некоторых вершин-случаев исходы могут представлять собой континуум в одно-или многомерном пространстве.

4)Анализ полезности или ценности - ЛПР устанавливает численные значения полезности последствий, связанных с реализацией всех путей на дереве решений. Один из путей Начало-1-2-3-4 имеет

последствие С. Полезность последствия С обозначим u(С).

5) Процедуры оптимизации - Максимизация ожидаемой полезности:

Деревья решений - представляют метод последовательного принятия решений и оценивания альтернатив. Дерево решений строится из следующих составляющих:

1. Выбор решения (decision fork): узел дерева, где ЛПР должен выбрать один из нескольких путей (альтернатив). Представляется квадратиком.

2. Случайный выбор (chance fork): узел дерева, где «природа» выбирает путь в соответствие с некоторой вероятностью. Представляется кружочком.

3. Плата: ветвь дерева, где необходимо заплатить некоторую сумму в случае выбора этой ветви. Представляется горизонтальной чертой, перечеркивающей путь.

5

3 Теория полезности. Принцип максимальной ожидаемой полезности. Методы прямого построения функции полезности.

Теория полезности – это теоретическое направление в экономической науке, развитое представителями австрийской школы в XIX – XX вв., основанное на базисном понятии «полезность», воспринимаемое как удовольствие, удовлетворение, получаемое человеком в результате потребления благ. Основной принцип теории полезности – закон убывающей предельной полезности, согласно которому приращение полезности, получаемое от одной добавленной единицы блага, непрерывно убывает.

Maximum Expected Utility (MEU)

Фундаментальная идея теории решений Любой ЛПР является рациональным тогда и только тогда, он выбирает действие, позволяющее достичь

наибольшей ожидаемой полезности, усредненной по всем возможным результатам этого действия. Пусть любое недетерменированное действие А имеет возможные результирующие состояния; Resulti (A) Do (A) – действие А выполняется

U (Resulti (A)) - полезность результирующего состояния Resulti(A) Тогда ожидаемая полезность определяется:

Прямое определение полезностей исходов:

1.Предположим, что в результате выбора действия А имеется n возможных случайных исходов x1,x1,…,xn. Проранжируем их по предпочтительности (от наименее предпочтительного к наиболее предпочтительному);

2.Обозначим х0 - один из наименее предпочтительных исходов, а х* - один из наиболее предпочтительных исходов;

3.Положим u(х0)=0 u(x*)=1, так как полезность не абсолютна, а относительна;

4.Рассмотрим произвольный промежуточный исход х: х0≤x≤ х* Найдем лотерею L=[ х*, π; х0, 1- π], такую что ЛПР безразличен к выбору между получением х наверняка и участием в этой лотерее;

5.Тогда (в силу безразличия0 можно приравнять полезности соответствующих исходов u(x)= π u(х*)+(1- π) u

(х0);

6.Окончательно получаем u(x)= π, т.е. полезность исхода х равна вероятности наиболее благоприятного исхода эквивалентной лотереи

Метод прямого определения полезностей может быть применен к задачам с небольшим количеством исходов Для задач с большим количеством исходов лучше использовать другой подход на основе построения

функции полезности. Этот метод предполагает:

1.Установление полезности для нескольких исходов прямым методом; 2.Подбор кривой, проходящей через найденные значения полезностей (построение функции полезности).

Полезность - это функция, которая отображает множество состояний на множество действительных чисел

U:S→R

6

4 Теория полезности. Основные свойства функции полезности. Учет отношения к риску в функции полезности.

Теория полезности – это теоретическое направление в экономической науке, развитое представителями австрийской школы в XIX – XX вв., основанное на базисном понятии «полезность», воспринимаемое как удовольствие, удовлетворение, получаемое человеком в результате потребления благ. Основной принцип теории полезности – закон убывающей предельной полезности, согласно которому приращение полезности, получаемое от одной добавленной единицы блага, непрерывно убывает.

Вид и функциональная форма функции полезности говорят очень много, например, об отношении ЛПР к риску. Поэтому первоначально необходимо установить качественные характеристики функций полезности, отражающие особенности предпочтений ЛПР. Выразив эти особенности математически, можно аналитически описать ограничения на функцию полезности, которые вытекают из наличия этих особенностей. Данный подход облегчает построение функции полезности, позволяет осуществлять автоматизацию решений.

Свойства функции полезности:

Монотонность функции полезности

1 Если исходы характеризуются в деньгах, то большинство ЛПР предпочитают большую сумму меньшей. В этом случае функция полезности удовлетворяет условию:

2 Предпочтения для периода реагирования скорой помощи. Меньший период реагирования всегда предпочтительнее большего:

3 Всегда можно перейти от убывающей функции к возрастающей: y=15-t y – сэкономленное время по сравнению с нормативным. Пример немонотонной функции полезности:

Свойство убывающей предельной полезности является следствием вогнутости функции полезности. Если функция дважды дифференцируема, то свойство означает, что вторая частная производная такой функции отрицательна

Кривая безразличия — это линия (поверхность, гиперповерхность) уровня функции полезности.

Уклонение от риска

Безразличие к риску

Стремление к риску

7

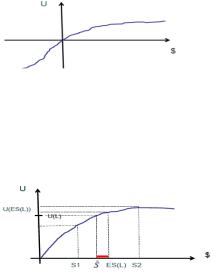
5 Теория полезности. Обоснование S- образности кривой полезности.

Теория полезности – это теоретическое направление в экономической науке, развитое представителями австрийской школы в XIX – XX вв., основанное на базисном понятии «полезность», воспринимаемое как удовольствие, удовлетворение, получаемое человеком в результате потребления благ. Основной принцип теории полезности – закон убывающей предельной полезности, согласно которому приращение полезности, получаемое от одной добавленной единицы блага, непрерывно убывает.

Предпочтения между различными уровнями задолженности могут показывать обратное поведение по отношению к вогнутости, связанной с положительными накоплениями (выпуклость). Приходим к S- образной кривой:

В положительной части кривых уклон постепенно уменьшается. В этом случае для любой лотереи L полезность решения, в котором ЛПР сталкивается с выбором в этой лотерее, меньше, чем полезность получения ожидаемого денежного выигрыша в этой лотерее

U(L)<U(ES(L))

8

6 Теория полезности. Определение отношения к риску на основе понятия детерминированного эквивалента.

Теория полезности – это теоретическое направление в экономической науке, развитое представителями австрийской школы в XIX – XX вв., основанное на базисном понятии «полезность», воспринимаемое как удовольствие, удовлетворение, получаемое человеком в результате потребления благ. Основной принцип теории полезности – закон убывающей предельной полезности, согласно которому приращение полезности, получаемое от одной добавленной единицы блага, непрерывно убывает.

Сумма, которую ЛПР готов приобрести вместо лотереи (ЛПР безразличен между выбором лотереи и этой суммой), называется детерминированным эквивалентом (эквивалентом определенности) лотереи.

9

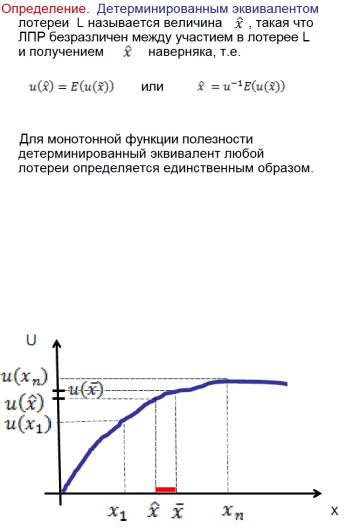
7 Определение детерминированного эквивалента. Детерминированный эквивалент для выпуклой и вогнутой функции.

Детерминированный эквивалент случайной величины X. В теории полезности - количество, имеющее ту же полезность, что и X. При заданной функции полезности U вычисляется по формуле

d(X) = U-1(EU(X)),

где U-1 - функция, обратная к U. Детерминированный эквивалент может выступать в качестве цены риска в операциях обмена.

Детерминированный эквивалент для вогнутой функции полезности:

Говорят, что ЛПР с вогнутыми кривыми полезности избегают риска. В отрицательной области с выпуклыми кривыми полезности ЛПР характеризуется стремлением к риску. Сумма, которую ЛПР готов приобрести вместо лотереи (ЛПР безразличен между выбором лотереи и этой суммой), называется детерминированным эквивалентом(эквивалентом определенности) лотереи. Разность между ожидаемым денежным значением лотереи и ее детерминированным эквивалентом называется страховой премией.

10