ГОСы / Avdeenko_Otvety_1

8 Стратегическая эквивалентность функций полезности. Линейная функция полезности.

Линейная функция полезности

11

9 Логарифмическая функция полезности. Пример.

Логарифмическая функция полезности (функция Бернулли):

где .

ПРИМЕР: Пусть u(x)=log(x+b), x>-b. Предположим, что ЛПР имеет дело с лотереей L={x1, 1/2; x2, 1/2}. Найти ожидаемый выигрыш и детерминированный эквивалент.

log(̂ )=0.5u(x1)+0.5u(x2)

log(̂ )=0.5log(x1+b)+0.5log(x2+b)

̂=√

̂=√

Для каждой лотереи детерминированный эквивалент всегда меньше, чем ожидаемый выигрыш

12

10 Экспоненциальная функция полезности. Пример.

Экспоненциальная функция полезности:

где .

13

11 Квадратичная функция полезности. Пример.

Квадратичная функция полезности:

где , -транспонированный вектор х, В - отрицательно определенная -матрица.

Пример

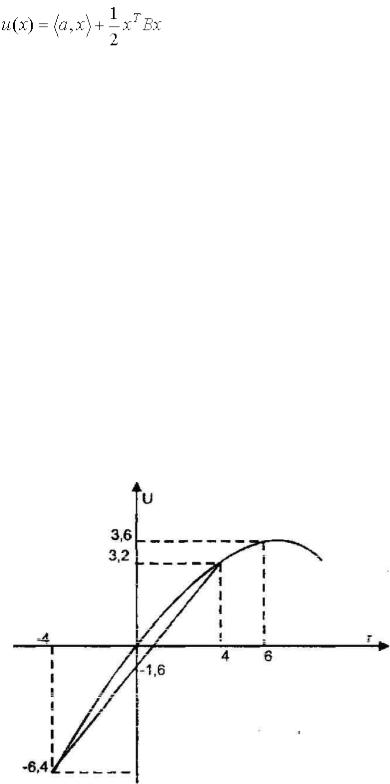
Рассмотрим простейшую иллюстрацию выбора по максимуму D ожидаемой полезности u (r) = ar + Ьr2 (а > О, Ь < 0).

Возьмем два различных инвестиционных портфеля. При одинаковой ожидаемой величине отдачи один из них не связан с риском (доход полностью определен), а другой связан с риском.

Характеристики рискового портфеля зададим следующей таблицей распределения: R - случайный доход - 4 4 Р - вероятности 0,5; 0,5

Этот портфель сулит приращение вложенных средств на 4 ед. с вероятностью 0,5 или их потерю на те же 4 ед. с той же вероятностью 0,5.

Второй портфель с риском не связан и не обещает никаких изменений с вложенными средствами, зато позволяет сохранить их без всяких потерь. Иначе говоря, индивид сберегает, но не инвестирует, то есть данный портфель содержит только деньги.

Пусть функция полезности

U(r) = 1,2г - 0,1 г2.

Так как для первого портфеля доход R - случайная величина, то и U(R) - случайная величина U(R) U(- 4) = -

6,4 U(4) = 3,2 Р 0,5 0,5

Посчитаем для него ожидаемую величину полезности:

Ec = Е(u(R)) = 0,5(- 6,4) + 0,5 х 3,2 = - 1,6.

Для второго портфеля доход есть неслучайная величина г = 0 и его полезность и(г = 0) = 0 также неслучайна, а потому ее ожидаемое значение совпадает с ней самой и равно нулю.

Таким образом, для безрискового портфеля величины ожидаемой по-лезности больше (0 > - 1,6), то есть инвестор предпочтет деньги.

Графически это решение выглядит следующим образом (

Рис. 22. График простейшего выбора

14

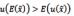
12 Теоремы о несклонности к риску. Надбавка за риск.

*Определение. ЛПР не склонен к риску, если он предпочитает получить наверняка ожидаемый выигрыш в любой невырожденной лотерее вместо участия в этой лотерее.

*В этой ситуации полезность ожидаемого выигрыша любой лотереи должна быть больше ожидаемой полезности этой лотереи. Таким образом, ЛПР не склонен к риску, если для любой невырожденной лотереи

*Теорема 2. ЛПР не склонен к риску тогда и только тогда, когда его функция полезности вогнута. *Следствие. ЛПР, который предпочитает получение наверняка ожидаемого выигрыша любой лотереи [x1,0.5; x2,0.5] (для любых неравных друг другу x1 и x2) участию в самой лотерее, не склонен к риску.

*Теорема 4. При возрастающих функциях полезности ЛПР не склонен к риску тогда и только тогда, когда его детерминированный эквивалент для любой невырожденной лотереи меньше, чем ожидаемый выигрыш в этой лотерее.

*Определение. Надбавкой за риск к лотерее называется разность между ее ожидаемым выигрышем и детерминированным эквивалентом:

*Теорема 5. При возрастающих функциях полезности ЛПР не склонен к риску тогда и только тогда, когда надбавка за риск для него положительна для всех невырожденных лотерей.

По своему физическому смыслу надбавка за риск – это сумма (в единицах измерения критерия X), которую принимающий решение согласен «уступить» из среднего выигрыша за то, чтобы избежать риска, связанного с данной лотереей.

15

13 Теоремы о склонности к риску. Надбавка за риск.

*Определение. ЛПР склонен к риску, если он предпочитает участие в любой невырожденной лотерее получению наверняка ожидаемого выигрыша этой лотереи.

В этой ситуации полезность ожидаемого выигрыша должна быть меньше, чем ожидаемая полезность лотереи, т. е. [ ̃ ] [ ̃ ].

*Теорема 3. ЛПР склонен к риску тогда и только тогда, когда его функция полезности выпукла.

*Теорема 6. При возрастающих функциях полезности ЛПР склонен к риску тогда и только тогда, когда его детерминированный эквивалент для любой невырожденной лотереи больше, чем ожидаемый выигрыш в этой лотерее.

Надбавка за риск для возрастающих функций полезности определена как разность между ожидаемым выигрышем и детерминированным эквивалентом. Исходя непосредственно из этого определения, мы получаем теорему 7.

*Теорема 7. При возрастающих функциях полезности ЛПР склонен к риску тогда и только тогда, когда надбавка за риск для него отрицательна для всех невырожденных лотерей.

16

14 Пример функции полезности для ЛПР, несклонного к риску.

У лиц, не склонных к риску, психологические переживания в связи с потерей некоторой суммы денег являются более сильными, чем удовлетворение от выигрыша такой же суммы.

Это означает, что для такого ЛПР, обладающего богатством в размере х0 рублей, функция полезности должна удовлетворять условию:

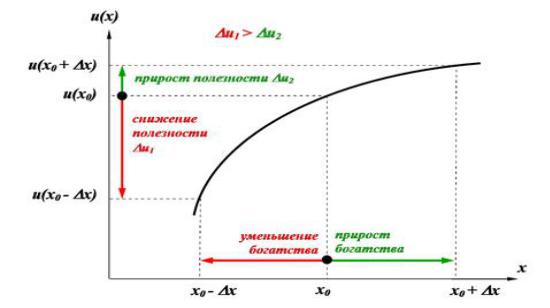
u(x0) - u(x0 - х) > u(x0 + х)- u(x0), где:

u(x0) - u(x0 - х) - отражает уменьшение полезности (то есть меру переживаний, неудовлетворения) из-за потери х рублей,

u(x0 + х) - u(x0) - отражает увеличение полезности (то есть меру удовлетворения) от выигрыша такой же суммы х.

Данное условие выполняется, если функция полезности является "выпуклой вверх".

На нижеприведённом рисунке хорошо видно, что выпуклая вверх функция u(x)действительно отражает большую "чувствительность" ЛПР к возможным потерям, чем к выигрышам.

На графике изображена функция полезности ЛПР несклонного к риску. В данной ситуации при достижении детерминированного эквивалента (доход = 150 000) происходит перегиб функции, и рост полезности от увеличивающейся суммы дохода сильно замедляется.

17

15 Пример функции полезности для ЛПР, склонного к риску.

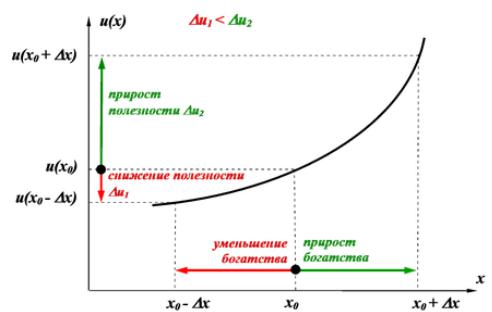
Для ЛПР, любящего рисковать, психологические выгоды от возможности выиграть х рублей превосходят переживания из-за такой же потери. Подобное отношение к риску описывается "выпуклой вниз" функцией полезности (рисунок ниже):

Из графика видно, что предельная полезность богатства инвестора склонного к риску возрастает по мере роста его богатства. Кроме того, при изменении богатства на одинаковую величину при его росте его предельная полезность увеличивается в большей степени в сравнении с ее падением при уменьшении богатства. В результате, среди активов с одинаковым ожидаемым доходом, но разным риском, инвестор предпочтет более рискованный актив. Поскольку функция полезности не склонного к риску инвестора является возрастающей, то ее первая производная положительна, т.е. U'(w) > 0. Предельная полезность является величиной возрастающей, поэтому вторая производная функции полезности также положительна,

т.е. U"(w) > 0.

18

16 Мера несклонности к риску. Обоснование. Интерпретация функции несклонности к риску.

*Для установления меры «несклонности к риску» необходимо учесть, чтобы такая мера:

1)Указывала, что отражает функция полезности – несклонность или же, напротив, склонность к риску (т.е. включала u’’) ;

2)Была бы одинаковой для стратегически эквивалентных функций.

Если u1 и u2 стратегически эквивалентные функции, то u2 = a + b u1,

→ u2’ = b u1’ u2’’ = b u1’’ u2’’/u2’ = u1’’/u1’

Таким образом, подходящей мерой является u’’/u’

*Определение. Локальная несклонность к риску в точке x определяется с помощью функции несклонности r(x)= - u’’(x)/ u’(x)

С вычислительной точки зрения полезно заметить, что r(x)= - (d/dx) [log u’(x)] ≡ - тождественно равно (не зависимо от значений переменных)

*Теорема 8. Две функции полезности стратегически эквивалентны тогда и только тогда, когда они приводят к одной и той же функции несклонности к риску.

Док-во. Необходимость. Пусть u2 = a + b u1 u2’ = b u1’, u2’’ = b u1’’ . Тогда r2(x) ≡ - u2’’(x) / u2’(x) = - (b u1’’(x)) / (b u1’(x)) = - u1’’(x) / u1’(x) ≡ r1(x)

Интерпретация функции несклонности к риску

Обозначим - первоначальное состояние, регистрируемое по шкале критерия X. Введем дополнительно ̃

Т.е. функция несклонности к риску равна удвоенной надбавке за риск, приходящейся на единицу дисперсии лотереи ̃.

19

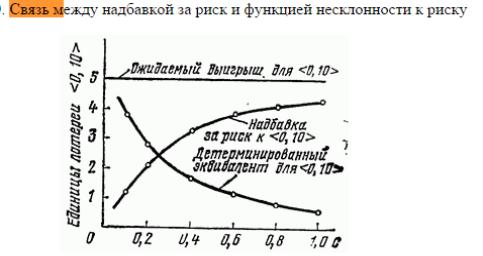
17 Связь между надбавкой за риск и функцией несклонности к риску.

На рисунке показана зависимость надбавки за риск и детерминированного эквивалента для <0,10> от параметра C функции полезности u(х)= – (при несклонности к риску).

Как и следовало ожидать, надбавка за риск к лотерее возрастет, а детерминированный эквивалент уменьшается по мере того, как возрастает несклонность к риску. Для всех значений С надбавка за риск и детерминированный эквивалент в сумме равны ожидаемому выигрышу.

20