14

Тема 7: Робота з матрицями

1. Загальні відомості

2. Робота з масивами в Excel

3. Вирішення математичних завдань в Excel

1. Загальні відомості

При вирішенні економічних завдань використовується таблиця значень, системи регресій, які зручно записувати лаконічно, з використанням матричних позначень.

Матриця - це прямокутні таблиці елементів, розташовані в рядках і стовпцях.

а₁₁ а₁₂ а_1n

[ А] = а₂₁ а₂₂ а_2n

а_m1 а_m2 а_mn

Матриця [А] називається прямокутною порядку m на n (m - число рядків, n - число стовпців). Елемент, який знаходиться в і-тому рядку і j-му стовпці, позначається через aij (і -номер рядки, j - номер стовпця).

Розрізняють: квадратна, вектор-рядок, вектор-стовпець, діагональна, одинична, нульова, симетрична.

Дві матриці А = [аij], У = [bij] називаються рівними, якщо вони мають один порядок, а відповідні елементи рівні між собою, тобто

аij = bij (i = 1, m j = 1, n)

Операції над матрицями

Складання матриць

Складання матриць здійснюється тільки для матриць одного порядку. Сумою двох матриць [А] і [В] порядку mxn називається матриця [С], яка має такий же порядок mxn, як і матриці [А] і [В], причому, кожен елемент матриці [С] дорівнює сумі відповідних елементів матриць [А] і [В], тобто

Сij = аij + bij (i = 1, m; j = 1, n)

Способи:

1. виділити комірку під елемент С₁₁ матриці С , виконати формулу з посиланням на адреси комірок з елементом а₁₁ матриці А «+» b₁₁ матриці В та розповсюдити формулу на прядок mxn.

2. Виділити матрицю А порядку mxn та скопіювати в буфер обміну. Виділити комірку з елементом b₁₁ матриці В. Команда Правка >Спеціальна вставка>Значення>додати.

3. виділити комірку під елемент С₁₁. Команда fx>Математичні>СУММ()>аргументи: адреса комірки з елементом а₁₁ матриці А; та b₁₁ матриці В. Розповсюдити функцію на прядок mxn.

Множення числа а на матрицю [A] порядку mxn називається матриця [С] порядку mхn, кожен елемент якої дорівнює добутку числа а на відповідні елемент матриці [А].

Способи:

1. Виділити комірку під елемент с11 матриці с, виконати формулу з посиланням на адресу комірки з елементом а11 та помножити на числову константу 2. Розповсюдити формулу на прядок mxn.

2. Внести значення коефіцієнту (числову константу) в комірку. Виділити комірку під елемент С₁₁ матриці С, виконати формулу з посиланням на адресу комірки з елементом а₁₁ матриці А та помножити на комірку з абсолютною адресою, яка містить множник (числову константу). Розповсюдити формулу на прядок mxn.

3. виділити комірку під елемент С₁₁. Команда fx>Математичні>ПРОИЗВЕД()> аргументи: адреса комірки з елементами а₁₁; абсолютна адреса множника. Розповсюдити функцію на прядок mxn.

4. Значення множника з комірки скопіювати в буфер обміну. Виділити діапазон матриці А порядку mxn. Команда Правка>Спеціальна вставка> Значення> помножити.

Множення матриці а на матрицю в

Можна здійснювати тоді і тільки тоді, коли число стовпців матриці А відповідає числу рядків матриці В.

За добуток матриць А і В приймається матриця C, елементи якої обчислюються за наступним правилом:

Сij = aі1 * b1j + ai2*b2j + ai3*b3j +.. .+ aim*bjn , i=1,m j=1,p

Щоб отримати елемент Сij матриці А*В необхідно i-ті рядки матриці А помножити на відповідні елементи j-х стовпців матриці В, а отриманий результат скласти.

Увага! При обчисленні елемента С₁₁ матриці С слід зафіксувати стовпці в адресах комірок для елементів, що відносяться до рядка однієї матриці, та зафіксувати рядки в адресах комірок для елементів, що відносяться до стовпця другої матриці. В такому разі при розповсюджені формули помилок не буде.

А* А² = А²*А

[А] • [Е] = [Е] • [А] = [А]

( [А] • [В] ) • [С] = [А] •( |В] • [С] )

[А| •( [В] + [С] )= [А] • [В] + [А] • [С]

Слід зазначити, що операція множення матриць не комутативна, тобто не завжди А*В = В*А.

Приклади:

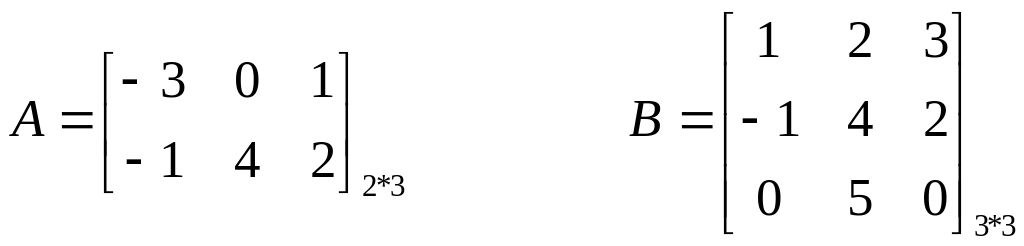
det (A • В) = det A • det В - визначник добутку матриць рівний добутку визначників цих матриць.

Мінором деякого порядку

являється визначник, який отримують шляхом умовного закреслення рядка та стовпця, на перетині яких знаходиться цей елемент:

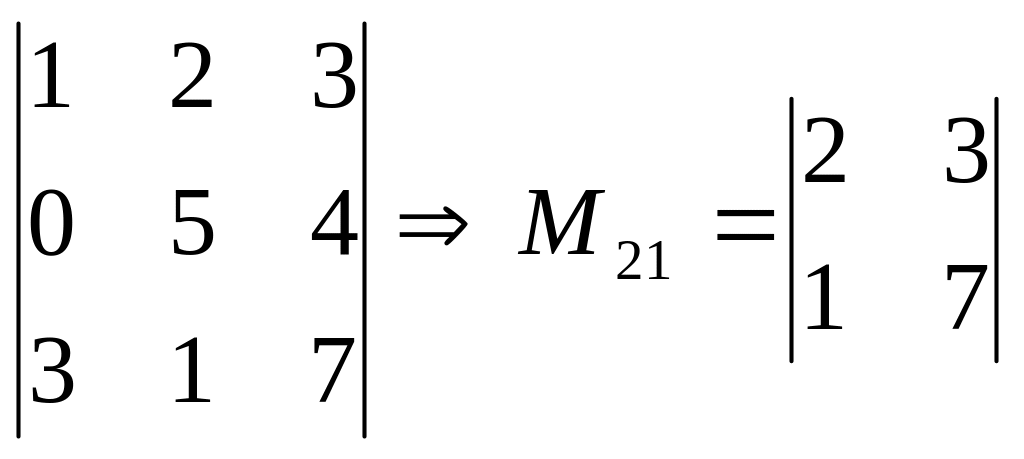
Алгебрагічним доповненням

Деякого елемента визначника називається мінор цього елемента, помножений на коефіцієнт (-1)^р, де Р – це сума номерів рядка та стовпця, на перетині яких розміщений цей елемент:

Аij=(-1)^i+j_*M_ij

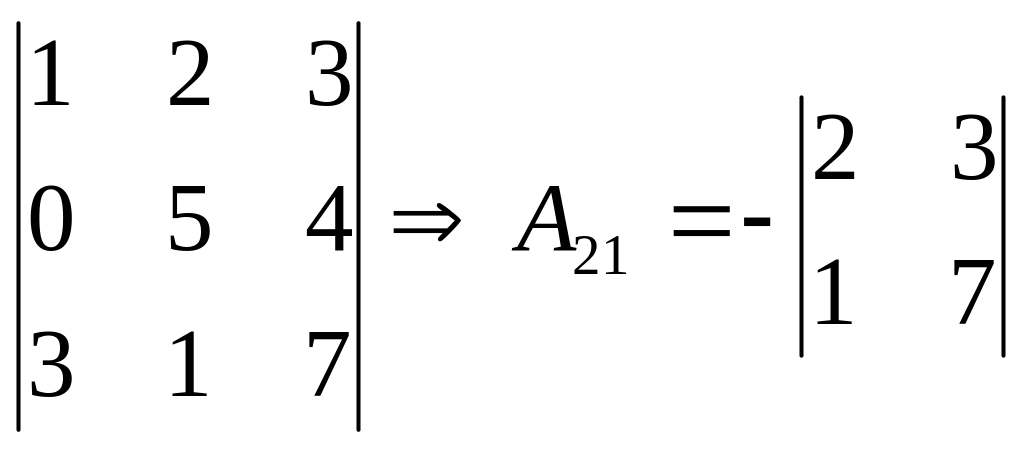
Транспонування матриць

Транспонування матриці називається заміна рядків цієї матриці її стовпцями із збереженням їх порядку.

Матриця, отримана таким чином з матриці А називається транспонованою по відношенню до А і позначається [А]^т. Для елементів транспонованих матриць виконується умова аij— аjj^T . Для симетричної матриці виконуються умови А^т =А.

Обернена матриця

Квадратна матриця [А]називається оберненою по відношенню до матриці А того ж порядку, якщо справедлива

Теорема: Для того, щоб матриця [А]^-1 мала зворотну необхідно і достатньо, щоб вона була невиродженою або невласною, тобто det А ≠ 0.

Якщо det А = 0, матриця називається виродженою або особливою.

Зворотна матриця обчислюється по правилах:

1. Обчислюється визначник матриці А.

2. Обчислюється союзна матриця, тобто матриця. складена з алгебрагічних доповнень елементів аіj матриці А:

А₁₁ А₁₂ А_1n

[ А*] = А₂₁ А₂₂ А_2n

А_m1 А_m2 А_mn

3) Транспонується союзна матриця

А₁₁ А₁₂ А_1n

[ А] = А₂₁ А₂₂ А_2n

А_m1 А_m2 А_mn

4) Обчислюється зворотна матриця:

Перевірка: А^-1*А = Е

Визначником другого порядку

відповідної матриці А, називається число

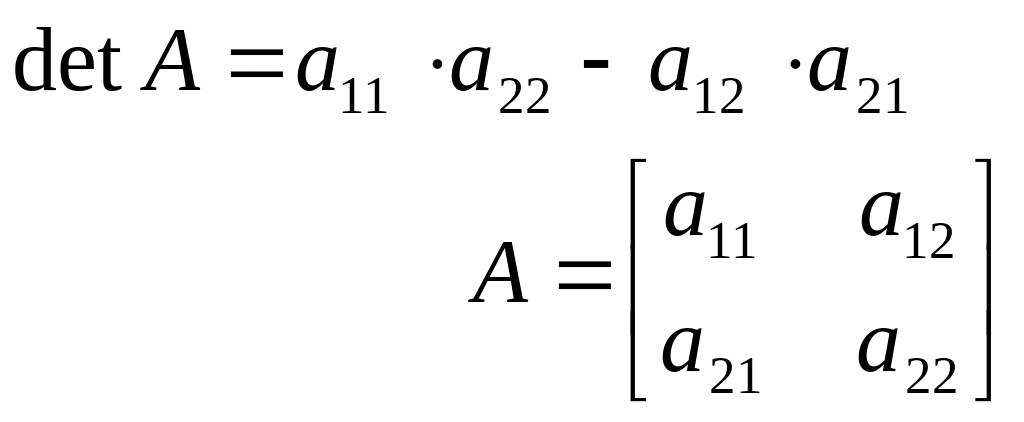
побічна і головна діагональ