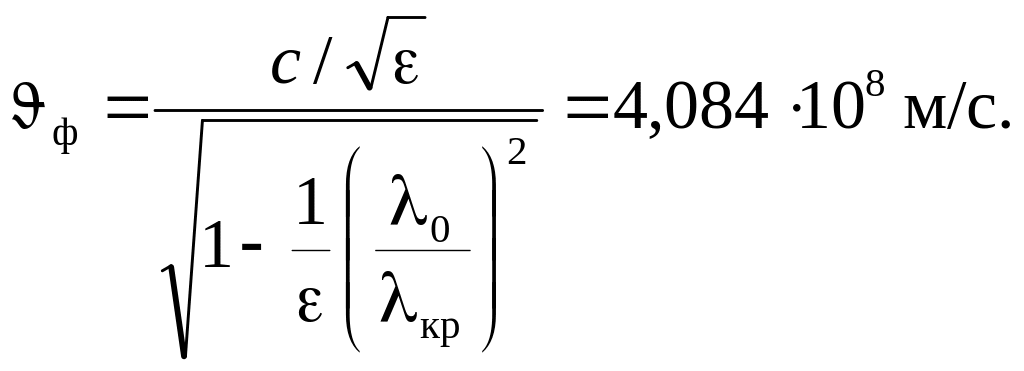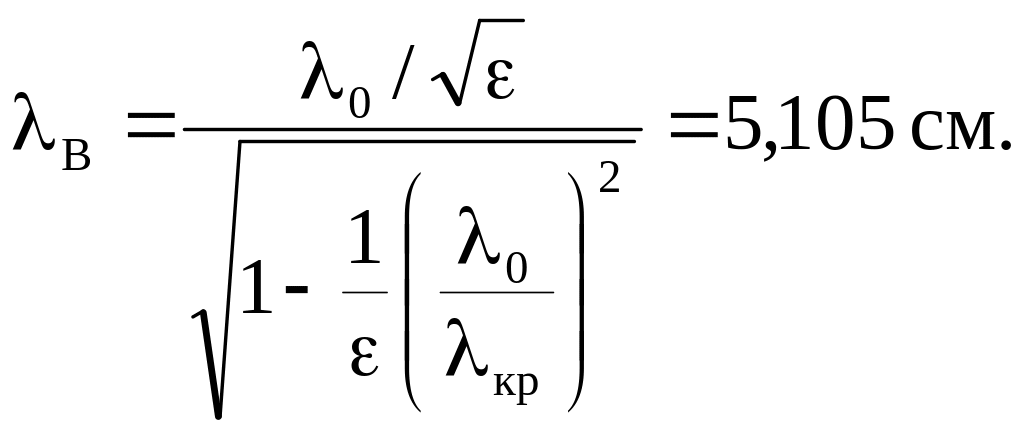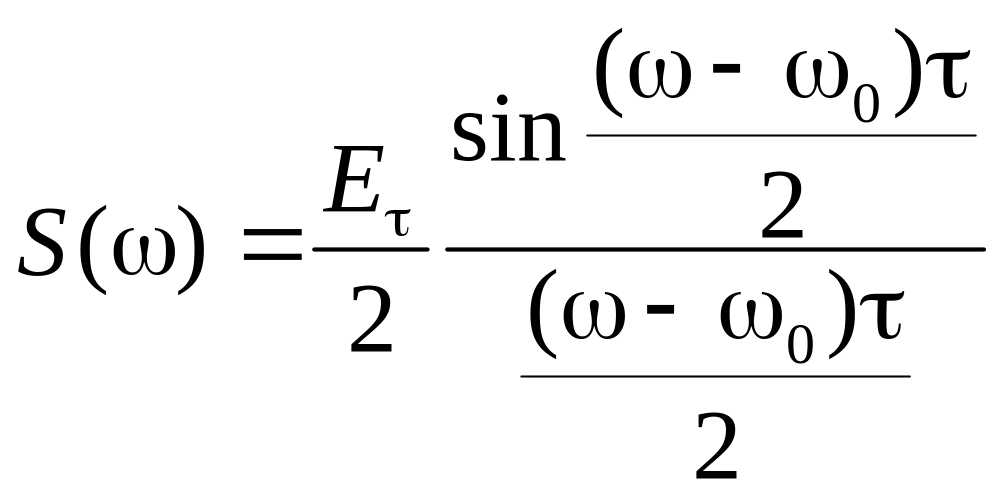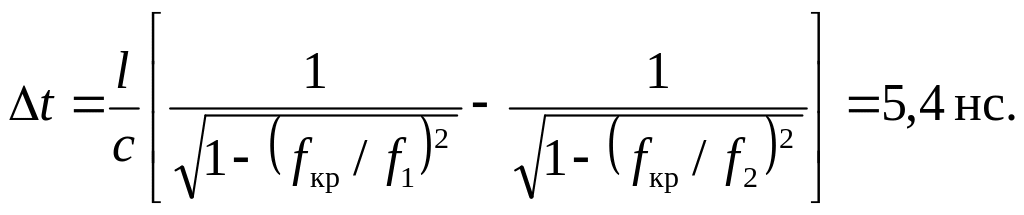§ 4.2. Приклади роз’язання типових задач

1. Які типи хвиль можуть розповсюджуватися в круглому хвилеводі діаметром 3 см, заповненому діелектриком із відносною проникністю ε = 3,2? Частота коливань 10 ГГц.

Роз’язок. У даному хвилеводі можуть розповсюджуватися лише ті типи хвиль, для яких виконується умова λ_д < λ_κρ, де λ_д = λ_0/   = c / (f  ) — довжина хвилі в однорідному безмежному діелектрику. У нашому випадку λ_д = 1,675 см. Критична довжина хвилі в круглому хвилеводі дорівнює 2a/ν_mn для хвиль типу Е_mn і 2a/μ_mn для хвиль типу Н_mn. Отже, для типів хвиль, що поширюються, повинні виконуватися умови _mn < 2πa/λ_д, μ_mn < 2πa/λ_д, 2πa/λ_д = 5,627, яким задовольняють наступні типи хвиль: Е₀₁, Е₀₂, Е₁₁, Е₂₁, h₀₁, H₁₁, H₁₂, Н₂₁, Н₃₁, Η_21.

2. У прямокутному хвилеводі перерізом 4  3 см розповсюджується хвиля типу Н₁₁. Хвилевід заповнений пенополистиролом із діелектричною проникністю ε = 1,15. Частота коливань 8 ГГц.

Визначити фазову швидкість і довжину хвилі у хвилеводі.

Роз’язок. Знайдемо критичну довжину хвилі для коливання типу Н₁₁ у прямокутному хвилеводі:

Довжина хвилі генератора λ₀ = c/f = 3,75 см.

Фазова швидкість хвилі у хвилеводі

Довжина хвилі в хвилеводі

3. При якому діаметрі круглого хвилеводу в ньому може розповсюджуватися тільки один основний тип хвилі при частоті коливань 10 ГГц?

Роз’язок. Спочатку знайдемо довжину хвилі генератора

λ0 = c/f = 3 см.

Основним типом хвилі круглого хвилеводу є хвиля Н₁₁ Її критична довжина

λκρ = 2πa/1,841 = 3,413a,

звідки отримуємо умову існування хвилі типу Н₁₁:

a > λ0/3,41 = 8,79 мм.

Найближчим вищим типом хвилі в круглому хвилеводі є хвиля Е₀₁. Її критична довжина

λкр = 2πa/2,405 = 2,613a.

Щоб хвиля типу Е₀₁ не могла розповсюджуватися, повинна виконуватися умова

a < λ0/2,61 = 11,48 мм.

Отже, діаметр хвилеводу повинен бути в межах

17,58 мм< a < 22,96 мм.

4. Прямокутний хвилевід перерізом 23  10 мм служить для передачі надвисокочастотних імпульсів із прямокутною огинаючою. Тривалість імпульсів τ = 6 нс, несуча частота f₀ = 10 ГГц. Довжина лінії l = 50 м.

Оцінити якісно величину спотворень імпульсів, викликаних дисперсією хвилеводу.

Роз’язок. Насамперед, відзначимо, що в прямокутному хвилеводі перерізом 23  10 м при частоті 10 ГГц може розповсюджуватися лише хвиля типу Н₁₀. Її критична довжина λ_κρ = 2a = 4,6 см і критична частота l_кр = з/_кр = 6,52 ГГц.

Спотворення форми імпульсів у хвилевідній лінії передачі викликані різним часом групового запізнювання для різних складових спектра сигналу. Спектр прямокутного високочастотного імпульсу в області додатних частот описується формулою

т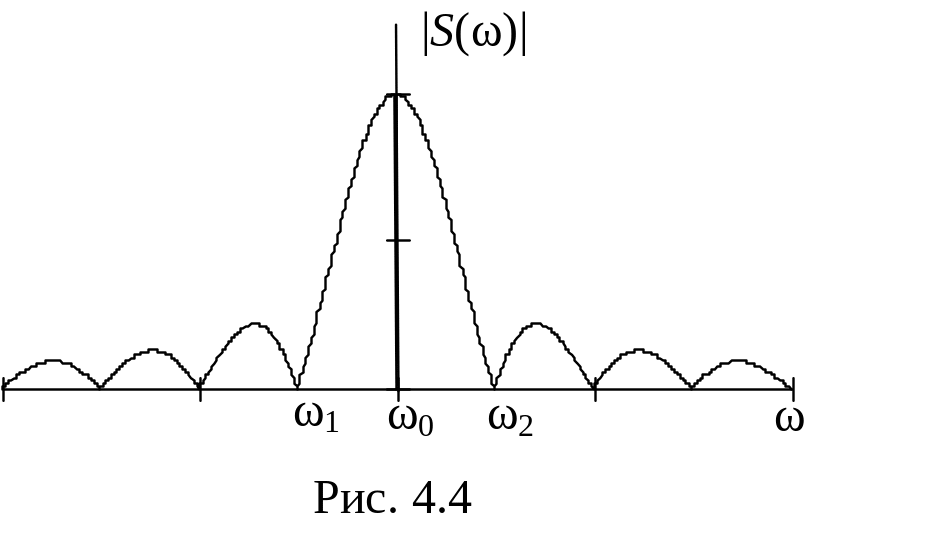 а має вигляд, зображений на рис. 4.4.

Припустимо, що ширина спектра дорівнює ширині його, головного пелюстка. Тоді крайні частоти спектра будуть рівні: f₁ = f₀ - 1/ = 9,833 ГГц, f₁ = f₀ + 1/τ = 10,167 ГГц. Різниця групового часу запізнення

(4.18)

Використовуючи рівняння ( 4 .0), одержимо