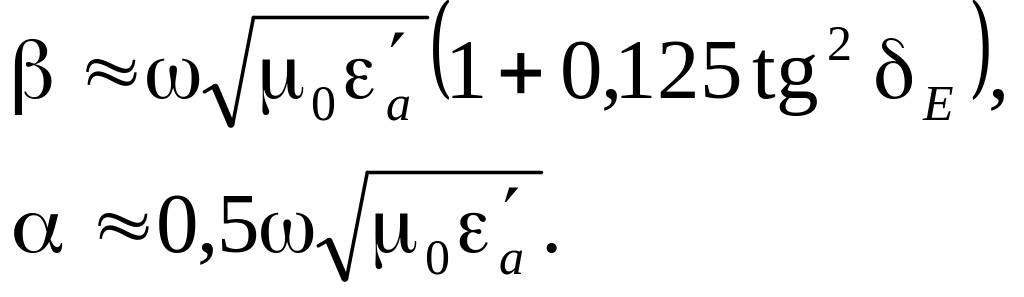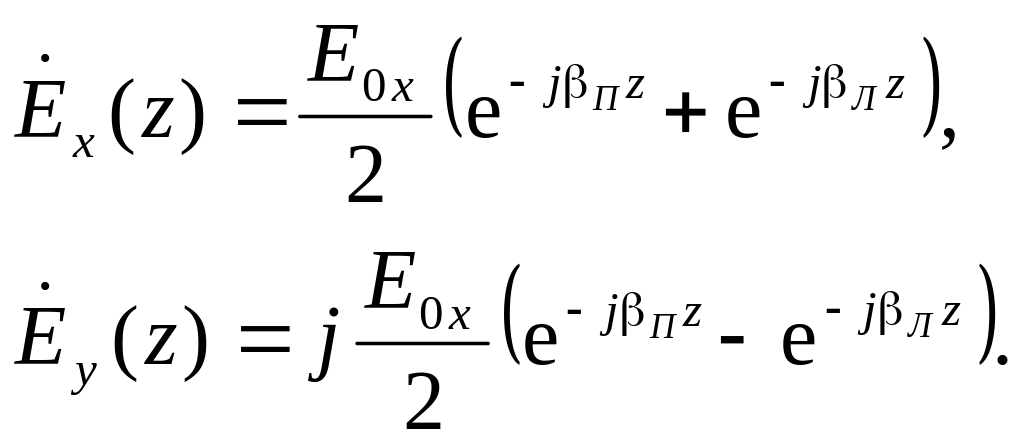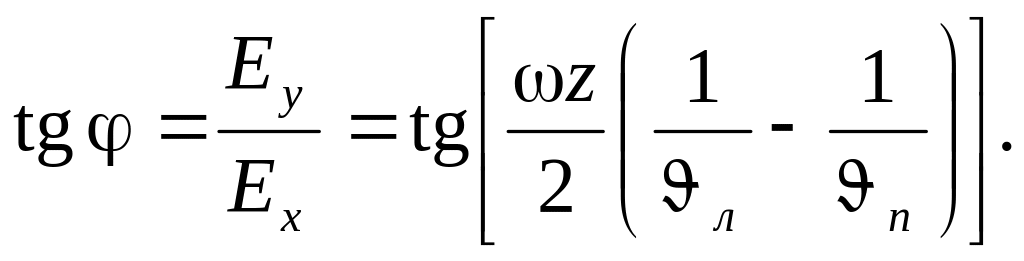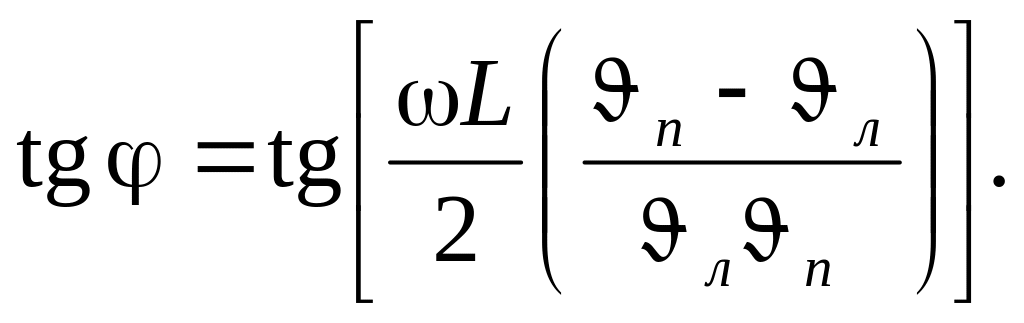§ 3.2. Приклади роз’язання типових задач

1. Плоска електромагнітна хвиля з частотою 10⁹ Гц розповсюджується в середовищі з параметрами .

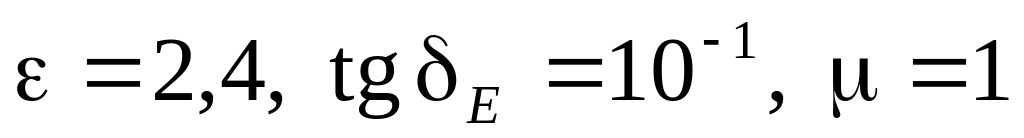Визначити фазову швидкість, довжину хвилі та коефіцієнт ослаблення.

Роз’язок. Врахуємо, що та розкладемо вираз ( 3 .0) у степеневий ряд. Обмежуючись трьома першими членами, отримаємо

Таким чином, для діелектрика з малими втратами коефіцієнт фази та коефіцієнт ослаблення наближено рівні:

Використовуючи співвідношення ( 3 .0), знайдемо фазову швидкість хвилі

Отриманий результат свідчить, що наявність втрат у середовищі призводить до зміни величини фазової швидкості. Для попттак,ка складає 0,125%, так що практично можна покласти

На основі відомої величини фазової швидкості знайдемо довжину хвилі:

Підстановка вихідних даних в отриману раніше формулу дає:

2. Обрахувати фазову швидкість, коефіцієнт ослаблення та глибину проникнення поля для плоскої електромагнітної хвилі з частотою 10 МГц, що розповсюджується в металі з параметрами

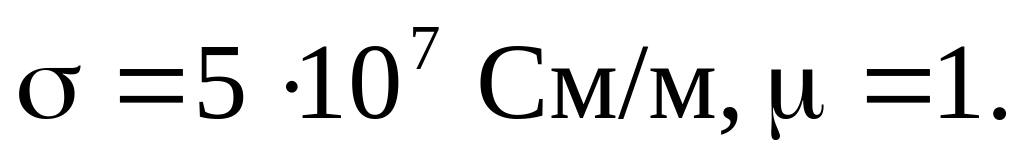
Роз’язок. У реальних металах густина струмів провідності значно більша густини струмів заміщення. Тому вираз ( 3 .0) можна наближено записати у вигляді

Коефіцієнт фази та коефіцієнт ослаблення у середовищі, що розглядається, чисельно рівні одне одному:

На основі відомої величини  можна обчислити фазову швидкість:

За глибину проникнення поля в метал d приймають відстань, на якій його амплітуда зменшується в е раз. Очевидно, що

3. Плоска електромагнітна хвиля з частотою 10⁹ Гц розповсюджується в середовищі з параметрами 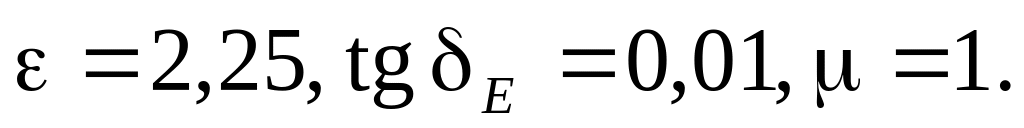Амплітуда електричного поля в площині z = 0 дорівнює 100 В/м.

Визначити середню густину потоку потужності в площині z = 1 м.

Роз’язок. Густина потоку потужності плоскої електромагнітної хвилі визначається виразом

Таким чином, необхідно обчислити коефіцієнт ослаблення та характеристичний опір. Діючи так само, як і в задачі 3.1, можна знайти . Підстановка вихідних даних дає .

При визначенні характеристичного опору для , можна використати наближений вираз для квадратного кореня, що входить до формули ( 3 .0). Тоді

Звідки,

Або після необхідних обчислень

4. Деякі речовини (наприклад, водний розчин цукру) мають різну швидкість розповсюдження для хвиль із лівою та правою круговою поляризаціями. Це призводить до повороту площини поляризації плоскої хвилі з лінійною поляризацією в процесі її розповсюдження. Така властивість речовин зветься оптичною активністю.

Вважаючи, що значення фазових швидкостей для лівої та правої кругової поляризації задані, вивести формулу, яка визначає кут повороту площини поляризації хвилі на проміжку ізляху довжиною L для електромагнітної хвилі з заданою частотою .

Розв’язок. Лінійно поляризовану хвилю, що в площині z = 0 має вигляд

Можна представити як суму двох хвиль із круговою поляризацією:

Хвиля із правою круговою поляризацією при розповсюдженні в напрямку осі z буде описуватися виразом

а з лівою – виразом

У довільній площині сума цих хвиль являтиме собою хвиля з лінійною поляризацією. Координатні компоненти цієї хвилі рівні:

Сумарний вектор Е утворює деякий кут  з віссю х координатної системи (х, у, z), який залежить від z. Тангенс цього кута

Таким чином, кут повороту площини поляризації на відрізку шляху довжиною L визначається формулою

Зазвичай відмінність швидкостей розповсюдження та мала. Тому наближено

де  – середнє значення швидкості;  – відносна різниця швидкостей розповсюдження;  – довжина хвилі в середовищі.