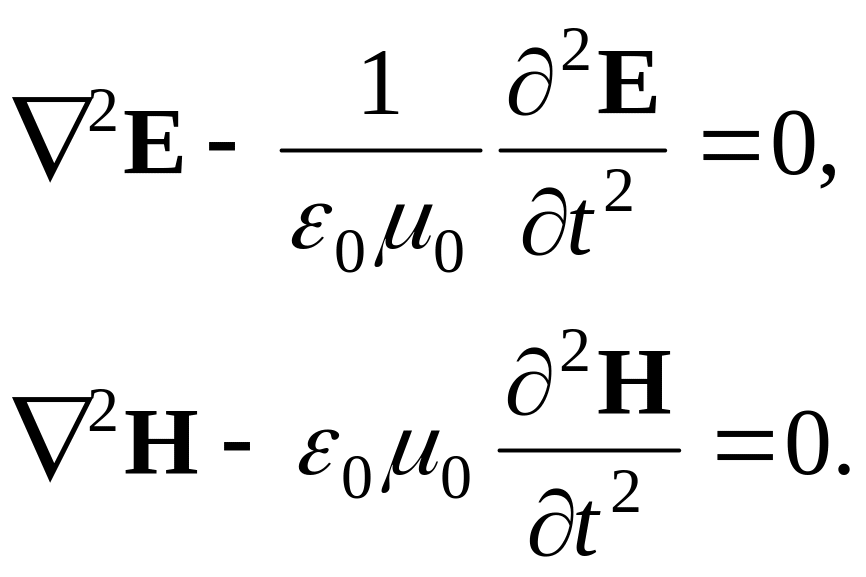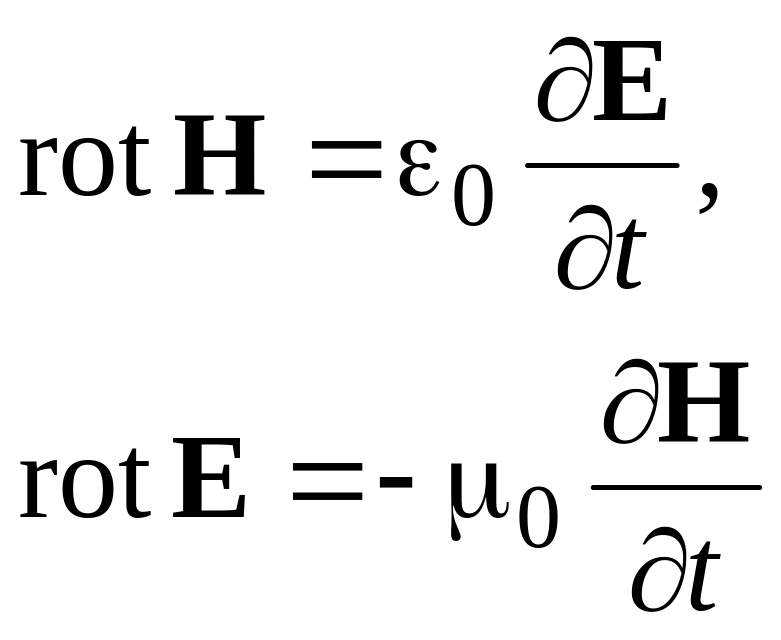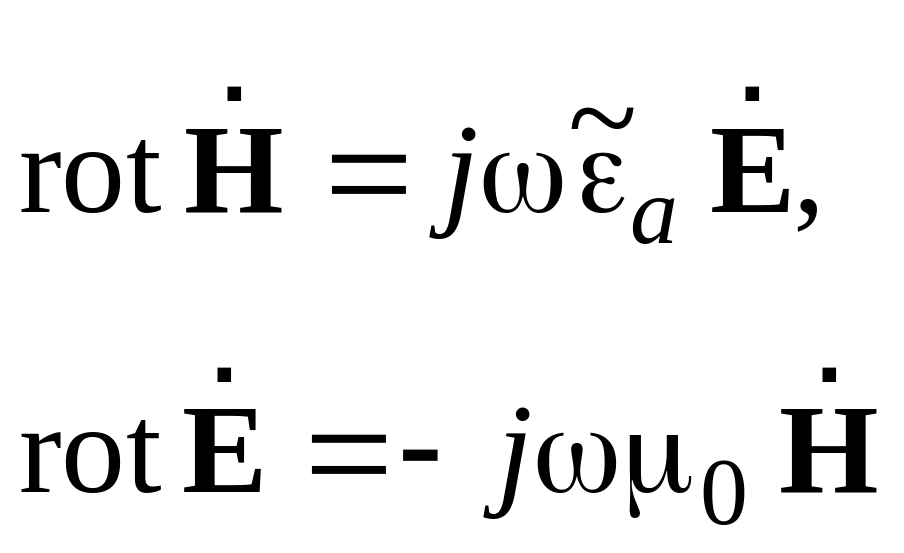§ 2.2. Приклади роз’язання типових задач

1. У вакуумі існує електромагнітне поле, що гармонічно змінюється в часі. У деякій точці простору вектор .

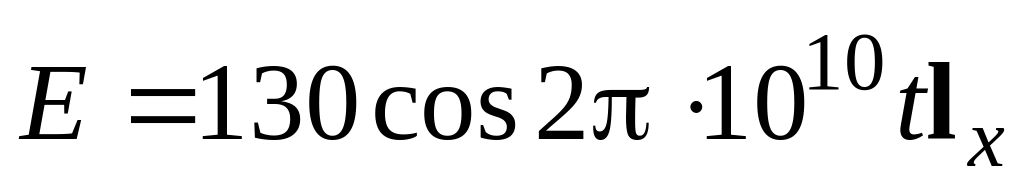Визначити густину струму зміщення в даній точці.

Роз’язок. За визначенням струм зміщення

Слід звернути увагу на те, що в просторі струм зсуву й напруженість електричного поля паралельні, однак струм випереджає по фазі напруженість поля на 90°.

2. Показати, що з рівнянь Максвела для вакууму випливають відомі хвильові рівняння

(2.25)

Роз’язок. Випишемо систему з двох перших рівнянь Максвела, справедливих для вакууму під час відсутності сторонніх джерел:

(2.26)

і застосуємо операцію rot до другого рівняння системи (2.25):

Припускаючи, що в даній області простору немає зарядів (div Е = 0) і, скориставшись першим рівнянням (2.26), одержимо хвильове рівняння (2.25) для вектора електричного поля. Рівняння щодо вектора магнітного поля знаходять аналогічно.

3. Матеріальне середовище характеризується абсолютними проникностями .

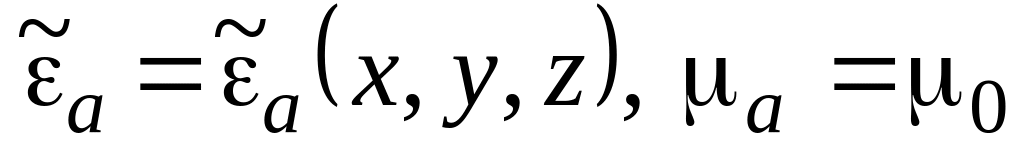Вивести диференціальне рівняння другого порядку, якому повинне задовольняти векторне поле Н у даному неоднорідному середовищі, якщо електромагнітний процес гармонічно змінюється в часі з частотою ω.

Роз’язок. Розглянемо два перших рівняння Максвела відносно комплексних амплітуд:

(2.27)

застосуємо операцію rot до першого рівняння (2.28):

Магнітна проникність середовища незмінна в просторі, тому , крім того,

Вектор Е можна виразити через вектор Н із першого рівняння

Звідси одержуємо остаточний вид шуканого рівняння

4. Показати, що рівняння неперервності струму випливає з першого і третього рівнянь Максвела ( 2 .0).

Роз’язок. Тут варто взяти до уваги відому тотожність векторного аналізу і записати

потім скористатися третім рівнянням Максвела ( 2 .0). Таким чином приходимо до рівняння неперервності

§ 2.3. Задачі для самостійного роз’язання

5. Показати, що з четвертого рівняння Максвела в неоднорідному середовищі, магнітна проникність якої є функцією просторових координат, випливає наступне рівняння для вектора напруженості магнітного поля:

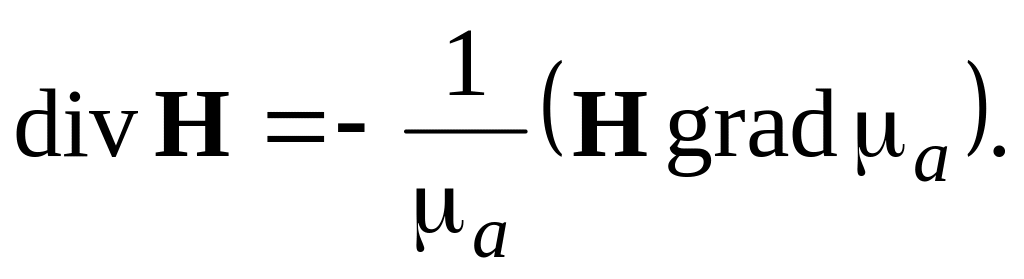
6. Показати, що електромагнітне поле, яке змінюється в часі за гармонічним законом із частотою ω в області простору, вільної від джерел, задовольняє однорідним рівнянням Гельмгольця

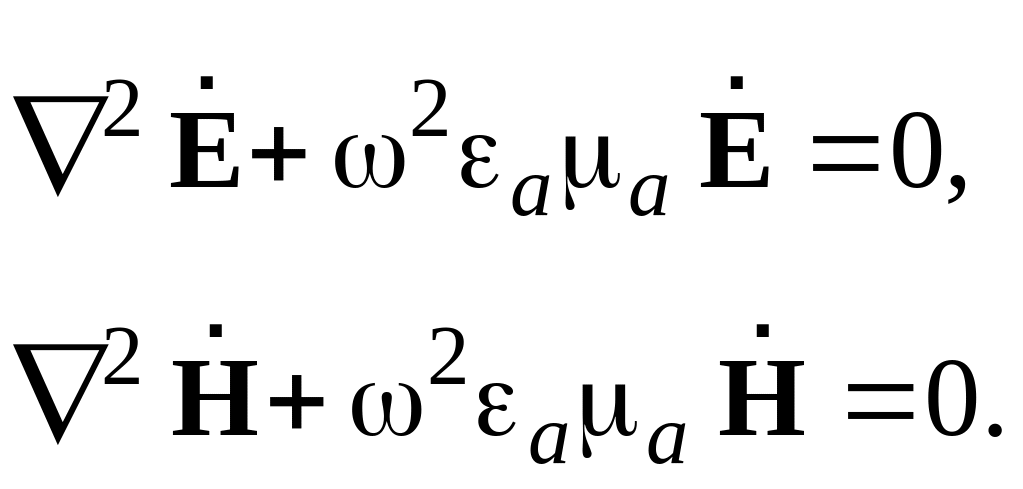
7. Вектор напруженості електричного поля Е в декартовій системі координат має єдину, відмінну від нуля, складову Е_х, .

Показати, що при цьому вектор Пойнтинга не може мати складової вздовж осі x.

8. У фіксованій точці простору відомі миттєві значення векторів поля

де E₀ і Н₀ — сталі вектори.

Показати, що миттєве значення вектора Пойнтинга складається з незмінного в часі середнього значення

і змінної частини

що змінюється в часі з подвоєною частотою.

9. При феноменологічному описі частотних властивостей полярних діелектриків використовують математичну модель, що уподібнює молекулярні диполі уявним твердим частинкам, що відчувають при своєму русі в’язкий опір навколишнього середовища. При цьому зв'язок між вектором поляризації Р та вектором напруженості електричного поля Е встановлюється диференціальним рівнянням

де а — константа; Т — час релаксації середовища.

Вивести залежність комплексної абсолютної діелектричної проникності від частоти.

Відповідь:

10. Використовуючи умови попередньої задачі, вивести формулу тангенса кута діелектричних втрат.

Відповідь:

11. Розв’язати задачу 2.9 для випадку, коли динаміка процесу поляризації описується рівнянням

де ω₀ — власна частота молекулярного диполя; b — константа. Таке рівняння виникає, якщо за модель диполя прийняти осцилятор із тертям.

Проаналізувати графіки частотних залежностей дійсної та уявної частин діелектричної проникності.

Відповідь:

12. Комплексні амплітуди векторів електромагнітного поля в деякій точці простору задаються вираженнями

Визначити комплексний вектор Пойнтинга і його середнє значення.

Відповідь: