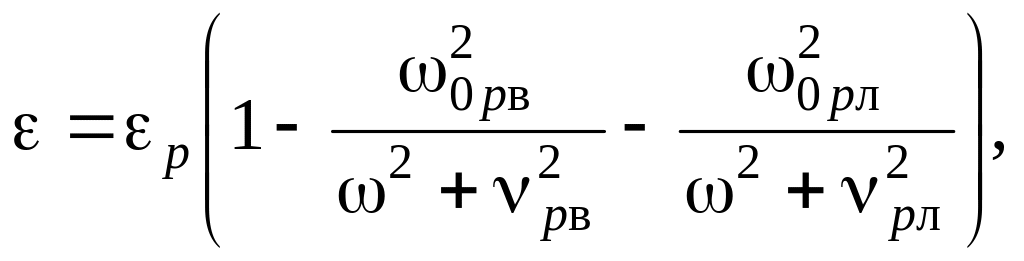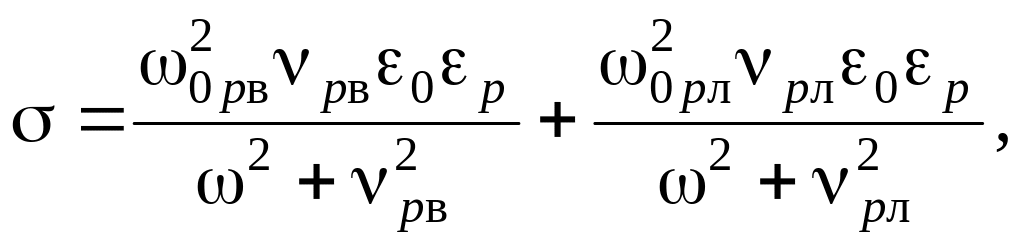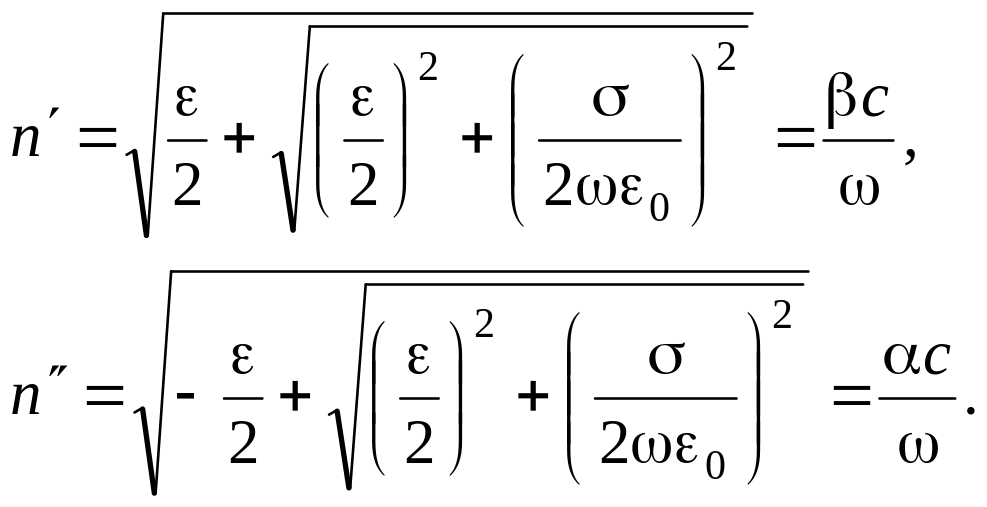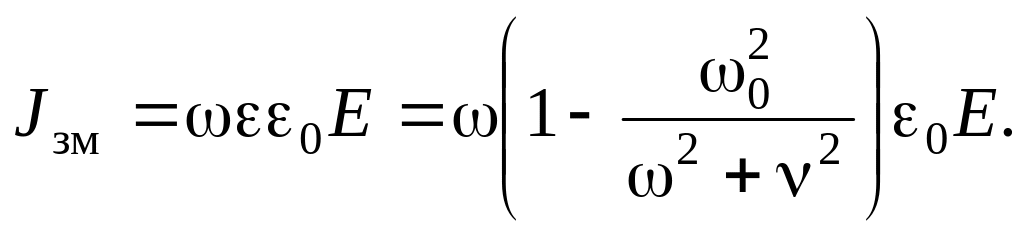§ 9.2. Приклади роз’язання типових задач

1. Використовуючи рівняння неперервності, отримати вираз для плазмової частоти електронів у плазмі без зіткнень. При виводі вважати, що струм у плазмі переноситься тільки електронами з зарядом e та масою m. Концентрація електронів дорівнює n.

Роз’язок.Нехай ρ – об’ємна густина заряду в плазмі. Густина струму провідності JЕ пов’язана зі зміною об’ємної густини заряду рівнянням неперервності

Для достатньо швидких процесів, як, наприклад, у випадку, що розглядається, можна вважати, що струм переноситься тільки найбільш легкими частинками – електронами. Тому густина струму в плазмі , де  ‑ середня швидкість електронів. Рівняння руху “середнього” електрону у плазмі без зіткнень має вигляд

З урахуванням виразу для густини струму провідності рівняння можна переписати наступним чином:

(9.15)

Продиференціювавши рівняння неперервності по t і використавши вираз (9.15) для однорідної плазми, отримаємо

Враховуючи закон Гауса, знаходимо рівняння вільних коливань об’ємної густини заряду

де  ‑плазмова частота.

2. У зразку кремнію р-типу існують дірки двох сортів. Ефективна маса важких дірок 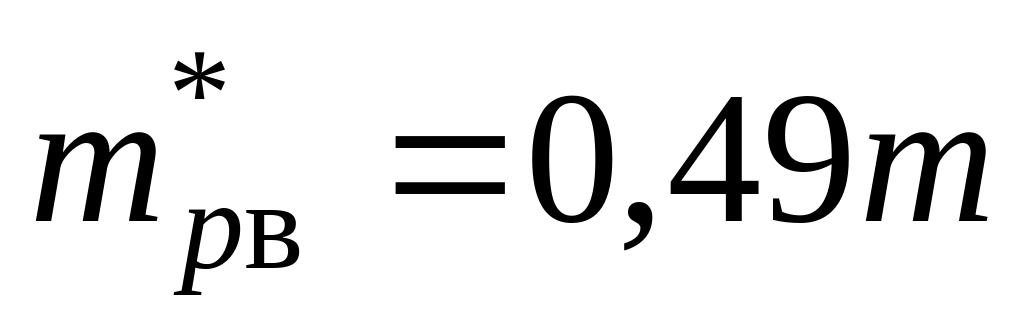(m – маса електрона), легких ‑ 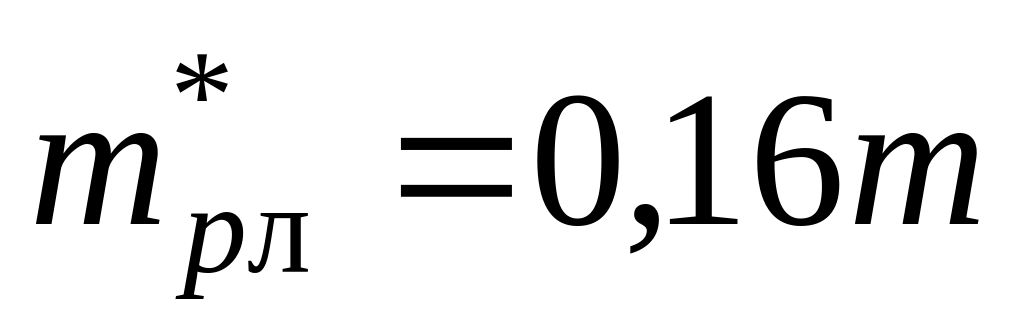. Число зіткнень за секунду важких та легких дірок у з іншими частинками складає 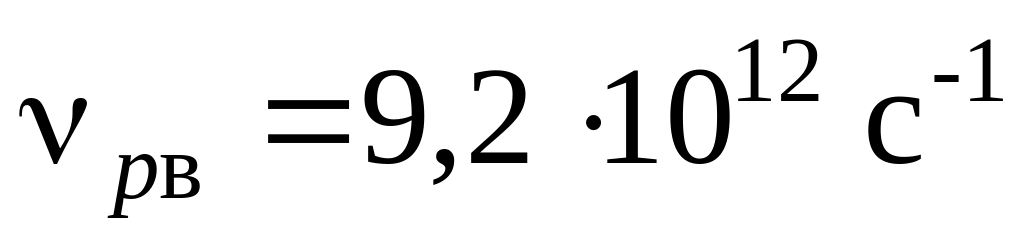та .

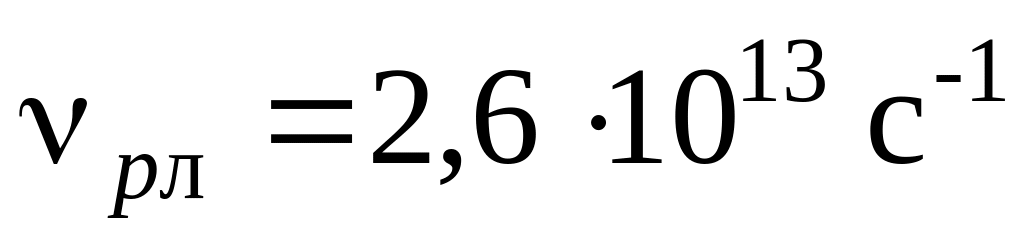Роз’язок.Оскільки даний напівпровідник містить два сорти носіїв заряду, відносна діелектрична проникність кремнію

а провідність

де ,  ‑ відповідно квадрат плазмової частоти важких та легких дірок;  ‑частота сигналу.

Підставляючи числові данні у вирази для  та , отримаємо  = 9,90;  = 194 См/м.

3. Плоска електромагнітна хвиля розповсюджується в однорідній ізотропній газовій плазмі.

Визначити відносну діелектричну проникність та провідність плазми, якщо коефіцієнти розповсюдження хвилі на частоті 0,48 ГГц рівний 5 – j 2 м^-1.

Роз’язок.Використовуючи формулу ( 9 .0), представимо дійсну та уявну частини коефіцієнта заломлення через коефіцієнт фази β та коефіцієнт ослаблення α:

Піднесемо перший та другий вираз до квадрату та віднімемо від першого отриманого співвідношення друге:

(9.16)

Обрахуємо добуток

та використаємо цей вираз для находження провідності

(9.17)

За умовою задачі β = 5, α = 2. Підставляючи ці значення до виразів (9.16) та (9.17), отримаємо  = 0,2078,  = 5,28·10^-3 См/м.

4. Знайти значення частоти сигналу хвилі, що пройшла, при якій у газовій плазмі з параметрами ω₀ = 2·10⁸ с^-1 та ν = 10⁸ с^-1 густина струму провідності дорівнює густині струму зміщення.

Роз’язок. Густина струму провідності у плазмі

Густина струму зміщення у плазмі

Прирівнюючи значення густини струму провідності та густини зміщення, отримаємо кубічне рівняння відносно частоти сигналу

У канонічній формі це рівняння має вигляд

де

Легко перевірити, що дійсний корінь останнього рівняння

де

Звідси знаходимо значення частоти сигналу, при якому J_пр = J_зм : ω = (1,55 + 0,64)·10⁸ = 2,19·10⁸ c^-1.

5. Дві плоскі лінійно поляризовані хвилі розповсюджуються у напрямі вісі х у монокристалі сапфіра (Al₂O₃), тензор діелектричної проникності якого

Визначити різницю фаз цих хвиль, що пройшли у сапфірі відстань у 1 см, якщо перша хвиля поляризована вздовж осі у, а друга – уздовж осі z. Частоти коливань однакові та дорівнюють 10 ГГц. На цій частоті _xx = _yy = 13,2, _zz = 11,4.

Роз’язок. Хвиля, що характеризується вектором , буде звичайною з коефіцієнтом фази

Хвиля, що характеризується вектором , буде незвичайною з коефіцієнтом фази

Різниця фаз при проходженні звичайною та незвичайною хвилями відстані