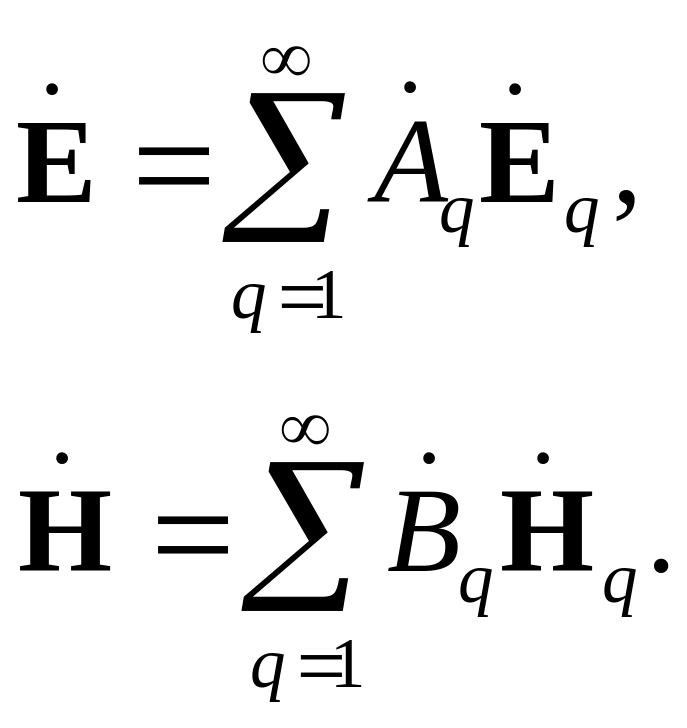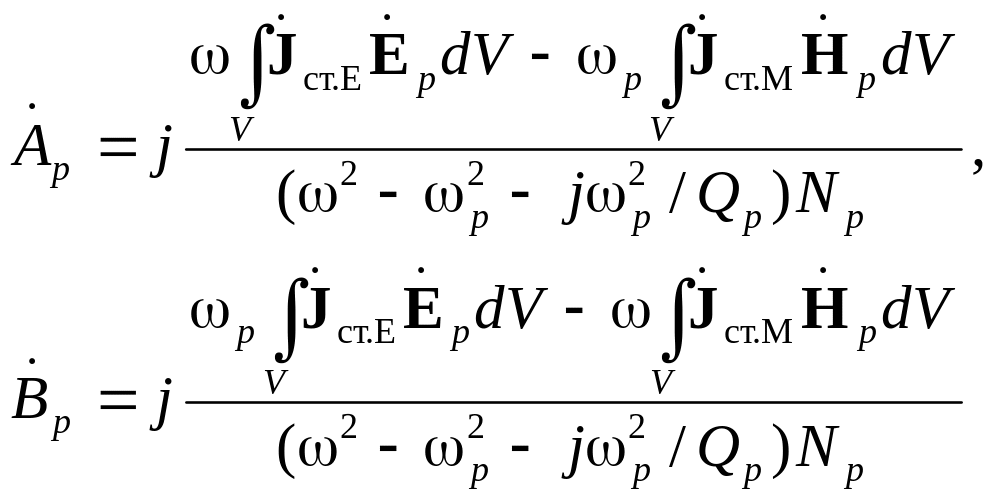Розділ восьмий збудження замкнених електродинамічних систем § 8.1. Основні теоретичні відомості

Збудження хвилеводів

Н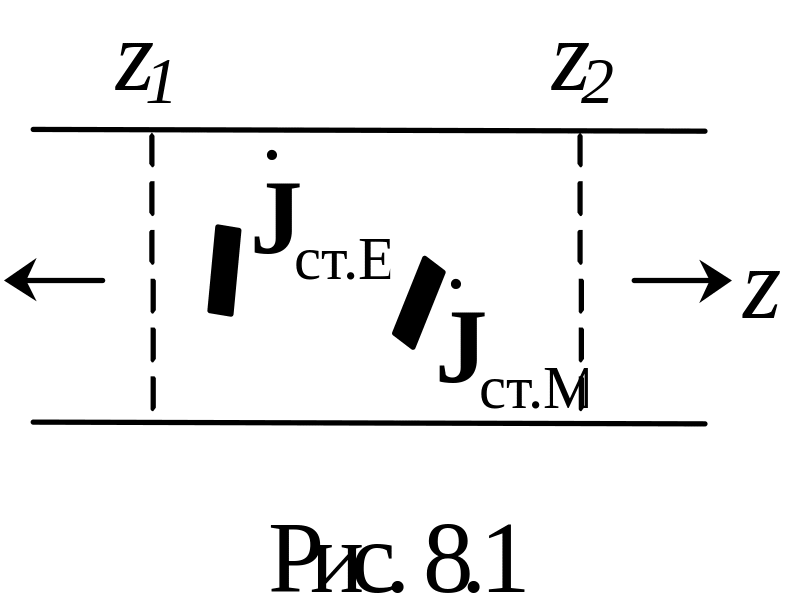 ехай у нескінченному хвилеводі джерела поля, що знаходяться в об’ємі V, обмеженому інтервалом z₁ < z < z₂ (рис. 8.1), задані функціями a, . Передбачається, що стінки хвилеводу ідеально провідні, а діелектрик, що заповнює хвилевід, не має втрат. Поле поза об’ємом V представляється у виді сукупності хвиль електричного й магнітного типів:

(8.0)

Тут n — номер типу хвилі у хвилеводі (якщо під n розуміти два індекси, то підсумовування рядів проводять за обома індексами); С_±n — коефіцієнти збудження; _±n, _±n — комплексні амплітуди векторів поля n-го типу. Знак мінус означає хвилю, що розповсюджується в від’ємному напрямі вісі z.

Ставиться задача визначення коефіцієнтів збудження. Вимушене поле ( 8 .0) задовольняє неоднорідним рівнянням Максвела. Для того щоб вирішити задачу про вимушені коливання у хвилеводі, необхідно володіти рішенням більш простої задачі про вільні поля, що задовольняють однорідним рівнянням Максвела.

Застосовуючи лему Лоренца до електромагнітного поля ( 8 .0) в об'ємі V та, використовуючи як допоміжне поле _±n, _±n, k-го типу хвиль, комплексні амплітуди якого необхідно визначити, знаходимо вирази для коефіцієнтів збудження:

(8.0)

Тут

(8.0)

— норма k-й власної хвилі.

Збуджувана джерелом k-а хвиля переносить через кожен поперечний переріз активну потужність

(8.0)

Збудження об'ємних резонаторів

Якщо об'ємний резонатор обмежений замкнутою ідеально провідною поверхнею S₀, то роз’язок рівнянь Максвела повинний задовольняти граничній умові

(8.0)

Будемо вважати, що вільні коливання резонатора відомі, тобто знайдені повна система векторних функцій , і власні частоти ω_р. Тут індекс p означає номер типу коливань в об'ємному резонаторі. Власні коливання в об'ємному резонаторі задовольняють умові ортогональності:

(8.0)

(вважається, що власні частоти всіх типів коливань різні, чи іншими словами, у резонаторі відсутнє виродження типів коливань).

Норма власного коливання

(8.0)

Електромагнітне поле, збуджене в резонаторі, відшукують у виді рядів^

(8.0)

Амплітудні коефіцієнти для коливань типу p обчислюють по формулах

	(8.0)
	(8.0)

Якщо резонатор не має втрат, то власна частота ω_p — дійсна, і при частоті збудження ω = ω_p коефіцієнти , і обумовлені ними поля звертаються в нескінченність. Для реального об'ємного резонатора, що володіє втратами, власна частота (ω_р — комплексна. При великих значеннях добротності Q_р об'ємного резонатора власна частота

(8.0)

де Q_p — добротність р-го типу коливань.

З огляду на, що значення Q_p велике, для практичних розрахунків у чисельнику приймають ω_р = ω_р. Тоді

(8.0)

При ω = ω_р коефіцієнти і рівні між собою.

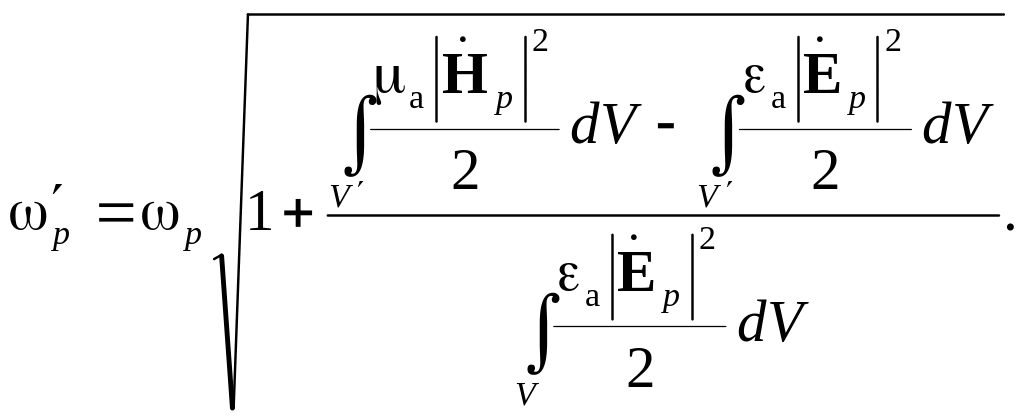
Теорія збурень дозволяє розрахувати зміну власної частоти об'ємного резонатора при деформації його оболонки. Ця деформація може здійснюватися, наприклад, зануренням металевого тіла з обсягом V у резонатор. Власні частоти ω’_р збудженого резонатора можна розрахувати по відомих частотах ω_p і власним векторним функціям Е_р, Н_р незбуреного резонатора:

(8.0)

Тут ,  — максимальна магнітна й електрична енергії коливання в об'ємі V' до введення елемента, що збуджує ; - повна електромагнітна енергія р-й хвилі в резонаторі до введення збурювання. Рівняння ( 8 .0) справедливо при малих деформаціях системи.