Среднее Заочное отделение / 5 семестр / Курсовой ЦМПУ / 5 Раздел 2
.docx2 ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ И ЛОГИЧЕСКОЕ ПРОЕКТИРОВАНИЕ УЗЛОВ УСТРОЙСТВА
2.1 Назначение и принцип построения компараторов четырехразрядных двоичных чисел
Компаратором (устройством сравнения) называется КЦУ, которое предназначено для сравнения двух двоичных чисел. УГО компаратора четырехразрядных двоичных чисел (рисунок 3) представляет собой прямоугольник с абберевиатурой COMP во внутреннем поле (от англ. Comparator).

Рисунок 3 – Условное графическое обозначение четырехразрядного компаратора двоичных чисел
Компаратор имеет две группы входов. На одну из них поступают разряды числа А, на другую группу – разряды числа В.
Появление единичного сигнала на одном из трех выходов компаратора фиксирует результат сравнения. Эти соотношения используются как логические условия (признаки) в микропрограммах, в устройствах автоматического контроля и диагностики и т.д.
В таблице 1 показана связь между сигналами на выходах и входах компаратора при сравнении одноразрядных чисел ai и bi, которые могут быть равны единице или нулю. На соответствующем выходе появляется единичный сигнал, когда в должном соотношении находятся коды на входах. Например, если ai = 1, bi = 1 (числа одинаковы), то функция, характеризующая равенство чисел, FA=B = 1, а функции, характеризующие их неравенство, FA<B = 0 и FA>B = 0. Аналогично заполняются другие строки таблицы.
Таблица 1 – Таблица истинности одноразрядного компаратора
|
Логические аргументы |
Логические функции |
||||
|
ai |
bi |
FA<B |
FA=B |
FA>B |
|
|
0 |
0 |
0 |
1 |
0 |
|
|
0 |
1 |
1 |
0 |
0 |
|
|
1 |
0 |
0 |
0 |
1 |
|
|
1 |
1 |
0 |
1 |
0 |
|
По данным таблицы 1 запишем логические функции для одноразрядного компаратора в СДНФ:
(1)
![]()
Если значения ai и bi таковы, что правые части функций принимают единичные значения, то соотношения, указанные в индексах левых частей, выполняются. Если правые части функций принимают нулевые значения, то соотношения между ai и bi противоположны указанным.
Логическая схема одноразрядного компаратора, реализующая функции (1), приведена на рисунке 4.

Рисунок 4 – Логическая схема одноразрядного компаратора
Остановимся подробнее на равенстве чисел. Заметим, что функция FA=B функция «Равнозначность». По смыслу она противоположна функции FA≠B «Неравнозначность»:
(2)
![]()
Поэтому проверку равенства одноименных разрядов двух чисел можно осуществить, используя логический элемент «Исключающее ИЛИ», дополненный инвертором (рисунок 5).
Когда цифры в одноименных разрядах чисел А и В одинаковы, то на выходах всех логических элементов «Исключающее ИЛИ» нулевые сигналы и функция FA=B = 1. Если хотя бы в одной паре разрядов находятся разные цифры, то на выходе соответствующего логического элемента «Исключающее ИЛИ» единичный сигнал и функция FA=B = 0, что указывает на неравенство чисел А и В.
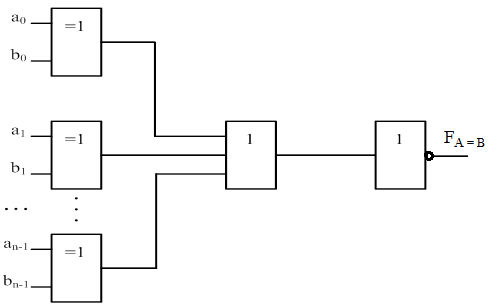
Рисунок 5 – Логическая схема для проверки равенства двух многоразрядных двоичных чисел
Рассмотрим теперь неравенство чисел, используя выражение (1). Пусть А > В. Выявление такого неравенства начинается со старших разрядов; если они равны, то сравнивается следующая пара одноименных разрядов и т.д. Например, в случае трехразрядных чисел могут быть следующие варианты:
-
неравенство цифр в старших разрядах (a2 > b2), что в соответствии с (1) представляется выражением
 .
При этом неравенство чисел А > В
описывается тем же выражением;
.
При этом неравенство чисел А > В
описывается тем же выражением; -
равенство цифр в старших разрядах (a2 = b2), что представляется
выражением
 и неравенство цифр в средних разрядах
(a1
>
b1),
что
описывается выражением
и неравенство цифр в средних разрядах
(a1
>
b1),
что
описывается выражением
 .
При
этом неравенство чисел А > В
представляется
конъюнкцией двух приведенных выражений
.
При
этом неравенство чисел А > В
представляется
конъюнкцией двух приведенных выражений
 ;
;
-
равенство цифр в старших и средних разрядах a2 = b2, a1 = b1, что описывается выражениями
 и
и
 ,
и неравенство цифр в младших разрядах
(a0
>
b0),
что описывается выражением
,
и неравенство цифр в младших разрядах
(a0
>
b0),
что описывается выражением
 .
При этом неравенство чисел А > В
представляется конъюнкциями трех
предыдущих выражений
.
При этом неравенство чисел А > В
представляется конъюнкциями трех
предыдущих выражений
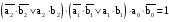 .
.
Поскольку возможен любой из трех вариантов, то выражение, учитывающее все варианты, запишется в виде дизъюнкций приведенных конъюнкций:
(3)
Если на выходе схемы (рисунок 6), элементы которой реализуют выражение (3), устанавливается единичный сигнал, то число А > B.

Рисунок 6 – Логическая схема для проверки неравенства двух
трехразрядных двоичных чисел
На рисунке 7 предыдущая схема дополнена логическим элементом «Исключающее ИЛИ–НЕ» (на входы которого подаются разряды a0, b0), конъюнктором (на выходе которого формируется функция FA=B) и элементом ИЛИ–НЕ (на выходе которого формируется функция FA<B). Если a2 = b2, a1 = b1, a0 = b0, то FA=B = 1, т. е. число А = В. Если в результате сравнения чисел FA>B = 0 и FA=B = 0, то на выходе элемента ИЛИ–НЕ единичный сигнал (FA<B = 1), т. е. число A < B.

Рисунок 7 – Логическая схема трехразрядного компаратора
По аналогичным схемам (см. рисунок 7) строятся компараторы для сравнения двоичных чисел с большей разрядностью.
2.2 Разработка логической схемы счетчика с коэффициентом пересчета Кпер =12
Методику синтеза счетчика на JK-триггерах рассмотрим на примере синтеза логической схемы счетчика с коэффициентом пересчета Kпер = 12 при использовании карт Карно.
Необходимое
число триггеров будет определяться как
минимальное n, удовлетворяющее неравенству
 пер.
В данном случае число триггеров n = 4.
пер.
В данном случае число триггеров n = 4.
В счетчике с коэффициентом пересчета Kпер = 12 двенадцать состояний, причем каждый двенадцатый импульс сбрасывает счетчик в нулевое состояние. Переход счетчика из текущего в следующее состояние связан с переключением триггеров. Для переключения триггеров счетчика в требуемые состояния (таблица 2) на их входах J и K необходимы определенные уровни сигналов. В таблице 3 показаны все возможные переходы состояний триггера и требуемые для этих переходов уровни сигналов на входах J и K. На основании таблицы 3 в таблице 2 указаны уровни сигналов на входах J и K, которые обеспечивают переходы счетчика в следующее состояние.
Таблица 2 – Таблица переходов счетчика с коэффициентом пересчета Kпер = 12, совмещенная с таблицей истинности комбинационных схем возбуждения входов J и K триггеров
|
Номер входного импульса |
Текущее состояние |
Следующее состояние |
Уровни сигналов на входах триггеров |
|||||||||||||||
|
Q3 |
Q2 |
Q1 |
Q0 |
Q3 |
Q2 |
Q1 |
Q0 |
J3 |
K3 |
J2 |
K2 |
J1 |
K1 |
J0 |
K0 |
|||
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
X |
0 |
X |
0 |
X |
1 |
X |
||
|
2 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
X |
0 |
X |
1 |
X |
X |
1 |
||
|
3 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
X |
0 |
X |
X |
0 |
1 |
X |
||
|
4 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
X |
1 |
X |
X |
1 |
X |
1 |
||
|
5 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
X |
X |
0 |
0 |
X |
1 |
X |
||
|
6 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
X |
X |
0 |
1 |
X |
X |
1 |
||
|
7 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
X |
X |
0 |
X |
0 |
1 |
X |
||
|
8 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
X |
X |
1 |
X |
1 |
X |
1 |
||
|
9 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
X |
0 |
0 |
X |
0 |
X |
1 |
X |
||
|
10 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
X |
0 |
0 |
X |
1 |
X |
X |
1 |
||
|
11 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
X |
0 |
0 |
X |
X |
0 |
1 |
X |
||
|
12 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
X |
1 |
0 |
X |
X |
1 |
X |
1 |
||
Таблица 3 – Таблица переходов JK-триггера
|
Вид перехода триггера |
Уровни сигналов на входах |
|
|
J |
K |
|
|
00 |
0 |
X |
|
01 |
1 |
X |
|
10 |
X |
1 |
|
11 |
X |
0 |
|
Примечание – Знак «X» означает произвольный уровень сигнала (0 или 1). |
||
Пусть к моменту подачи первого импульса счетчик находился в состоянии 0000. Под действием этого импульса должно быть обеспечено новое состояние 0001 (таблица 2). Следовательно, в триггере младшего разряда T0 происходит переход вида 01, обеспечиваемый при следующих уровнях на информационных входах: J0 = 1, K0 = X. В остальных триггерах происходит переход вида 00, который обеспечивается уровнями J1 = 0, K1 = X, J2 = 0, K2 = X, J3 = 0, K3 = X. Эти значения занесены в клетки карт Карно для входов J и K всех триггеров, соответствующие состоянию счетчика 0000 (рисунок 2). Пользуясь таблицей 2, можно заполнить карты Карно для входов J и K всех триггеров счетчика. При этом следует помнить, что уровни сигналов на входах J и K являются логическими функциями текущего состояния триггеров и на картах Карно (рисунок 2) под Q3, Q2, Q1, Q0 понимается текущее состояние счетчика, т.е. перед поступлением на вход счетчика очередного импульса. На картах Карно знаком «Ф» обозначены неопределенные значения функций возбуждения входов J и K, соответствующие лишним состояниям счетчика.
Следует помнить, что при минимизации не полностью заданных логических функций произвольные и неопределенные значения функции можно доопределять с целью упрощения результата минимизации. Следовательно, на картах Карно при записи результата минимизации в МДНФ в замкнутые области следует объединять клетки, заполненные единицами, а также произвольными и неопределенными значениями логической функции.
|
|
|
Q1 Q0 |
|
|
|
|
|
|
|
Q1 Q0 |
|
|
|
||||||||||||||||||
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
|
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
||||||||||||||||||
|
|
|
00 |
0 |
0 |
0 |
0 |
|
|
|
|
00 |
Х |
Х |
Х |
Х |
||||||||||||||||
|
J3 : |
01 |
0 |
0 |
1 |
0 |
|
|
K3 : |
01 |
Х |
Х |
Х |
Х |
||||||||||||||||||
|
11 |
Ф |
Ф |
Ф |
Ф |
|
|
11 |
Ф |
Ф |
Ф |
Ф |
||||||||||||||||||||
|
|
|
10 |
Х |
Х |
Х |
Х |
|
|
|
|
10 |
0 |
0 |
1 |
0 |
||||||||||||||||
|
|
|
|
J3=Q0·Q1·Q2 |
|
|
|
|
|
K3=Q0·Q1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Q1 Q0 |
|
|
|
|
|
|
|
Q1 Q0 |
|
|
|
||||||||||||||||||
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
|
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
||||||||||||||||||
|
|
|
00 |
0 |
0 |
1 |
0 |
|
|
|
|
00 |
Х |
Х |
Х |
Х |
||||||||||||||||
|
J2 : |
01 |
Х |
Х |
Х |
Х |
|
|
K2 : |
01 |
0 |
0 |
1 |
0 |
||||||||||||||||||
|
11 |
Ф |
Ф |
Ф |
Ф |
|
|
11 |
Ф |
Ф |
Ф |
Ф |
||||||||||||||||||||
|
|
|
10 |
0 |
0 |
0 |
0 |
|
|
|
|
10 |
Х |
Х |
Х |
Х |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
K2=Q0·Q1 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Q1 Q0 |
|
|
|
|
|
|
|
Q1 Q0 |
|
|
|
||||||||||||||||||
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
|
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
||||||||||||||||||
|
|
|
00 |
0 |
1 |
X |
X |
|
|
|
|
00 |
X |
X |
1 |
0 |
||||||||||||||||
|
J1 : |
01 |
0 |
1 |
X |
X |
|
|
K1 : |
01 |
X |
X |
1 |
0 |
||||||||||||||||||
|
11 |
Ф |
Ф |
Ф |
Ф |
|
|
11 |
Ф |
Ф |
Ф |
Ф |
||||||||||||||||||||
|
|
|
10 |
0 |
1 |
X |
X |
|
|
|
|
10 |
X |
X |
1 |
0 |
||||||||||||||||
|
|
|
|
J1=Q0 |
|
|
|
|
|
K1=Q0 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
Q1 Q0 |
|
|
|
|
|
|
|
Q1 Q0 |
|
|
|
||||||||||||||||||
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
|
|
Q3 Q2 |
|
00 |
01 |
11 |
10 |
||||||||||||||||||
|
|
|
00 |
1 |
X |
X |
1 |
|
|
|
|
00 |
X |
1 |
1 |
X |
||||||||||||||||
|
J0 : |
01 |
1 |
X |
X |
1 |
|
|
K0 : |
01 |
X |
1 |
1 |
X |
||||||||||||||||||
|
11 |
Ф |
Ф |
Ф |
Ф |
|
|
11 |
Ф |
Ф |
Ф |
Ф |
||||||||||||||||||||
|
|
|
10 |
1 |
X |
X |
1 |
|
|
|
|
10 |
X |
1 |
1 |
X |
||||||||||||||||
|
|
|
|
J0=1 |
|
|
|
|
|
K0=1 |
||||||||||||||||||||||
Рисунок 8 – Карты Карно для счетчика с коэффициентом пересчета Kпер = 12
Следует помнить, что при минимизации не полностью заданных логических функций произвольные и неопределенные значения функции можно доопределять с целью упрощения результата минимизации. Следовательно, на картах Карно при записи результата минимизации в МДНФ в замкнутые области следует объединять клетки, заполненные единицами, а также произвольными и неопределенными значениями логической функции.
По картам Карно запишем следующие выражения для функций возбуждения входов J и K всех триггеров счетчика в МДНФ:
 J3=Q0·Q1·Q2; K3=Q0·Q1;
J3=Q0·Q1·Q2; K3=Q0·Q1;
(4) J2=Q0·Q1·Q3; K2=Q0·Q1;
J2=Q0·Q1·Q3; K2=Q0·Q1;
J1=Q0; K1=Q0;
J0=1; K0=1.
Логическая схема счетчика, построенная по логическим функциям (4), представлена на рисунке 9.

Рисунок 9 – Логическая схема счетчика на JK-триггерах с коэффициентом пересчета Kпер = 12
Работа счетчика (рисунок 9) поясняется временными диаграммами, приведенными на рисунке 10 (число входных импульсов N определяется по формуле N = Kпер + 1).

Рисунок 10 – Временные диаграммы работы счетчика с коэффициентом пересчета Kпер = 12
Из временных диаграмм следует, что каждый двенадцатый импульс сбрасывает счетчик в исходное нулевое состояние, а тринадцатый начинает новый цикл работы, повторяющий предыдущий.
2.3 Разработка логической схемы компаратора четырехразрядных двоичных чисел в основном базисе
Логическую схему четырехразрядного компаратора двоичных чисел разработаем в основном базисе. Для этого на основании логических функций (1)…(3) запишем логические функции для выходов четырехразрядного компаратора.
Используя выражение (1) запишем вариант неравенства А > В четырехразрядного числа для каждого разряда отдельно:

 ;
;
(5) ;
;
 ;
;
 .
.
Используя все варианты из выражения (5) выведем формулу, определяющую неравенство двух четырехразрядных чисел:
(6)


Однако если все разряды числа будут равны, то выражение будет записано следующим образом:
(7)
В противном случае:
(8)

Построим логическую схему четырехразрядного двоичного компаратора в основном базисе (лист 1).
Проверим правильность функционирования данной логической схемы. Для этого на входы подадим числа A = 1000(2) и В = 1011(2), где а3 = 1, а2 = 0, а1 = 0, а0 = 0, b3 = 1, b2 = 0, b1 = 1, b0 = 1.
Таким образом, на выходе получили результат: FA>B = 0, FA<B = 1, FA=B = 0. Следовательно, A < B, т.е. 1000(2) < 1011(2).









 J2=Q0·Q1·Q3
J2=Q0·Q1·Q3