Геометрический метод расчета
Геометрическое решение можно найти используя преобразованную плоскость решений.
Рис.8 – Исходная плоскость множества решений
Решение на плоскости ищется следующим образом:
Шаг 1.
Строится новая плоскость решений, где осями будут не и , а и . На этой плоскости строятся точки соответствующие решениями.
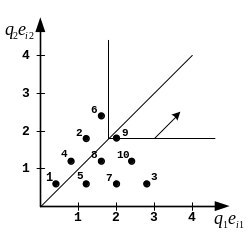
Рис.9 – Новая плоскость множества решений
Шаг 2.
Строится направляющая –линия проведенная из начала координат под углом 45
Шаг 3.
Линия, соответствующая критерию (прямой угол) движется вдоль направляющей от начала координат до касания последней точки, которая и будет решением. В данном случае точка с координатами (2; 1,2), т.е. E9
Критерий произведений
Математическая интерпретация
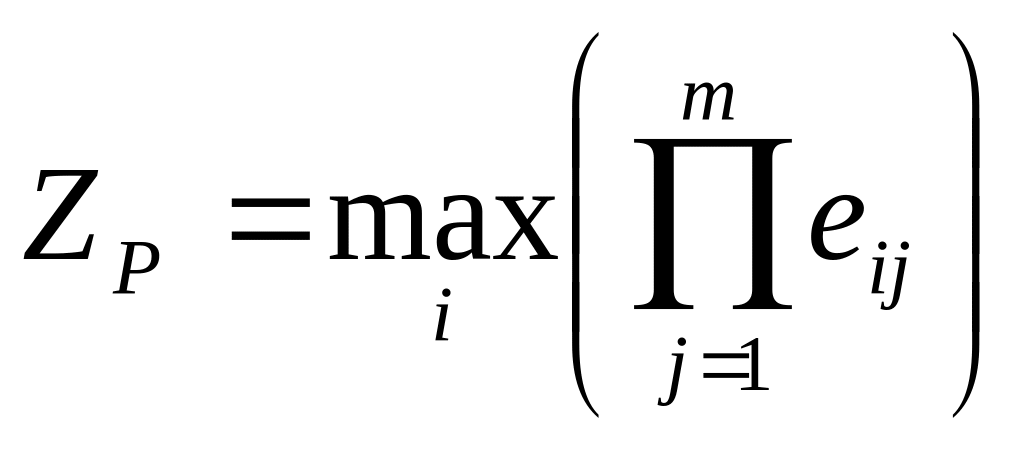
Аналитический метод расчета
Дана матрица решений:
|
F1 |
F2 |
E1 |
1 |
1 |
E2 |
3 |
3 |
E3 |
7 |
1 |
E4 |
2 |
2 |
E5 |
3 |
1 |
E6 |
4 |
4 |
E7 |
5 |
1 |
E8 |
4 |
2 |
E9 |
5 |
3 |
E10 |
6 |
2 |
Шаг 1. Находим произведение и
|
F1 |
F2 |
|
E1 |
1 |
1 |
1 |
E2 |
3 |
3 |
9 |
E3 |
7 |
1 |
7 |
E4 |
2 |
2 |
4 |
E5 |
3 |
1 |
3 |
E6 |
4 |
4 |
16 |
E7 |
5 |
1 |
5 |
E8 |
4 |
2 |
8 |
E9 |
5 |
3 |
15 |
E10 |
6 |
2 |
12 |
Шаг 2. Находим максимум в последнем столбце.
|
F1 |
F2 |
|
E1 |
1 |
1 |
1 |
E2 |
3 |
3 |
9 |
E3 |
7 |
1 |
7 |
E4 |
2 |
2 |
4 |
E5 |
3 |
1 |
3 |
E6 |
4 |
4 |
16 |
E7 |
5 |
1 |
5 |
E8 |
4 |
2 |
8 |
E9 |
5 |
3 |
15 |
E10 |
6 |
2 |
12 |
|
|
|
16 |
Оптимальное решение: Все решения для которых максимально. В нашем случае это E6