Критерий Байеса–Лапласа Аналитический метод расчета
Математическая интерпретация критерия выглядит следующим образом:
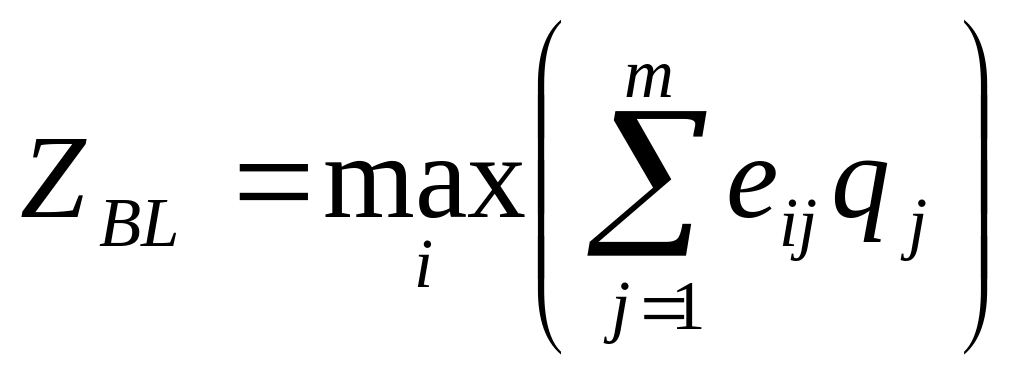
где qj – вероятности условий. Если qj не заданы, то считаем, что условия равновероятны: q1 = q2 = 0,5.
Процесс нахождения оптимального решения рассмотрим на примере.
Заданная матрица решений:
|
F1 |
F2 |
E1 |
1 |
1 |
E2 |
3 |
3 |
E3 |
7 |
1 |
E4 |
2 |
2 |
E5 |
3 |
1 |
E6 |
4 |
4 |
E7 |
5 |
1 |
E8 |
4 |
2 |
E9 |
5 |
3 |
E10 |
6 |
2 |
Шаг 1.
Находим
произведение
и
соответствующей вероятности
в каждой
строке.
|
F1 |
F2 |
|
|
E1 |
1 |
1 |
0,5 |
0,5 |
E2 |
3 |
3 |
1,5 |
1,5 |
E3 |
7 |
1 |
3,5 |
0,5 |
E4 |
2 |
2 |
1 |
1 |
E5 |
3 |
1 |
1,5 |
0,5 |
E6 |
4 |
4 |
2 |
2 |
E7 |
5 |
1 |
2,5 |
0.5 |
E8 |
4 |
2 |
2 |
1 |
E9 |
5 |
3 |
2,5 |
1.5 |
E10 |
6 |
2 |
3 |
1 |
Шаг 2.
Находим сумму значений и для каждой строки
|
F1 |
F2 |
|
|
|
E1 |
1 |
1 |
0,5 |
0,5 |
1 |
E2 |
3 |
3 |
1,5 |
1,5 |
3 |
E3 |
7 |
1 |
3,5 |
0,5 |
4 |
E4 |
2 |
2 |
1 |
1 |
2 |
E5 |
3 |
1 |
1,5 |
0,5 |
2 |
E6 |
4 |
4 |
2 |
2 |
4 |
E7 |
5 |
1 |
2,5 |
0.5 |
3 |
E8 |
4 |
2 |
2 |
1 |
3 |
E9 |
5 |
3 |
2,5 |
1.5 |
4 |
E10 |
6 |
2 |
3 |
1 |
4 |
|
|
|
|
|
4 |
Шаг 3.
Находим максимальное значение в добавленном столбце .
Соответственно оптимальными решениями являются все решения, значения которых равны 4. В данном случае имеем четыре решения – E3, E6, E9, E10.