
Среднее Заочное отделение / 4 семестр / Цифровые и микропроцессорные устройства / Электронный конспект лекций (ЦиМПУ)
.pdf2.1.5 Преобразователи кодов
Преобразователем кодов (ПК) называют КЦУ, которое преобразует n-разрядные двоичные входные слова в m-разрядные двоичные выходные слова. Иногда ПК называют n, m-преобразователями. Рассмотренные ранее дешифраторы и шифраторы являются ПК некоторых частных видов, например, их можно использовать для преобразования чисел из одной позиционной системы счисления в другую.
Для представления информации в цифровых устройствах используются двоичные коды. Например, двоично-десятичный код 8421 (BCD-код) используется для представления десятичных чисел. Двоично-десятичный код с избытком 3, также используемый для представления десятичных цифр, образуется от соответствующих представлений цифр в коде 8421 путем прибавления двоичного числа 0011. Код с избытком 3 является самодополняющим кодом. Правила преобразования прямого кода с избытком 3 в дополнительный с избытком 3 и правила обратного преобразования такие же, как и для двоичного дополнительного кода. Поэтому код с избытком 3 удобнее использовать для выполнения арифметических операций.
Построение схемы ПК рассмотрим на конкретном примере. Пусть требуется построить преобразователь четырехразрядных двоично-десятичных цифр из кода 8421 в код с избытком 3. УГО такого ПК представлено на рисунке 2.9.
x0 |
|
1 |
X/Y 0 |
|
y0 |
|
|
||||
x1 |
|
2 |
1 |
|
y1 |
|
|
||||
|
|||||
x2 |
|
4 |
2 |
|
y2 |
|
|
||||
x3 |
|
8 |
3 |
|
y3 |
|
|
Рисунок 2.9 – Условное графическое обозначение преобразователя кода 8421 в код с избытком 3
Соотношение входных и выходных слов задано таблицей истинности (таб-
лица 2.3).
101

Таблица 2.3 – Таблица истинности преобразователя кода 8421 в код с избытком 3
|
Логические аргументы |
|
Промежуточная пе- |
|
Логические функции |
|
||||||
|
|
ременная |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
x2 |
x1 |
|
x0 |
zi |
y3 |
|
y2 |
y1 |
|
y0 |
0 |
|
0 |
0 |
|
0 |
z0 |
0 |
|
0 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
0 |
|
1 |
z1 |
0 |
|
1 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
0 |
z2 |
0 |
|
1 |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
1 |
|
1 |
z3 |
0 |
|
1 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
|
0 |
z4 |
0 |
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
0 |
|
1 |
z5 |
1 |
|
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
1 |
|
0 |
z6 |
1 |
|
0 |
0 |
|
1 |
0 |
|
1 |
1 |
|
1 |
z7 |
1 |
|
0 |
1 |
|
0 |
1 |
|
0 |
0 |
|
0 |
z8 |
1 |
|
0 |
1 |
|
1 |
1 |
|
0 |
0 |
|
1 |
z9 |
1 |
|
1 |
0 |
|
0 |
Имея таблицу истинности, можно использовать три подхода к синтезу ПК:
–преобразователь синтезируется как однокомпонентная минимизированная комбинационная схема с нерегулярной структурой (по общим правилам синтеза КЦУ);
–преобразователь синтезируется как слабо минимизированная комбинационная схема с частично регулярной структурой (на основе шифратора и дешифратора);
–преобразователь синтезируется как неминимизированная комбинационная схема с регулярной структурой (на основе постоянного запоминающего устройства).
Рассмотрим первый традиционный подход. По данным таблицы 2.3 заполним карты Карно (рисунок 2.10).
X1 X0 |
|
|
|
|
X3 X2 |
00 |
01 |
11 |
10 |
|
|
|
|
|
00 |
0 |
0 |
0 |
0 |
01 |
0 |
1 |
1 |
1 |
11 |
Ф |
Ф |
Ф |
Ф |
10 |
1 |
1 |
Ф |
Ф |
y3 = x3 ˅ x0 · x2 ˅ x1 · x2.
X1 X0 |
|
|
|
|
X3 X2 |
00 |
01 |
11 |
10 |
|
|
|
|
|
00 |
0 |
1 |
1 |
1 |
01 |
1 |
0 |
0 |
0 |
11 |
Ф |
Ф |
Ф |
Ф |
10 |
0 |
1 |
Ф |
Ф |
y2 = x0 · x1 · x2 ˅ x0 · x2 ˅ x1 · x2.
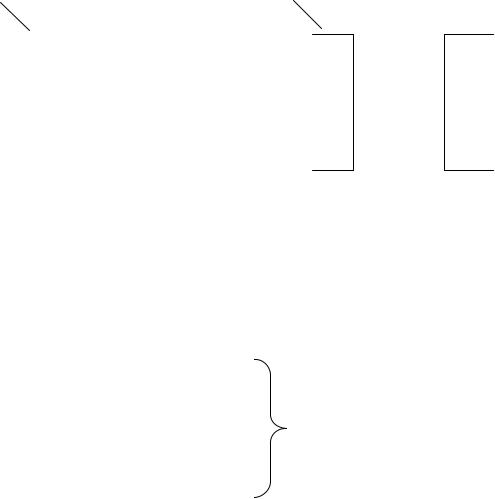
Рисунок 2.10 – Карты Карно для преобразователя кода 8421 в код с избытком 3
102
X1 |
X0 |
|
|
|
|
|
|
|
X1 |
X0 |
|
|
|
|
X3 X2 |
00 |
01 |
11 |
10 |
|
X3 X2 |
00 |
01 |
11 |
10 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
00 |
1 |
|
0 |
|
1 |
0 |
|
00 |
1 |
0 |
0 |
|
1 |
|
01 |
1 |
|
0 |
|
1 |
0 |
|
01 |
1 |
0 |
0 |
|
1 |
|
11 |
Ф |
Ф |
|
Ф |
Ф |
|
11 |
Ф |
Ф |
Ф |
Ф |
|||
10 |
1 |
|
0 |
|
Ф |
Ф |
|
10 |
1 |
0 |
Ф |
Ф |
||
|
y |
= x |
· x |
˅ x |
· x |
. |
|
|
y |
= x |
. |
|
||
|
1 |
|
0 |
|
1 |
0 |
1 |
|
|
|
0 |
0 |
|
|
Окончание рисунка 2.10
Выполним соответствующие объединения заполненных клеток на рисунке 2.10 с учетом неопределенностей и запишем результаты минимизации в МДНФ:
y |
3 |
= x |
3 |
˅ x |
0 |
· x |
2 |
˅ x |
1 |
· x |
; |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||||
y |
2 |
= x |
0 |
· x |
1 |
· x |
2 |
˅ x |
0 |
|
· x |
2 |
˅ x |
1 |
· x |
; |
|||
|
|
|
|
|
|
|
|
2 |
|
||||||||||
y |
|
= x |
|
· x |
|
|
˅ x |
|
· x |
|
|
; |
|
|
|
|
(2.7) |
||
1 |
0 |
1 |
0 |
1 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
y |
0 |
= x |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
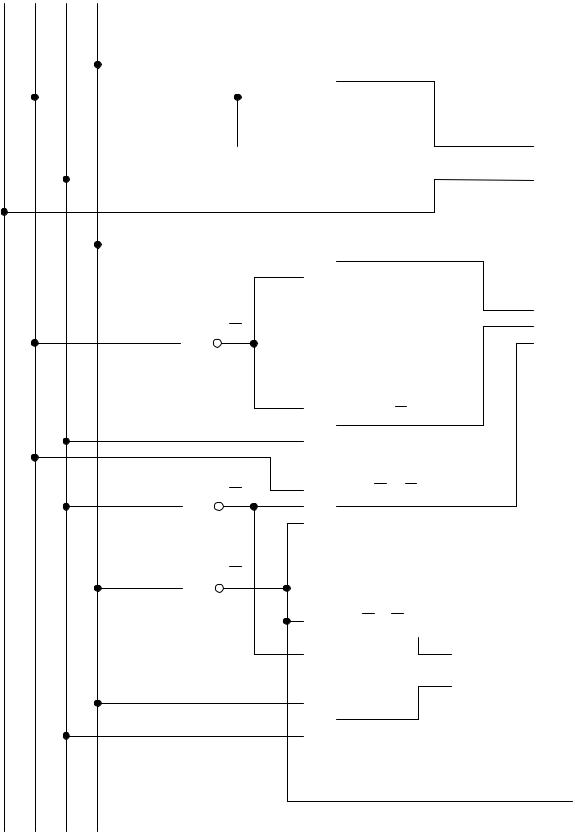
Далее по функциям системы (2.7) методом прямого замещения построим логическую схему ПК в основном базисе (рисунок 2.11).
На рисунке 2.11 проведена проверка правильности функционирования схемы для входного слова 0011. Так как на выходах схемы установилось выходное слово 0110, то ПК функционирует в соответствии с таблицей 2.3.
Кдостоинству первого подхода относится экономичность синтезируемой схемы по аппаратурным затратам, исчисляемым в условных транзисторах. Это означает, что схема будет занимать небольшую часть площади кристалла. Оценка схемы на рисунке 2.11 дает величину ЕПК (1) = 26 условных транзистора.
Кнедостатку этого подхода можно отнести то, что схема получилась нерегулярной (с неравным числом конъюнкторов в цепи каждого выхода, с перекрещивающимися связями), что делает ее нетехнологичной при изготовлении.
103
X3 X2 X1 |
X0 |
||||
0 |
0 |
1 |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 X2
1
1 X1
0
1 X0
0
& |
X0 |
· X2 |
|
|
|
||
|
|
|
|
||||
|
0 |
|
|
|
|
|
|
& |
X1 |
· X2 |
1 |
0 |
|
||
|
|
y3 |
|||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
X0 |
· X2 |
|
|
|
|||
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
1 |
1 |
|
|
y2 |
|
|
|
&X1 · X2 1
&X0 · X1 · X2
0
&X0 · X1
|
0 |
|
1 |
|
|
|
|
1 |
|
||
|
|
|
|
y1 |
|
& |
X0 |
· X1 |
|
||
|
|
||||
|
|
|
|||
|
1 |
|
|
|
|
0 |
y0 |
|
Рисунок 2.11 – Логическая схема ПК 8421 в код с избытком 3 в основном базисе
Второй подход позволяет повысить регулярность структур ПК за счет некоторого увеличения аппаратурных затрат. Исходная информация для синтеза в
104

этом случае также содержится в таблице 2.3, в которой имеется столбец с промежуточной переменной zi (при первом подходе этот столбец не учитывался).
Левая и центральная части таблицы 2.3 представляют собой описание дешифратора, а правая и центральная части представляют собой таблицу кодирования некоторого шифратора. Таким образом, схема ПК в данном случае приобретает двухкомпонентную структуру вида «десятичный дешифраторшифратор» (рисунок 2.12). Она несколько сложнее схемы на рисунке 2.11 (ЕПК(2)=77 условных транзисторов), но значительно проще для обозрения.
К недостатку полученной схемы следует отнести ее специализированность, что снижает массовость выпуска подобных схем и приводит к относительно высокой цене изделия.
x |
1 |
DC |
0 |
0 |
CD |
0 |
y |
0 |
|
|
|
|
|
|
0 |
|
|
|
1 |
1 |
|
|
|
|
|
|
2 |
2 |
|
|
|
x |
2 |
|
3 |
3 |
|
1 |
y |
1 |
|
|
|
|
|
|
1 |
|
|
|
4 |
4 |
|
|
|
|
|
|
5 |
5 |
|
|
|
x |
4 |
|
6 |
6 |
|
2 |
y |
2 |
|
|
|
|
2 |
||
|
|
|
7 |
7 |
|
|
|
x |
8 |
|
8 |
8 |
|
3 |
y |
|
|
|
|
||||
3 |
|
|
9 |
9 |
|
|
3 |
|
|
|
|
|
|
Рисунок 2.12 – Преобразователь кода с частично регулярной структурой
Третий подход позволяет значительно повысить регулярность структуры ПК и одновременно существенно расширить его функциональные возможности. В этом случае запрещается использовать специализированные компоненты, например, десятичный дешифратор. Таким образом, ПК должен содержать полный двоичный n-входной дешифратор и 2n-входной шифратор. В результате получается постоянное запоминающее устройство (ПЗУ). Следовательно, ПЗУ
– это n, m-преобразователь с двухкомпонентной регулярной структурой, на выходе которого включен шифратор, формирующий m-разрядные слова.
Входное слово ПК в этом случае является адресом ячейки ПЗУ, в которой хранится соответствующее выходное слово. УГО ПК на ПЗУ представлено на рисунке 2.13. Оно представляет собой прямоугольник с n-входами и m-
105

выходами, во внутреннем поле которого записана аббревиатура ROM (от англ.
Read Only Memory).
x0 |
ROM |
y |
|
|
0 |
x |
|
y |
1 |
|
|
|
|
1 |
x |
|
y |
2 |
|
2 |
|
|
|
x |
|
y |
3 |
|
3 |
Рисунок 2.13 – Преобразователь кода на основе ПЗУ
2.1.6 Мультиплексоры
Мультиплексором называется КЦУ, которое обеспечивает альтернативную (поочередную) передачу данных от нескольких источников одному приемнику. Эта операция коммутации каналов называется мультиплексированием. Если требование альтернативности отсутствует, то задача мультиплексирования вырождается в случай логического сложения данных. При m источниках информации мультиплексор должен иметь m информационных входов, k ≥ log2m адресных входов и один информационный выход. Разрядности каналов передачи могут быть различными, мультиплексоры для коммутации многоразрядных слов составляются из одноразрядных.
Принцип построения одноразрядных мультиплексоров рассмотрим на примере синтеза мультиплексора на четыре информационных входа (m=4). УГО такого мультиплексора (рисунок 2.14) представляет собой прямоугольник с аббревиатурой MUX (от англ. Multiplexer) во внутреннем поле.
x |
I |
MUX |
|
|
|
|
|||
|
0 |
|
|
|
x |
0 |
|
|
|
I |
|
|
||
|
1 |
|
|
|
x |
|
1 |
|
|
|
I |
|
|
|
2 |
|
|
||
x |
|
2 |
Y |
y |
3 |
I |
|||
a0 |
3 |
|
|
|
A |
|
|
||
a |
|
0 |
|
|
|
A |
|
|
|
1 |
|
|
||
|
|
1 |
|
|
Рисунок 2.14 – Условное графическое обозначение одноразрядного мультиплексора для m=4
Входы А1, А0 служат для приема адреса источника, от которого подается информация в данный момент.
106

По приведенному описанию составим таблицу истинности для мультиплексора (таблица 2.4).
Таблица 2.4 – Таблица истинности одноразрядного мультиплексора для m=4
|
|
Логические аргументы |
|
Логическая |
|||
|
|
|
функция |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
x1 |
|
x2 |
x3 |
а1 |
а0 |
y |
|
|
|
|
|
|
|
|
0 |
x |
|
x |
x |
0 |
0 |
0 |
1 |
x |
|
x |
x |
0 |
0 |
1 |
|
|
|
|
|
|
|
|
x |
0 |
|
x |
x |
0 |
1 |
0 |
x |
1 |
|
x |
x |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
x |
x |
|
0 |
x |
1 |
0 |
0 |
x |
x |
|
1 |
x |
1 |
0 |
1 |
|
|
|
|
|
|
|
|
x |
x |
|
x |
0 |
1 |
1 |
0 |
x |
x |
|
x |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
Из таблицы 2.4 следует, что сигнал на выходе y является логической функцией шести аргументов.
Запишем логическую функцию для выхода мультиплексора в СДНФ:
y x |
0 |
a a |
0 |
x |
a |
a |
0 |
x |
2 |
a a |
0 |
x |
3 |
a |
a |
0 |
. |
||
|
1 |
|
1 |
1 |
|
|
1 |
|
|
1 |
|
|
|||||||
Логическая схема мультиплексора, построенная |
|
||||||||||||||||||
приведена на |
|
рисунке |
2.15, |
а |
(штриховой |
линией |
|
||||||||||||
(2.8)
по функции (2.8), показаны цепи для
организации входа разрешения работы |
EN |
). |
|
|
|
Схема получилась экономичной |
по аппаратурным затратам (ЕMUX = 20 |
|
условных транзисторов), достаточно быстродействующей (TMUX = 4 tзд. ЛЭ), но плохо структурированной.
Для структурирования схемы мультиплексора представим функцию (2.8) в виде:
y x |
0 |
z |
0 |
x |
z |
x |
2 |
z |
2 |
x |
3 |
z |
, |
|
|
1 |
1 |
|
|
|
3 |
|
где z0 = a1 ∙ a0; z1 = a1 ∙ a0; z2 = a1 ∙ a0; z3 = a1 ∙ a0.
(2.9)
(2.10)
В этом случае в схеме мультиплексора (рисунок 2.15, б) выделяются два структурных компонента: управляемый коммутатор, описываемый функцией (2.9), и управляющий дешифратор, описываемый системой функций (2.10). Аппаратурные затраты на реализацию структурированного варианта мультиплексора
107
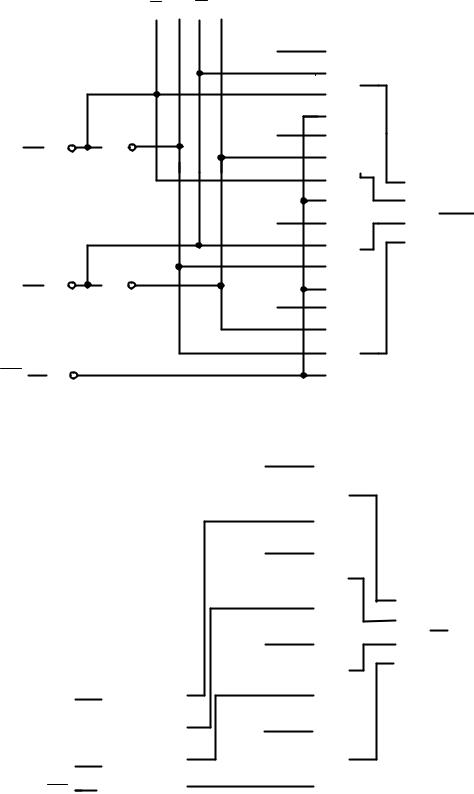
составляют 24 условных транзистора, а быстродействие оценивается величиной 5
tзд. ЛЭ.
|
|
|
|
|
|
а |
а |
1 |
а |
а |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
0 |
1 |
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
0 |
1 |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
а |
|
1 |
1 |
|
1 |
|
|
|
|
|
x1 |
0 |
& |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
2 |
y |
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
& |
|
||
|
|
|
|
|
|
|
|
|
|
|
2 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
а |
0 |
0 |
1 |
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
0 |
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
EN |
0 |
1 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 |
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
z0 |
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
z1 |
|
0 |
|
|
1 |
|
||
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
& |
x2 |
x2y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
0 |
1 |
DC |
0 |
|
0 |
z2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
1 |
|
0 |
|
x3 |
|
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a1 |
1 |
2 |
|
2 |
|
1 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
EN |
|
3 0 z3 |
|
|
|
|
|
|||||
|
|
|
EN |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б)
Рисунок 2.15 – Одноразрядный мультиплексор для m=4. Логическая схема неструктурированная (а) и структурированная (б)
108
В сериях интегральных микросхем стандартной логики, представлены мультиплексоры с числом информационных входов m = 2,4,8,16. Например, микросхема 1554КП16 содержит четыре мультиплексора «2-1» со стробированием. Для наращивания числа информационных входов строят пирамидальную структуру из нескольких мультиплексоров с меньшим числом информационных входов, называемую мультиплексорным деревом. При этом первый ярус схемы представляет собой столбец, содержащий столько мультиплексоров, сколько необходимо для получения нужного числа информационных входов m. Все мультиплексоры столбца адресуются младшими разрядами k1 общего адресного кода (k1 = log2m1, где m1 – число информационных входов мультиплексоров первого яруса). Старшие разряды адресного кода, число которых равно k - k1 (k = log2m, где m - общее число информационных входов мультиплексорного дерева), используются во втором ярусе, мультиплексор которого обеспечивает поочередную работу мультиплексоров первого яруса на общий выходной канал.
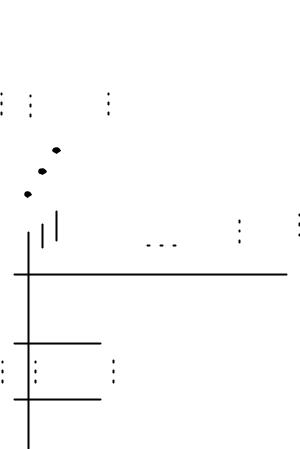
Схема мультиплексорного дерева на 32 информационных входа на основе мультиплексоров на 8 информационных входов показана на рисунке 2.16.
|
|
|
|
|
|
|
|
|
MUX1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 0 |
|
|
|
|
I 0 |
MUX |
|
|
|
|
|
|
||||
|
|
|
|
8-1 |
|
|
|
|
|
|
|
|||||
x1 |
|
|
|
|
I 1 |
Y |
x1 |
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x7 |
|
|
|
|
I |
7 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
A0 |
|
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
MUX5 |
|
|
|||||
a1 |
|
|
|
A1 |
|
|
|
|
|
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
||||||
a |
2 |
|
|
|
A |
|
|
|
|
|
MUX |
|
|
|||
|
|
|
|
|
|
2 |
|
|
|
|
I 0 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
4-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
I 3 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Y |
25 |
y |
a3 |
|
|
|
|
|
|
MUX4 |
|
|
A0 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
a |
|
1 |
|
|
|
|
|
|
|
|
A |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x24 |
|
|
|
|
I0 |
MUX |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||||||
x25 |
|
|
|
I1 |
8-1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
x25 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||||||
x31 |
|
|
|
I 7 |
Y |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
A0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
A2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рисунок 2.16 – Схема наращивания числа информационных входов мультиплексора
109

Три младших разряда адреса а2, а1, а0 подаются на адресные входы мультиплексоров первого яруса, а два старших разряда а4 и а3 – на адресные входы мультиплексора второго яруса. Например, адресный код 11001(2)=25(10) обеспечивает коммутацию выхода схемы с информационным входом x25 (рисунок 2.16).
Как отмечалось выше, универсальные логические модули (УЛМ) на основе мультиплексоров можно использовать для схемотехнической реализации различных логических функций. Универсальность их состоит в том, что для заданного числа аргументов можно настроить УЛМ на любую функцию. Для использования мультиплексора в качестве УЛМ следует изменить назначение его входов. На адресные входы следует подавать аргументы функции, а на информационные входы
– сигналы настройки. Действительно, каждому набору аргументов соответствует передача на выход одного из сигналов настройки. Если этот сигнал является значением функции на данном наборе аргументов, то задача решена.
На рисунке 2.17 показан пример воспроизведения функции неравнозначности у = x1 x2 с помощью мультиплексора «4-1» при настройке УЛМ константами.
0 |
I |
|
MUX |
0 |
4-1 |
||
1 |
I |
|
|
1 |
|
I 2 |
Y |
|
y = x1+ x2 |
|
I |
3 |
|
||
|
|
|
||
x2 A0 x1 A1
Рисунок 2.17 – Схема реализации неравнозначности при настройке УЛМ константами
Большое число настроечных входов затрудняет реализацию УЛМ. Для УЛМ, расположенных внутри кристалла, можно вводить код настройки последовательно в регистр сдвига, к разрядам которого подключены входы настройки. Тогда будет только один внешний вход настройки, но настройка будет занимать не один, а 2n тактов (где n – число аргументов). Существуют и другие более сложные способы настройки УЛМ.
110
