Реализация задачи Эйнштейна в модели ООП

•Программный модуль состоит из двух основных частей: набора классов, реализующих фреймовую модель, и внешнего модуля, который осуществляет генерацию наборов данных, наблюдение за «реакцией» модели и принятие необходимых решений.

•Вся предметная область разбита на пять уровней иерархии:

1) уровень домов → 2) уровень людей → 3) уровень напитков → 4) уровень растений → 5) уровень животных.

•Такой порядок следования уровней означает, что сначала определяется позиция дома, затем для данного дома определяется его жилец, после чего для жильца определяются его напиток, растение и животное. В общем случае порядок уровней не играет решающей роли, но для конкретной реализации он должен быть фиксирован.

Диаграммы классов предметной области задачи Эйнштейна

Реализация задачи Эйнштейна в модели ООП (осуществление перебора вариантов, откат в случае несоответствия генерируемой перестановки условию задачи)

•Программа действует методом проб и ошибок. На самом верхнем уровне генерируется перестановка домов. Каждому дому присваивается позиция, соответствующая его номеру в перестановке.

•При этом программа наблюдает за «реакцией» модели. Допустим, что в перестановке зеленый дом оказался справа от белого (по условию, зеленый дом стоит слева от белого). При присвоении зеленому дому его позиции он проверит, где в данный момент находится белый дом. Если позиция белого дома уже определена, и он не стоит слева от зеленого, объект, представляющий зеленый дом, выбросит исключение, сигнализирующее о том, что произошел конфликт с условием задачи. Внешняя программа перехватит исключение, произведет откат перестановки на текущем уровне (обнулит позиции всех домов) и перейдет к генерации следующей перестановки.

Реализация задачи Эйнштейна в модели ООП (переход на нижележащий уровень иерархии)

•Если текущая перестановка не вызвала конфликт условий, программа спустится на уровень ниже.

•На следующем уровне генерируется перестановка людей. После генерации каждому человеку присваивается дом из текущей перестановки домов, номер которого соответствует номеру данного человека в перестановке людей. При этом модель автоматически присваивает значения определенным атрибутам объектов в соответствии с условиями задачи.

•Допустим, внешняя программа пытается «поселить» датчанина в желтый дом, стоящий на позиции «3». Объект, представляющий датчанина, проверяет позицию желтого дома и, обнаружив, что дом стоит посередине, присваивает атрибуту «напиток» значение «молоко», т.к. по условию жилец из среднего дома пьет молоко. При этом этот же объект проверяет, не связано ли молоко с каким-либо другим человеком. Если оказывается, что молоко уже используется для кого-то в качестве напитка, генерируется исключение. Таким образом, модель самостоятельно проверяет соблюдение всех условий задачи. Внешней программе остается лишь генерировать перестановки и следить за реакцией модели.

Реализация задачи Эйнштейна в модели ООП (временная сложность решения задачи)

•Предметная область задачи состоит из 5 уровней по 5 объектов в каждом, т.е. количество всех возможных перестановок составляет (5!)5 = 24 883 200 000.

•Для каждого уровня существуют условия, которые позволяют «забраковать» перестановку еще до спуска на уровень ниже. Для уровня домов это условие «Зеленый дом стоит слева от белого», которое сразу отбрасывает больше половины всех возможных перестановок домов. На уровне людей имеются 2 условия: «Англичанин живет в красном доме» и «Норвежец живет в первом доме». Можно показать, что уже после применения условий для 1-го и 2-го уровней, от исходных 25 миллиардов остаются не более 500 миллионов перестановок, проверка которых требует спуска на нижние уровни модели.

Понятие «система фреймов»

•Группа фреймов может объединяться в систему фреймов. Результаты характерных действий отражаются с помощью трансформаций между фреймами системы. Они используются, чтобы ускорить вычисления определенных видов при представлении типичных изменений одной и той же ситуации.

•В случае зрительного образа различные фреймы системы описывают картину с различных точек наблюдения, а трансформация одного фрейма в другой отражают результаты перемещения из одного места в другое. Для фреймов невизуальных видов различия между фреймами системы могут отражать действия, причинно-следственные связи и изменения понятийной точки зрения.

•Различные фреймы системы используют одни и те же слоты-терминалы. Благодаря этому экономится объем памяти ЭВМ, используемой для построения модели реального мира.

Понятие «система фреймов» - задания отсутствия

•Характерной чертой подхода с использованием фреймов является возможность использования различных видов прогнозов, ожиданий, предположений. В соответствии с этим слоты- терминалы фрейма, выбираемого для представления ситуации, обычно уже заполнены заданиями, которые наиболее вероятны в данной ситуации. Эти задания называются "заданиями отсутствия".

•Таким образом, фрейм может содержать большое число деталей, которые могут и не подтвердиться данной ситуацией. Задания отсутствия "непрочно" связаны со своими терминалами, поэтому они могут быть легко "вытеснены" другими заданиями, которые лучше подходят к текущей ситуации.

•После того как выбран фрейм для представления ситуации, процесс согласования фрейма с данной конкретной ситуацией состоят в нахождении таких заданий для терминалов фрейма, которые совместимы с маркерами терминалов. Процесс согласования частично контролируется информацией, связанной с фреймом (в которую входит и информация относительно того, как действовать в случае появления необычных ситуаций, "сюрпризов"), а частично знанием текущих целей.

Фрейм - визуальный образ

В качестве простейшего примера рассмотрим приведенную в работе М.Минского возможную систему фреймов для элементарного зрительного образа - куба. Можно допустить, что результатом разглядывания куба является структура, подобная показанной на рис.П1а. Эту структуру можно идентифицировать с фреймом куба при разглядывании его с соответствующей позиции. Области A, E и B являются терминалами фрейма, задания для которых соответствуют возможным деталям или обозначениям на видимых с данной позиции гранях куба.

Фрейм - визуальный образ

Если позиция наблюдения куба перемещается вправо, то грань А исчезает из поля зрения и становится видимой грань С.

Если бы потребовалось провести полный анализ этого нового визуального образа, необходимо было бы:

1)утратить знания о грани А,

2)повторно воспринять (с помощью соответствующих "вычислений") образ грани В,

3)воспринять образ новой грани С.

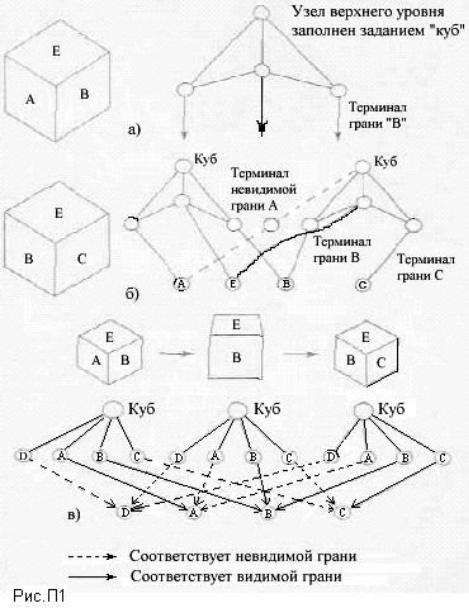
Фрейм - визуальный образ

Однако, поскольку известно, что произошло перемещение позиции наблюдения вправо, можно сохранить знания о грани В в виде задания терминалу левой грани нового фрейма куба, соответствующего новой позиции наблюдения. Кроме того, чтобы сохранить знания и о грани А, можно ввести дополнительный терминал невидимой грани, относящийся к этому новому фрейму, как это показано на рис.П1б.

При возвращении на начальную позицию наблюдения оказывается возможным восстановить визуальный образ куба без каких-либо новых "вычислений". Для этого достаточно "вызвать" из памяти первый фрейм. Полезно сохранить знания и о грани С, для чего можно ввести дополнительный терминал этой невидимой грани в первом фрейме (рис.П1б).